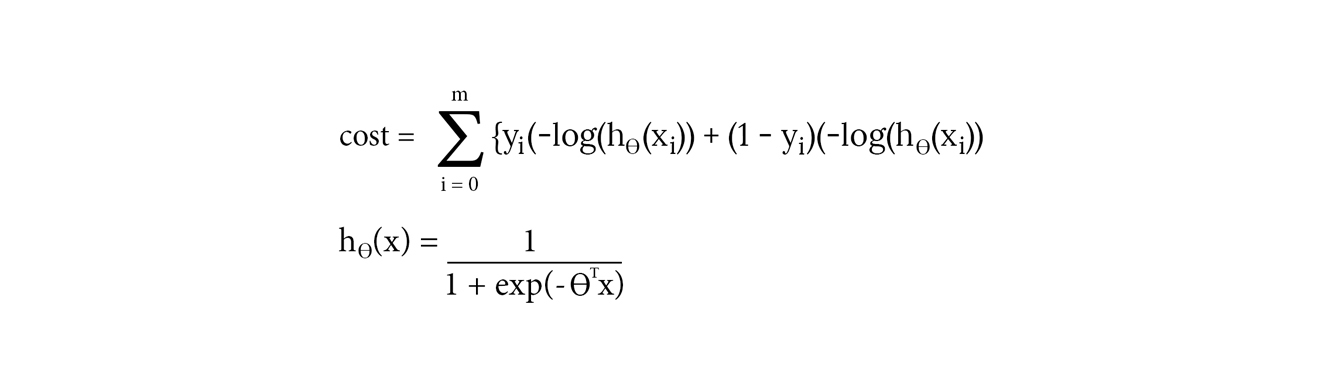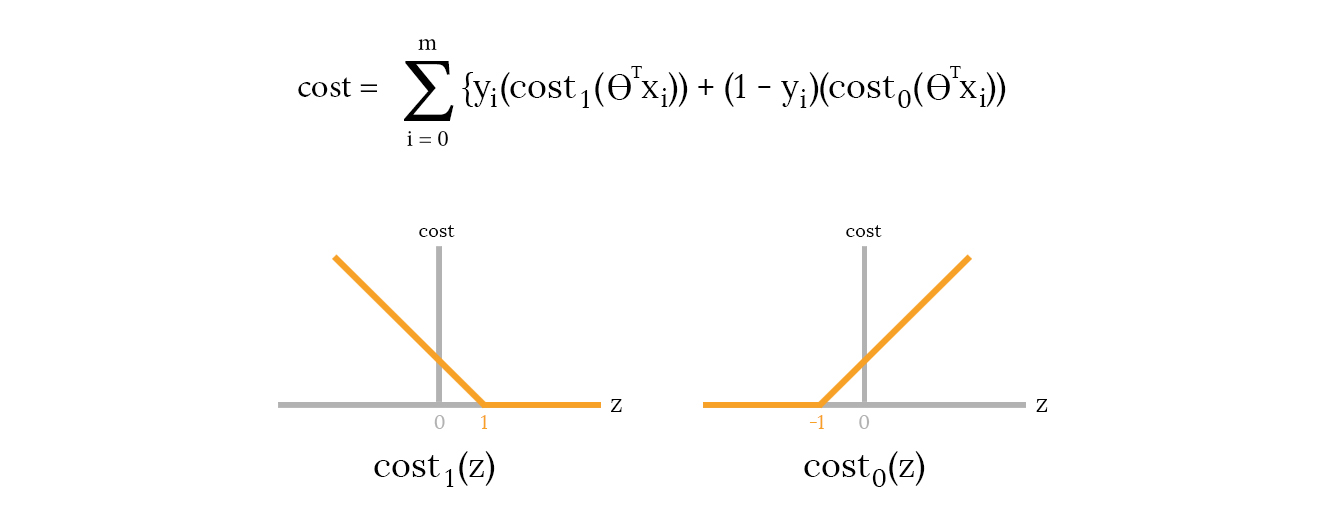Implementation of forest cover type classification/detection using linear support vector machine implemented with gradient descent from scratch.
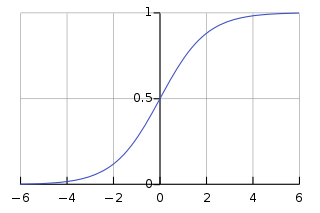
The sigmoid function used for logistic regression has the following curve:
The classification of the hypothesis is considered 1 if sigmoid(z)>=0.5 and 0 if it is <0.5
The cost for such classification without margins is hence:
In this case, we want z (= Theta transpose * X) > 0 for y = 1 and z < 0 for y = 0
Changing the cost functions
Now, if instead of using the logarithmic terms to increase cost for incorrect predictions, we use the following cost0 and cost1 functions, our final cost function looks like:
It can be inferred that the cost is zero when z>=1 for y=1 and increases linearly for z<1. Similarly, the cost is zero when z<=-1 for y=0 and increases linearly for z>-1.
If this new cost function is minimized, it ensures that z > 1 for y = 1 and z < -1 for y = 0, as opposed to the previous case. Hence, it adds a margin of 1 to our predictions, resulting in a better decision boundary/hyperplane.
Maximising margins is the main intuition behind the functioning of support vector machines.
- Model used: Linear SVM using Gradient Descent
- Learning rate: 0.01
- No. of iterations: 500
- No. of features: 26
- No. of classes/labels: 4
- Training data size: 417
- Test data size: 105
- No. of validation tests performed: 5
- Accuracy: 88.6%
Citation for Dataset: Johnson, B., Tateishi, R., Xie, Z., 2012. Using geographically-weighted variables for image classification. Remote Sensing Letters, 3 (6), 491-499.