Doddle exposes four entry points via the command line: run, solve, hide, benchmark
- Run the solver to see how the game is optimally played
- Solve a game in realtime using Doddle's solver
- Play a variation of the game where the solver attempts to hide the answer from you for as long as possible (inspired by Absurdle)
- Benchmark Doddle against the entire dictionary to see how well it performs
The commands can be run with additional parameters:
- Play using words of length 4-9 (inclusive) by adding the optional
--sizeparameter (default is 5). - Choose your solver using the
--solver=ENTROPYor--solver=MINIMAXparameter (default is minimax) - Run deep searches using the
--depthparameter (default is 1) - Solve multiple games of Wordle at the same time. This mode is inspired by popular spin-offs such as Dordle, Quordle and Octordle. Playing multiple games with Doddle is easy: just add more answers to the run command
doddle run --answer=ULTRA,QUICK,SOLVEand Doddle will solve them all at the same time.
Doddle exposes a tonne of features, packed behind a simple API. Wanna play two six-letter word games simultaneously with your choice of an opening guess? Three lines ✨.
from doddle import Doddle
doddle = Doddle(size=6)
scoreboard = doddle(answer=["THOUGH", "FUSION"], guess="PRAYER")Want custom emojis to show how the solver performed?
emojis = scoreboard.emoji()
print(emoji)Doddle 5/7
4️⃣5️⃣
⬜⬜⬜⬜⬜⬜ ⬜⬜⬜⬜⬜⬜
⬜⬜⬜🟨⬜⬜ ⬜🟨🟩⬜⬜⬜
⬜🟨🟨🟨⬜⬜ ⬜🟩⬜🟨⬜⬜
🟩🟩🟩🟩🟩🟩 ⬜⬜🟨🟨⬜⬜
⬛⬛⬛⬛⬛⬛ 🟩🟩🟩🟩🟩🟩
Doddle is not a black box. Create beautiful visualisations with just two lines of code that render the entire decision tree of games. Follow the flow diagram to see how Doddle plays a game. You can render the tree for any choice of opening guess, combination of guesses, depth or solver type.
benchmark = doddle.benchmark(guess="CRATE")
benchmark.digraph()Note that the full tree has been truncated here. Click here to download the full PDF.
Doddle's solver can also be used to generate the optimal decison tree via a recursive search. Alex Selby was the first to prove that SALET yields the optimal decision tree with a total of 7,920 guesses to solve the 2,315 problems from the original Wordle dataset. To generate such a tree using Doddle:
benchmark = doddle.tree_search('SALET')
benchmark
1 | (0)
2 | *** (78)
3 | ************************************************** (1,225)
4 | **************************************** (971)
5 | ** (41)
Guess: SALET
Games: 2,315
Guesses: 7,920
Mean: 3.421
Std: 0.589
Install Doddle with
$ pip install doddle
$ pip install doddle[decision] <--- use this if you want awesome decision trees
Doddle strives to keep dependencies to a minimum. For that reason, the decision tree functionality is included as an optional install and adds an additional dependency on graphviz. Please note that the GraphViz python package assumes you have the (open-source) GraphViz executable correctly installed on your machine. Please see the graphviz documentation for more details.
Doddle includes three entry points as part of the installation process.
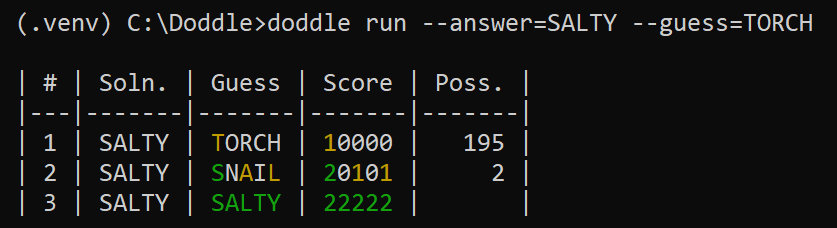
doddle run --answer=SALTY
doddle run --answer=SPEED --guess=SOLVE
doddle run --answer=FABULOUS --guess=SOLUTION,STRENGTH --solver=ENTROPY
doddle run --answer=DEEP --guess=MIND --solver=ENTROPY --depth=2
doddle run --answer=BRAVE,SHAME,TOWER,STEEPRun a simulation with an answer of your choosing to see how Doddle solves the problem. You can optionally provide your own starting guess to see how the game plays out. With every guess, Doddle acquires more information and prunes the list of possible solutions. The output (far right column) shows you how many possible solutions still exist at each step of the solve.
Doddle provides multiple ways to solve the game. You can choose between a minimax solver (the default), or an entropy reduction approach. An entropy based approach optimises for best average play; a minimax approach tries to avoid worst-case scenarios and never goes above 5 moves.
Doddle supports deep searches for all of its solvers 🧠🧠🧠. These are slower, more exhaustive searches for those that want to go deeper. By default, Doddle plays the move that will yield the 'best' outcome on its next turn. In the case of minimax, that means playing the move that will result in the fewest number of possible words to search in the worst-case scenario (it chooses a word that minimises the outcome that provides maximum uncertainty). In the case of --solver=ENTROPY, it plays the move that results in the greatest expected reduction in Shannon entropy. With deep searches, it thinks n steps ahead. So for --depth=2, the minimax solver plays the word that minimses the number of possible solutions in the worst case scenario on the turn after next taking into consideration all sensible first moves. The performance is still decent - a few seconds per game - but it is noticably slower as the search space explodes exponentially with depth.
doddle solve
doddle solve --size=7
doddle solve --guess=RAISE
doddle solve --guess=MIND --solver=ENTROPY
doddle solve --guess=MIND --solver=MINIMAX --depth=2Work smarter not harder. Use Doddle's solver to solve Wordle as fast as possible. If you're playing Wordle and need some... ahem... divine inspiration, fire up Doddle's solver. Doddle will give you the optimal word to use. Type the response back into Wordle to generate the next guess. Doddle represents answers as ternary numbers! Doddle uses 2 for exact matches, 1 for partial matches and 0 for unmatched letters (e.g. 10202).
>>> doddle solve --guess=TORCH
Enter score for TORCH:
>>> 10000
The best guess is SNAIL
Enter score for SNAIL:
>>> 20101
The best guess is SALTY
Enter score for SALTY:
>>> 22222
Great success! ✨ 🔮 ✨
Half way through a game and just want to know the next best move? Doddle's got you covered. With solve, you're not forced to play the move Doddle suggests. Doddle accepts two syntaxes when entering a score: 1) just a score (as above e.g. 20101); or 2) a WORD=SCORE pair (SNAKE=20100). If you're half way through and need the best move, fill in what you've done so far using the second input method and let Doddle take over from there.
The best guess is SNAIL
Enter score for SNAIL:
>>> SNAKE=20100
The best guess is SALTY
...
doddle hide --guess=SALTYHide is a spin on the conventional Wordle game. Here, Doddle uses its solver to hide the final answer for as long as possible. Doddle doesn't choose an answer before the game starts - instead it always presents you with the score that results in maximum ambiguity. You'll get there in the end, but the game might take a while. 😈
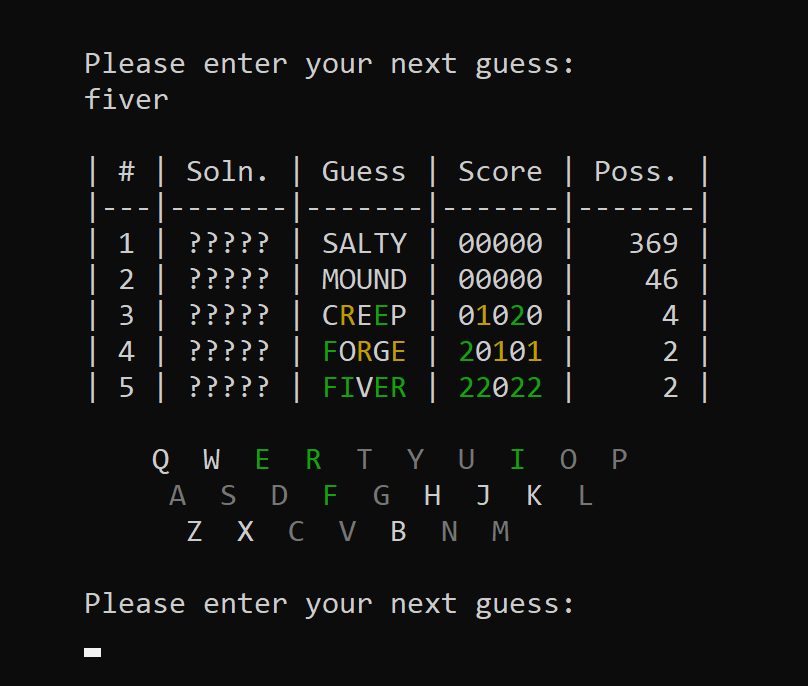
Similar to the original Wordle game, a keyboard is rendered to display what characters have been guessed so far.
doddle benchmark
doddle benchmark --guess=CRATE
doddle benchmark --guess=CRATE --solver=ENTROPY
doddle benchmark --guess=SOLUTION,STRENGTH --solver=ENTROPY
doddle benchmark --guess=MIND --solver=MINIMAX --depth=2
doddle benchmark --simul=4Doddle comes with inbuilt benchmarking capabilities. This allows you to run a configuration of Doddle (e.g. starting guess, solver type, depth etc.) against all words in the dictionary. To benchmark an octordle stlye game (eight simultaneous games), simply add --simul=8.
Doddle is built with performance in mind: a simple 5-letter game under minimax will complete in about 27 seconds on my machine (specs + timings may vary). See how your favourite starting word performs against every word in the dictionary:
>>> doddle benchmark --guess=CRATE --solver=ENTROPY
1 | (1)
2 | *** (83)
3 | ************************************************** (1,204)
4 | **************************************** (968)
5 | ** (58)
Guess: CRATE
Games: 2,314
Guesses: 7,941
Mean: 3.432
Std: 0.608
In addition to running Doddle via the command line, Doddle exposes an intuitive API to be used in code. Simply create a Doddle object to get started.
from doddle import Doddle
doddle = Doddle()
scoreboard = doddle(answer="FLAME")
scoreboardIPython compatible tools such as Jupyter Lab inherently understand Doddle objects and will render them in rich HTML. Simply returning the scoreboard above will render the below:
| Soln | Guess | Score | Poss | |
|---|---|---|---|---|
| 1 | FLAME | RAISE | ⬜🟨⬜⬜🟩 | 41 |
| 2 | FLAME | BLOCK | ⬜🟩⬜⬜⬜ | 7 |
| 3 | FLAME | ADAPT | ⬜⬜🟩⬜⬜ | 2 |
| 4 | FLAME | FLAME | 🟩🟩🟩🟩🟩 |
If you plan to play multiple games using Doddle, it is recommended that you create the Doddle object without lazy evaluation of its internal dictionary.
from doddle import Doddle
doddle = Doddle(lazy_eval=False)This will take a few seconds to initialise, but subsequent solves will be materially faster. To play a 'quordle' style game, with two guesses of your choice, simply call:
scoreboard = doddle(answer=["FLAME","SNAKE","BLAST","CRAVE"], guess=["SHALE","IRATE"])
emojis = scoreboard.emoji()
print(emojis)Doddle 7/9
6️⃣5️⃣
3️⃣7️⃣
⬜⬜🟩🟨🟩 🟩⬜🟩⬜🟩
⬜⬜🟩⬜🟩 ⬜⬜🟩⬜🟩
⬜🟩🟩⬜⬜ ⬜⬜🟩🟨⬜
⬜⬜⬜⬜🟩 ⬜⬜⬜⬜🟩
⬜⬜🟩⬜🟩 🟩🟩🟩🟩🟩
🟩🟩🟩🟩🟩 ⬛⬛⬛⬛⬛
🟨⬜🟩🟨⬜ ⬜⬜🟩⬜🟩
⬜⬜🟩🟨⬜ ⬜🟩🟩⬜🟩
🟩🟩🟩🟩🟩 ⬜⬜🟩⬜⬜
⬛⬛⬛⬛⬛ ⬜⬜⬜⬜🟩
⬛⬛⬛⬛⬛ ⬜⬜🟩⬜🟩
⬛⬛⬛⬛⬛ ⬜⬜🟩⬜🟩
⬛⬛⬛⬛⬛ 🟩🟩🟩🟩🟩
For a simultaneous game such as the one above, the scoreboard object will display the rows associated with each guess in blocks. Try it in Jupyter lab to see the output!
| Soln | Guess | Score | Poss | |
|---|---|---|---|---|
| 1 | FLAME | SHALE | ⬜⬜🟩🟨🟩 | 15 |
| 1 | SNAKE | SHALE | 🟩⬜🟩⬜🟩 | 13 |
| 1 | BLAST | SHALE | 🟨⬜🟩🟨⬜ | 5 |
| 1 | CRAVE | SHALE | ⬜⬜🟩⬜🟩 | 34 |
| 2 | FLAME | IRATE | ⬜⬜🟩⬜🟩 | 10 |
| 2 | SNAKE | IRATE | ⬜⬜🟩⬜🟩 | 4 |
| 2 | BLAST | IRATE | ⬜⬜🟩🟨⬜ | 1 |
| 2 | CRAVE | IRATE | ⬜🟩🟩⬜🟩 | 14 |
| 3 | FLAME | BLAST | ⬜🟩🟩⬜⬜ | 6 |
| 3 | SNAKE | BLAST | ⬜⬜🟩🟨⬜ | 4 |
| 3 | BLAST | BLAST | 🟩🟩🟩🟩🟩 | |
| 3 | CRAVE | BLAST | ⬜⬜🟩⬜⬜ | 11 |
| 4 | FLAME | PUDGE | ⬜⬜⬜⬜🟩 | 2 |
| 4 | SNAKE | PUDGE | ⬜⬜⬜⬜🟩 | 1 |
| 4 | CRAVE | PUDGE | ⬜⬜⬜⬜🟩 | 4 |
| 5 | FLAME | SNAKE | ⬜⬜🟩⬜🟩 | 1 |
| 5 | SNAKE | SNAKE | 🟩🟩🟩🟩🟩 | |
| 5 | CRAVE | SNAKE | ⬜⬜🟩⬜🟩 | 3 |
| 6 | FLAME | FLAME | 🟩🟩🟩🟩🟩 | |
| 6 | CRAVE | FLAME | ⬜⬜🟩⬜🟩 | 2 |
| 7 | CRAVE | CRAVE | 🟩🟩🟩🟩🟩 | |
Additionally, it is easy to access the scoreboard for any individual game. Just use the many() method to decompose a simultaneous scoreboard into a list of available boards.
scoreboards = scoreboard.many()
scoreboards[2]All the benchmarking functionality is exposed via the libary.
doddle = Doddle(solver_type="entropy")
benchmark = doddle.benchmark("CRATE")
benchmarkDoddle also integrates with Wordle Bot so results can be written to the Wordle Bot format for direct upload. Wordle Bot works with a comma separated text file of solutions. To output in the required format:
benchmark.to_csv(filepath)
More importantly, Doddle can create a benchmark from any Wordle Bot text file! Call Benchmark.read_csv(filepath) to load it in and start building decision trees from your own solves. Finally, you can generate an optimal decision tree via a recusive search. To do so:
benchmark = doddle.tree_search(starting_word)
Doddle offers two choices of algorithms for solving Wordle: Minimax and Entropy.
By default, Doddle uses a minimax algorithm to solve the game. The easiest way to explain the algorithm is through example.
Suppose you are half way through a game and have narrowed the solution down to one of four possibilties: SKILL, SPILL, SWILL, STILL.
Clearly, if we work our way through these words sequentially, the worst case scenario will be a further four guesses. To make things precise, let's create a histogram of all the scores that Wordle could return for each guess. We will consider the case where we naïvely choose the word SKILL.
| Guess | Score | Partition Size | Possible Words |
|---|---|---|---|
SKILL |
🟩🟨🟩🟩🟩 | 3 | { SPILL, SWILL, STILL } |
SKILL |
🟩🟩🟩🟩🟩 | 1 | { SKILL } |
The histogram is a great way to see how any guess partitions the remaining words. In the case above, there are two partitions with the worst case scenario being three (because three is the size of the largest partition).
Minimax works by considering all possible words in the dictionary and choosing the word that minimises the size of its largest partition. So, in searching through all possible words, minimax would stumble upon a word like 💥 KAPOW 💥.
| Guess | Score | Partition Size | Possible Words |
|---|---|---|---|
KAPOW |
⬜⬜⬜⬜⬜ | 1 | { STILL } |
KAPOW |
🟨⬜⬜⬜⬜ | 1 | { SKILL } |
KAPOW |
⬜⬜🟨⬜⬜ | 1 | { SPILL } |
KAPOW |
⬜⬜⬜⬜🟨 | 1 | { SWILL } |
In this case, each word is partitioned perfectly into its own bucket of length one and the game can be immediately solved on the next move. It's simple enough to compute this histogram for every possible word and the approach generalises all the way through the game.
As an alternative to minimax, it is possible to play the game using an entropy based approach. Here, the solver always chooses the word that, on average, lowers the Shannon entropy of the game. To see how this works, let's assume we have reduced the game down to 20 possible words and decide to play the (excellent) move THURL. We shall construct a histogram as before - they're very useful.
| Guess | Score | Partition Size | Probability | Possible Words |
|---|---|---|---|---|
THURL |
⬜⬜⬜⬜⬜ | 3 | 0.15 | { SNAKE, SPACE, SPADE } |
THURL |
⬜⬜⬜⬜🟨 | 1 | 0.05 | { SCALE } |
THURL |
⬜⬜⬜🟩⬜ | 3 | 0.15 | { SCARE, SNARE, SPARE } |
THURL |
⬜🟩⬜⬜⬜ | 5 | 0.25 | { SHADE, SHAKE, SHAME, SHAPE, SHAVE } |
THURL |
⬜🟩⬜⬜🟨 | 1 | 0.05 | { SHALE } |
THURL |
⬜🟩⬜🟩⬜ | 2 | 0.10 | { SHARE, SHARK } |
THURL |
🟨⬜⬜⬜⬜ | 3 | 0.15 | { SKATE, STAGE, STAVE } |
THURL |
🟨⬜⬜⬜🟨 | 2 | 0.10 | { SLATE, STALE } |
Under minimax, we would simply look at the largest bucket and assign a score of 5 to the word THURL. However, with an entropy based approach, we take into consideration how much each guess cuts down the entire problem on average. To do that, we need to look at all possible outcomes in the histogram and calculate the expected value of the number of bits of entropy that each guess provides.
The probability of any outcome is calculated simply as the Partition Size / Total Number of Words. The number of bits associated with any outcome is calculates as -log(probability, base=2) and, hence, the expected number of bits is simply the sum of the bits multiplied by their respective probabilities.
In the example above, the expected number of Shannon bits is 2.83 which tells us that the guess THURL roughly cuts the problem size in half 2.83 times. To be explicit, cutting the problem in half once would leave 10 words left to search on average. Cutting the problem in half twice would leave 5. And cutting the problem in half 2.83 times would leave 2.82 words on average which looks eminently sensible when we look at the partition sizes remaining.
The guess with the highest information content, as measured in Shannon bits, is picked. In this case, THURL is pretty optimal.
Work through the tutorials here to see Doddle in action!
- Learn to use Doddle via the API
- Run benchmarks and generate trees
- Calculate the optimal tree for a given starting word using a recursive search
Happy Doddling!