Differatinal Evolution

Single header c++ implementation of a Differential Evolution algorithm for general purpose optimization.

How to install

It is as simple as it gets to use the Differential Evolution for your optimizations. Just add the de/DifferentialEvolution.h header file to your project. It depends only on the standard library and c++11 standard.

Simple usage example

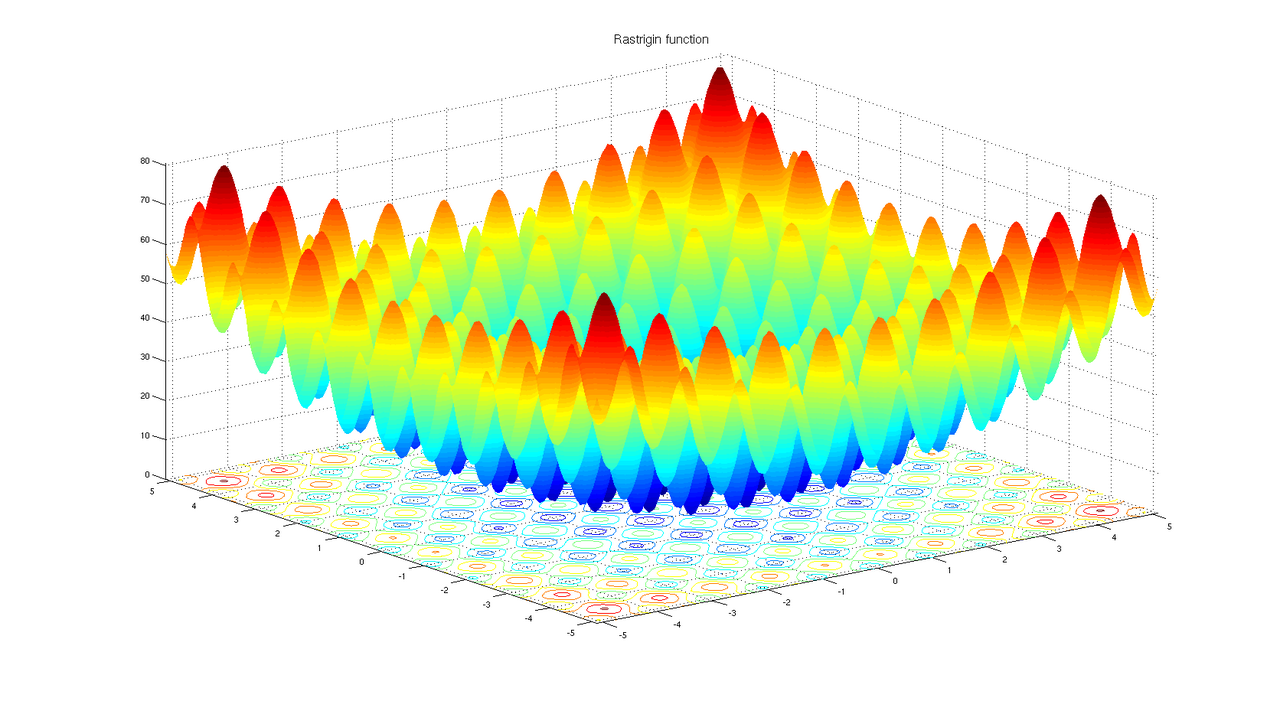
We will use the Differential Evolution to find the global minimum of Rastring test function. This test function can be generalized to N-dimensional optimization problem and below is a plot of the function for the 2D problem. One can see that the Rastring function has a lot of local minimums which makes it fairly hard optimization problem, especially in higher dimensional case.

We will solve 5D Rastring function optimization problem using Differential Evolution with population size of 50 and 1000 iterations. This can be done in just a few lines of code. The Rastring function is provided in the de/TestFunctions.h

#include "de/DifferentialEvolution.h"
#include "de/TestFunctions.h"


int main()
{
    // Creat Rastring's function in 5 dimensions
    de::Rastrigin cost(5);

    // Create Differential Evolution optimizer with population size of 50
    de::DifferentialEvolution de(cost, 50);

    // Optimize for 1000 iterations with verbose output.
    de.Optimize(1000, true);

    return 0;
}

During the optimizations the progress will be outputted as below.

Current minimal cost: 0.03560		Best agent: -0.00591 -0.00004 -0.00192 0.00985 0.00662 
Current minimal cost: 0.01855		Best agent: 0.00622 -0.00104 0.00385 0.00584 -0.00219 

Optimizing your own functions

To optimize your own function just implement the simple interface IOptimizable like it is done below for a trivial quadratic function. One should note the Differential Evolution is general purpose black box optimization problem which means that you may use any kind of code in the function definition, there are no assumptions to be fulfilled.

#include "de/DifferentialEvolution.h"

#include <ctime>

class SimpleQuadriatic : public de::IOptimizable
{
public:
    double EvaluteCost(std::vector<double> inputs) const override
    {
        assert(inputs.size() == 2);

        double x = inputs[0];
        double y = inputs[1];

        return x * x + 2 * x * y + 3 * y * y;
    }

    unsigned int NumberOfParameters() const override
    {
        return 2;
    }

    std::vector<Constraints> GetConstraints() const override
    {
        std::vector<Constraints> constr(NumberOfParameters());
        for (auto& c : constr)
        {
            c = Constraints(-100.0, 100.0, true);
        }
        return constr;
    }
};

int main()
{
    SimpleQuadriatic cost;

    de::DifferentialEvolution de(cost, 100, std::time(nullptr));

    de.Optimize(1000, true);

    return 0;
}

Author: Milos Stojanovic Stojke