-
Notifications
You must be signed in to change notification settings - Fork 11
Hamiltonians
File Hamiltonians.py includes the definition of all the functions which generate the terms of the Hamiltonian of the nuclear spin.
In quantum mechanics, the Hamiltonian of a physical system is the operator associated to its energy. It is a privileged observable, since it plays a central role in the problem of the dynamics of the system.
In the present simulation program, we study the dynamics of a nuclear spin under the effect of three main interactions:
- Zeeman interaction with an external stationary magnetic field;
- Quadrupolar interaction with the electric field gradient generated by surrounding electrons;
- Electromagnetic coupling with an oscillating magnetic field applied in the time-interval [0, t].
Each one of these contributions is represented by a distinct function, which takes as arguments the dynamical and fixed parameters which appear in the expression of the Hamiltonian (including time, in the third case) and returns an Observable object which embodies the corresponding Hamiltonian. In the general case, the third contribution is made up of the superposition of many independent single-mode electromagnetic waves. For this reason, two functions have been defined: H_Single_Mode_Pulse and H_Multiple_Mode_Pulse.
-
h_zeeman(spin, theta_z, phi_z, B_0)Computes the term of the Hamiltonian associated with the Zeeman interaction between the nuclear spin and the external static field. The mathematical formula for this quantity is the following:

Parameters
-
spin:Nuclear_SpinSpin under study;
-
theta_z:floatPolar angle of the magnetic field in the laboratory coordinate system (expressed in radians);
-
phi_z:floatAzimuthal angle of the magnetic field in the laboratory coordinate system (expressed in radians);
-
B_0: non-negativefloatMagnitude of the external magnetic field (expressed in tesla).
Returns
An
Observableobject which represents the Zeeman Hamiltonian in the laboratory reference frame (expressed in MHz).Raises
ValueError, when the passedB_0is a negative number. -
-
h_quadrupole(spin, e2qQ, eta, alpha_q, beta_q, gamma_q)Computes the term of the Hamiltonian associated with the quadrupolar interaction. The mathematical formula for this quantity is the following:

where V0, V+/-1, V+/-2 are the electric field gradient (EFG) tensor's spherical components (divided by the parameter eq), represented by the functions
v0_EFG,v1_EFG,v2_EFGdescribed below.Parameters
-
spin:Nuclear_SpinSpin under study;
-
e2qQ:floatProduct of the quadrupole moment constant, eQ, and the eigenvalue of the EFG tensor which is greatest in absolute value, eq.
e2qQis measured in MHz; -
eta:floatin the interval [0, 1]
Asymmetry parameter of the EFG;
-
alpha_q,beta_q,gamma_q:float
Euler angles for the conversion from the lab coordinate system (LAB) to the system of the principal axes of the EFG tensor (PAS) (expressed in radians).
Returns
If the quantum number of the spin is 1/2, the whole calculation is skipped and a null
Observableobject is returned.Otherwise, the function returns the
Observableobject which represents the quadrupolar Hamiltonian in the laboratory reference frame (expressed in MHz). -
-
v0_EFG(eta, alpha_q, beta_q, gamma_q)Returns the component V0 of the EFG tensor (divided by eq) as seen in the LAB system. This quantity is expressed in terms of the Euler angles which relate PAS and LAB systems and the parameter
etaas shown in the following formula:
Parameters
-
eta:floatin the interval [0, 1]Asymmetry parameter of the EFG;
-
alpha_q,beta_q,gamma_q:floatEuler angles for the conversion from the lab coordinate system (LAB) to the system of the principal axes of the EFG tensor (PAS) (expressed in radians).
Returns
A
floatrepresenting the component V0 (divided by eq) of the EFG tensor evaluated in the LAB system.Raises
ValueError, when the passedetais not in the interval [0, 1]. -
-
v1_EFG(sign, eta, alpha_q, beta_q, gamma_q)Returns the components V+/-1 of the EFG tensor (divided by eq) as seen in the LAB system. These quantities are expressed in terms of the Euler angles which relate PAS and LAB systems and the parameter
etaas shown in the following formula: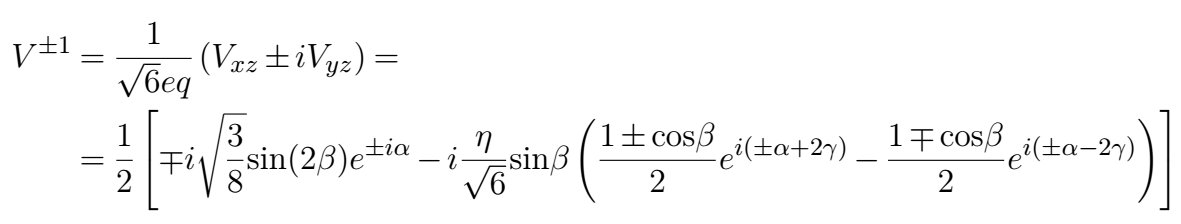
Parameters
-
sign:floatSpecifies wether the V+1 or the V-1 component is to be computed;
-
eta:floatin the interval [0, 1]Asymmetry parameter of the EFG;
-
alpha_q,beta_q,gamma_q:floatEuler angles for the conversion from the lab coordinate system (LAB) to the system of the principal axes of the EFG tensor (PAS) (expressed in radians).
Returns
A complex number representing the component:
-
V+1, if
signis positive; -
V-1, if
signis negative.
of the EFG tensor (divided by eq).
Raises
ValueError, when the passedetais not in the interval [0, 1]. -
-
v2_EFG(sign, eta, alpha_q, beta_q, gamma_q)Returns the components V+/-2 of the EFG tensor (divided by eq) as seen in the LAB system. These quantities are expressed in terms of the Euler angles which relate PAS and LAB systems and the parameter
etaas shown in the following formula:
Parameters
-
sign:floatSpecifies wether the V+2 or the V-2 component is to be returned;
-
eta:floatin the interval [0, 1]Asymmetry parameter of the EFG tensor;
-
alpha_q,beta_q,gamma_q:floatEuler angles for the conversion from the lab coordinate system (LAB) to the system of the principal axes of the EFG tensor (PAS) (expressed in radians).
Returns
A
floatrepresenting the component:-
V+2, if
signis positive; -
V-2, if
signis negative.
of the EFG tensor (divided by eq).
Raises
ValueError, when the passedetais not in the interval [0, 1]. -
-
h_single_mode_pulse(spin, frequency, phase, B_1, theta_1, phi_1, t)Computes the term of the Hamiltonian describing the interaction with a monochromatic and linearly polarized electromagnetic pulse. The mathematical formula for this quantity is the following:

where all quantities labelled with the subscript 1 belong to the oscillating magnetic component B1 of the electromagnetic wave.
Parameters
-
spin:Nuclear_SpinSpin under study.
-
frequency: non-negativefloatFrequency of the monochromatic wave (expressed in MHz).
-
phase:floatInital phase of the wave (at t=0) (expressed in radians).
-
B_1: non-negativefloatMaximum amplitude of the oscillating magnetic field (expressed in tesla).
-
theta_1,phi_1:floatPolar and azimuthal angles of the direction of polarization of the magnetic wave in the LAB frame (expressed in radians);
-
t:floatTime of evaluation of the Hamiltonian (expressed in microseconds).
Returns
An
Observableobject which represents the Hamiltonian of the coupling with the electromagnetic pulse evaluated at timet(expressed in MHz).Raises
ValueError, in two distinct cases:- When the passed
frequencyparameter is a negative quantity; - When the passed
B_1parameter is a negative quantity.
-
-
h_multiple_mode_pulse(spin, mode, t)Computes the term of the Hamiltonian describing the interaction with a superposition of single-mode electromagnetic pulses. If the passed argument
spinis aNuclear_Spinobject, the returned Hamiltonian will describe the interaction between the pulse of radiation and the single spin; if it is aMany_Spinsobject, it will represent the interaction with the whole system of many spins. The mathematical formula of this term of the Hamiltonian for a single spin is the following:
where all quantities labelled with the subscript i belong to the single mode of the magnetic field Bi.
Parameters
-
spin:Nuclear_SpinorMany_SpinsSpin or spin system under study;
-
mode:pandas.DataFrameTable of the parameters of each electromagnetic mode in the superposition. It is organised according to the following template:
index 'frequency''amplitude''phase''theta_p''phi_p'(MHz) (T) (rad) (rad) (rad) 0 omega_0 B_0 phase_0 theta_0 phi_0 1 omega_1 B_1 phase_1 theta_1 phi_1 ... ... ... ... ... ... N omega_N B_N phase_N theta_N phi_N where the meaning of each column is analogous to the corresponding parameters in
h_single_mode_pulse. -
t:floatTime of evaluation of the Hamiltonian (expressed in microseconds).
Returns
An
Observableobject which represents the Hamiltonian of the coupling with the superposition of the given modes evaluated at timet(expressed in MHz). -
-
h_changed_picture(spin, mode, h_unperturbed, h_change_of_picture, t)Returns the global Hamiltonian of the system, made up of the time-dependent term
h_multiple_mode_pulse(spin, mode, t)and the stationary termh_unperturbed, cast in the picture generated byh_change_of_picture.Parameters
-
spin,mode,t: same meaning as the corresponding arguments ofh_multiple_mode_pulse; -
h_unperturbed:OperatorStationary term of the global Hamiltonian (in MHz);
-
h_change_of_picture:OperatorOperator which generates the new picture (in MHz).
Returns
Observableobject representing the Hamiltonian of the pulse evaluated at timetin the new picture (in MHz). -
-
h_j_coupling(spins, j_matrix)Returns the term of the Hamiltonian describing the J-coupling between the spins of a system of many nuclei, computed through the following formula

Parameters
-
spins:Many_SpinsSpins' system under study;
-
j_matrix:np.ndarrayArray storing the coefficients Jmn which enter the formula above.
Remark:
j_matrixdoesn't have to be symmetric, since the function reads only those elements located in the upper half of the array with respect to its diagonal. This means that the elementsj_matrix[m, n]which matter are those for whichm<n.
Returns
Observableobject acting on the full Hilbert space of the spins' system representing the Hamiltonian of the J-coupling between the spins. -