This Repository Contains code related to Simulation Fluid Following Navier-Stokes Spectral Method under the assumption of it being incompressible viscous fluid
Navier-Stokes equations (incompressible viscous fluid) with a Spectral method
A spectral method represents the numerical solution to a partial differential equation as a sum of global basis functions with coefficients as the unknowns to be solved for. Here we will consider the Fourier basis, which is ideal for representing continuous solutions on a periodic domain. Such a method can then use the Fast Fourier Transform (FFT) algorithm to transform the solution on the physical domain x into Fourier space, where the solution becomes a sum of waves each described by a wavenumber k.
Create Your Own Navier-Stokes Spectral Method Fluid Simulation (With Python)
Author is Philip Mocz. Special Thanks to him
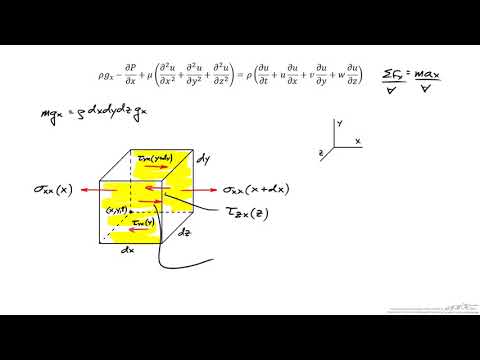
The Navier-Stokes Equation is one of the Millenium Prize Problems
There have been some interesting developments in 2024 regarding the existence and smoothness of solutions to the Navier-Stokes equation. A notable paper by Brian David Vasquez Campos presents a smooth solution to the Navier-Stokes equation. This solution is constructed by studying the iteration of a product defined over a space of functions dominated by Fourier caloric functions that decrease rapidly. Additionally, the paper shows the existence of a curve of entire vector fields of order 2 that extends the solution to the complex domain for positive time (https://arxiv.org/pdf/2405.07929)
This is a significant step forward in understanding the Navier-Stokes equation, which is fundamental in fluid dynamics and has implications for various fields, including weather forecasting, aircraft design, and biomedical engineering.