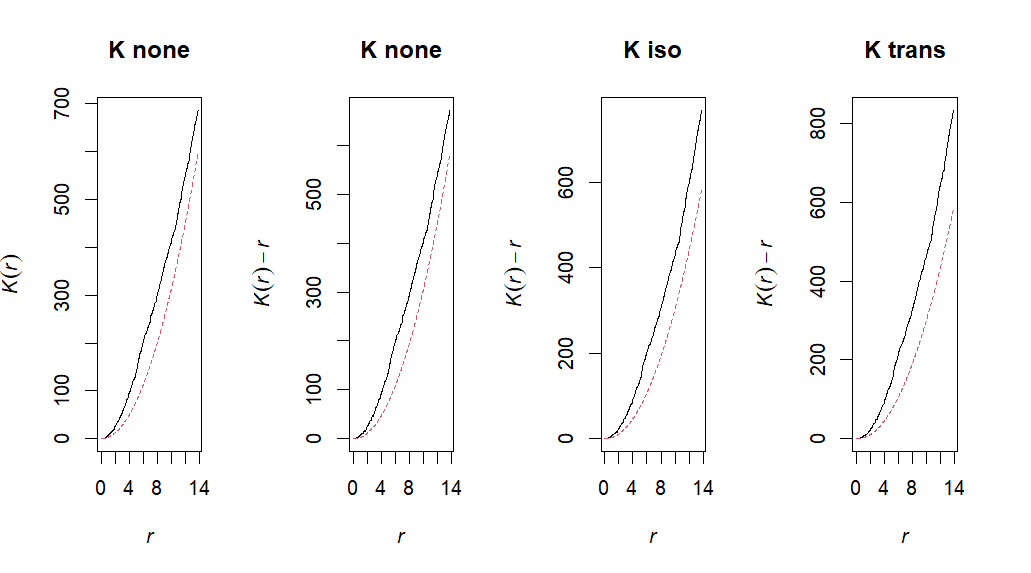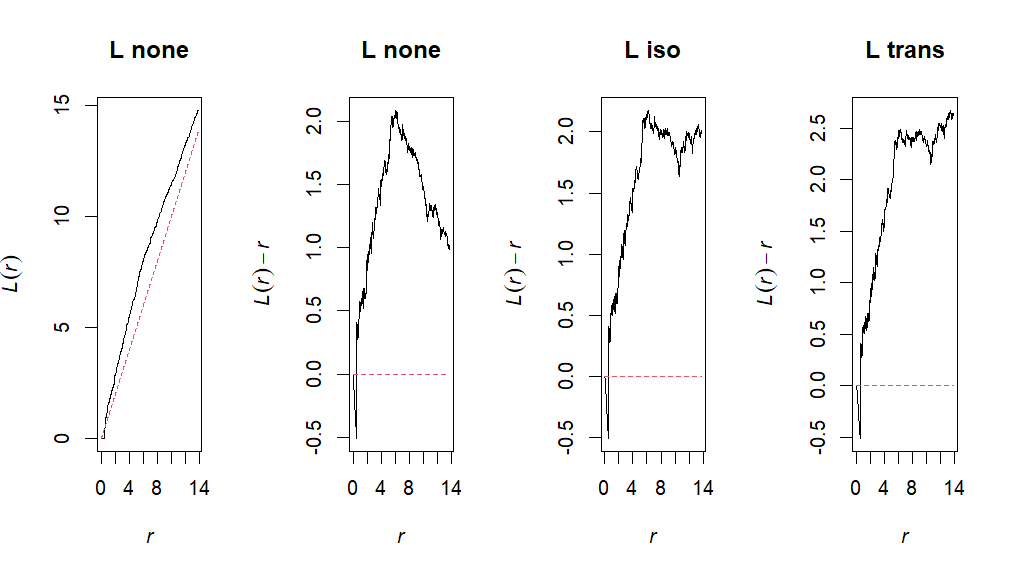Point pattern analysis is a statistical technique used to analyze the patterns formed by points in a space, particularly clustering versus dispersion of observations. We can utilize the spatstat package in order to go through various functions which quantify clustering and dispersion throughout our dataset. This script outlines how you would conduct a spatial point pattern analysis!
require(spatstat)
require(spatstat.data)
require(spdep)
require(sf)
require(here)# Load in Data
pts <- read.csv(here("data", "cactus.csv"))
boundary <- read.csv(here("data", "cactus_boundaries.csv"),header=T)
# Create a spatstat object with our pts data
ppp.window <- owin(xrange=c(boundary$Xmin, boundary$Xmax),
yrange=c(boundary$Ymin, boundary$Ymax))
ppp <- ppp(pts$East, pts$North, window=ppp.window)par(mfrow = c(1,2), oma=c(0,0,0,1))
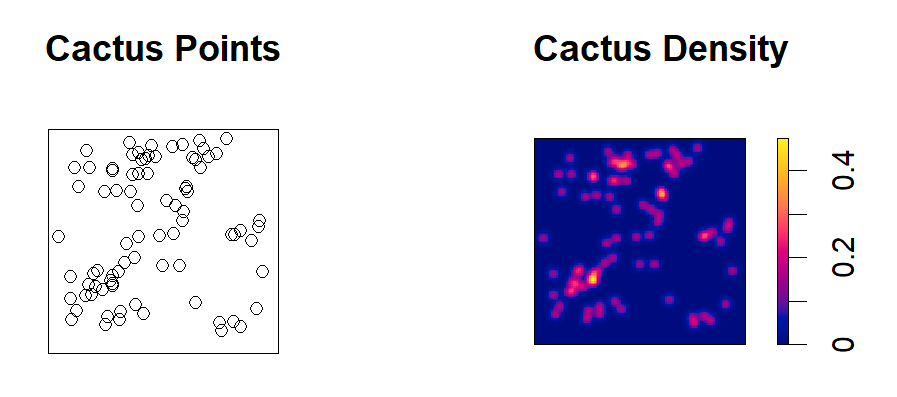
plot(ppp, main = "Points")
plot(density(ppp,1), main = "Density")summary(ppp)# K 1:1 expectation (no correction)
Knone <- Kest(ppp, correction="none")
# K with Isotropic edge correction
Kiso <- Kest(ppp, correction="isotropic")
# K with Translate (toroidal) edge correction
Ktrans <- Kest(ppp, correction="trans")# Plot
ppp_plot("K", Knone, Kiso, Ktrans)# L 1:1 expectation (no correction)
Lnone <- Lest(ppp, correction="none")
# L with Isotropic edge correction
Liso <- Lest(ppp, correction="isotropic")
# L with Translate (toroidal) edge correction
Ltrans <- Lest(ppp, correction="trans")# Plot
ppp_plot("L", Lnone, Liso, Ltrans)# g 1:1 expectation (no correction)
Pnone <- pcf(ppp, correction="none")
# g with Isotropic edge correction
Piso <- pcf(ppp, correction="isotropic")
# g with Translate (toroidal) edge correction
Ptrans <- pcf(ppp, correction="trans")# Plot
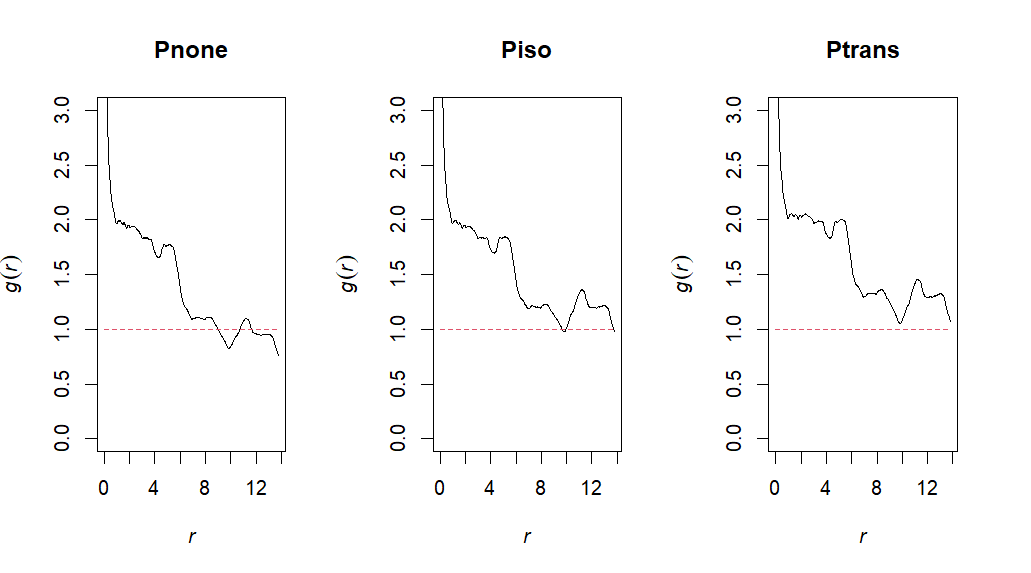
par(mfrow = c(1,3))
plot(Pnone, main = "Pnone",legend=F, ylim=c(0,3))
plot(Piso, main = "Piso", legend=F, ylim=c(0,3))
plot(Ptrans, main = "Ptrans", legend=F, ylim=c(0,3))# G 1:1 expectation (no correction)
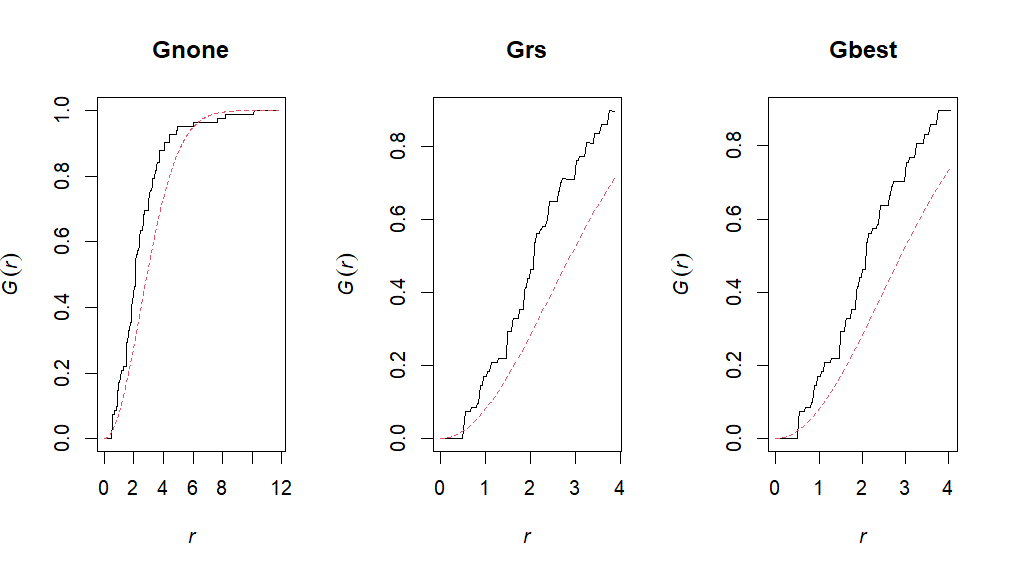
Gnone <- Gest(ppp, correction="none")
# G with Reduced sample or border correction
Grs <- Gest(ppp, correction="rs")
# G with Best (determines best correction for dataset)
Gbest = Gest(ppp, correction="best")# Plot!
par(mfrow = c(1,3))
plot(Gnone, main = "Gnone",legend=F)
plot(Grs, main = "Grs", legend=F)
plot(Gbest, main = "Gbest", legend=F)# F 1:1 expectation (no correction)
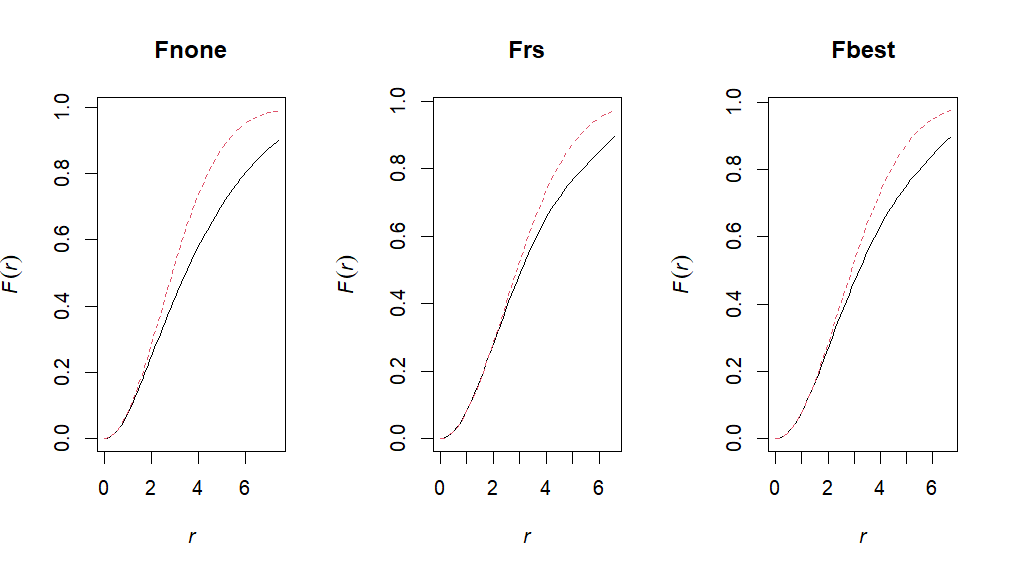
Fnone <- Fest(ppp, correction="none")
# F with Reduced sample or border correction
Frs <- Fest(ppp, correction="rs")
# F with Best (determines best correction for dataset)
Fbest = Fest(ppp, correction="best")# 9.4: Plot!
par(mfrow = c(1,3))
plot(Fnone, main = "Fnone",legend=F)
plot(Frs, main = "Frs", legend=F)
plot(Fbest, main = "Fbest", legend=F)# Create a global & pointwise (non-global) Envelope
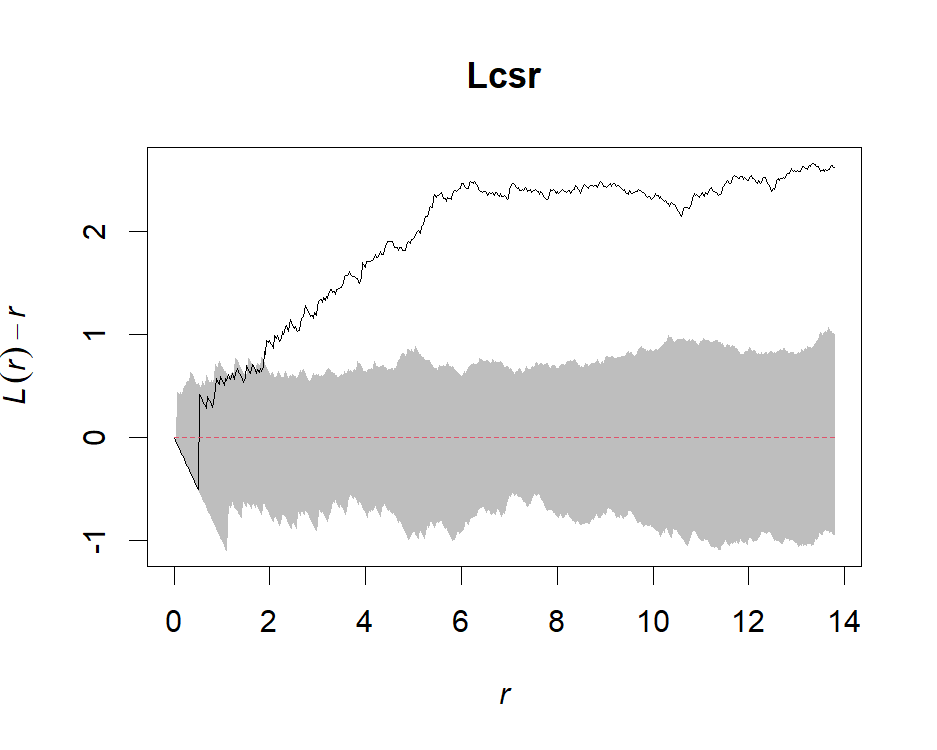
Lcsr <- envelope(ppp, Lest, nsim=99, rank=1, correction="trans", global=F)
Lcsr.g <- envelope(ppp, Lest, nsim=99, rank=1, correction="trans", global=T)# Plot point-wise envelope
plot(Lcsr, . - r~r, shade=c("hi", "lo"), legend=F)
# Plot global envelope
plot(Lcsr.g, . - r~r, shade=c("hi", "lo"), legend=F)# Create a fine envelope
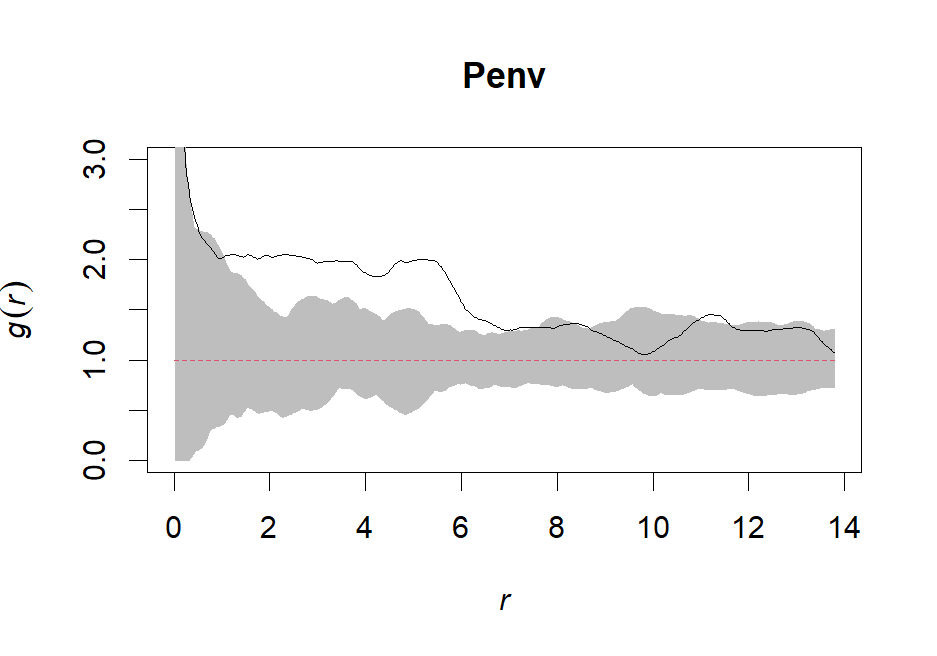
Penv <- envelope(ppp,pcf, nsim=99, rank=1, stoyan=0.15, correction="trans", global=F)#stoyan = bandwidth; set to default
# Create a coarse envelope
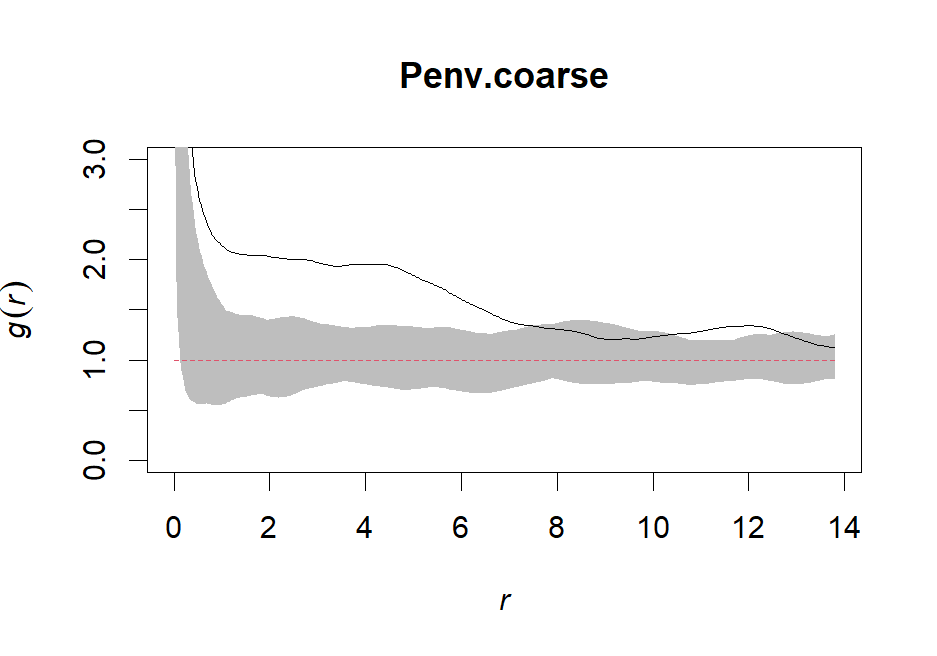
Penv.coarse <- envelope(ppp, pcf, nsim=99, rank=1, stoyan=0.3, correction="trans", global=F)# Plot our fine envelope
plot(Penv, shade=c("hi", "lo"), legend=FALSE, ylim = c(0,3))
# Plot our coarse envelope
plot(Penv.coarse, shade=c("hi", "lo"), legend=F, ylim = c(0,3))# Create a pointwise Gest envelope
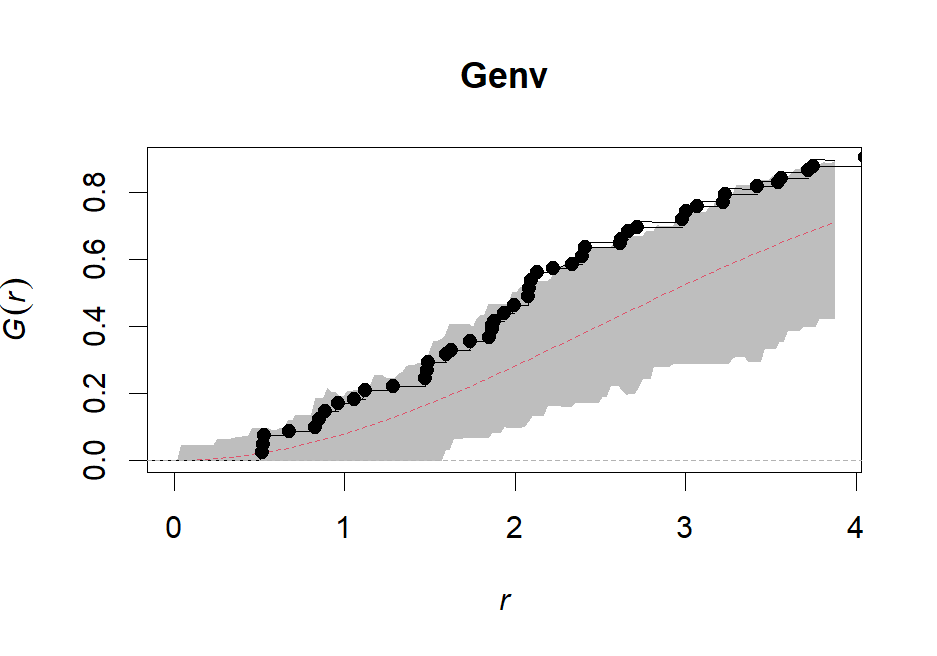
Genv <- envelope(ppp, Gest, nsim=99, rank=1, correction="rs", global=F)
# Create a nearest neighbor distance variable for our plot
nn.dist <- nndist(ppp)
max(nn.dist)# Plot our trans G
plot(Gtrans, legend=F)
# Plot G with our pointwise envelope & nearest neighbor distances
plot(Genv, shade=c("hi", "lo"), legend=F)
plot(ecdf(nn.dist), add=T)# Load in our example dataset
data(spruces)
# Create an envelope for spruces
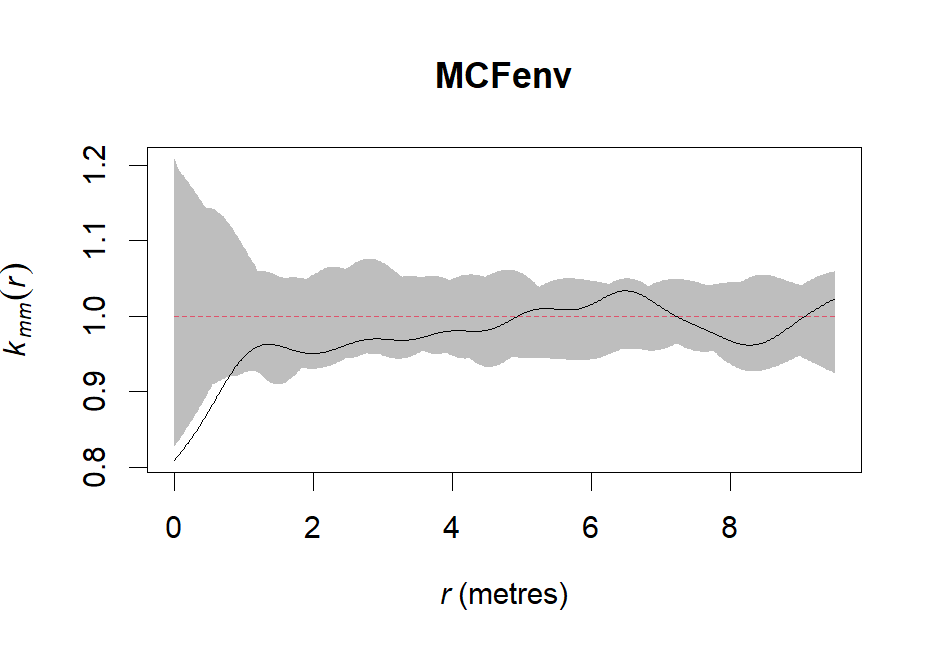
MCFenv <- envelope(spruces, markcorr, nsim=99, correction="iso", global=F)# Plot envelope
plot(MCFenv, shade=c("hi", "lo"), legend=F)