prelecture_02_electric_fields

Electric Fields

Overview

• Coulomb's Law
  • [ {\vec F_{ iq}} = k \frac{ {{Q_i}{q}}}{ {r_{ iq}^2}} {\hat r_{ iq}}]
• Superpossition
  • [ {\vec F = {\sum\limits_i \vec F_{iq}} = kq {\sum\limits_i \frac{ Q_i}{ r_{iq}^2} \hat r_{iq}]
• Point Charge
  • [ E = k \frac{ Q}{ r^2} ]
• Infinite Line of Charge
  • [ E = 2k \frac{\lambda }{ r} ]

Electric Fields

• Electric Field
  • [{\vec E \equiv \frac{ \vec F}{ q} ]
  • [{\vec E_1 \equiv \frac{ \vec F_{12}}{ q_2} = k \frac{ q_1}{ r^2} \hat r]
  • [{\vec E_Q \equiv \frac{ \vec F}{ q} = k \frac{Q}{ r^2} \hat r]

Example: A point Charge

• Electric Field

  • [{\vec E_Q \equiv \frac{ \vec F}{ q} = k \frac{Q}{ r^2} \hat r]

• A single point charge creates a perfectly cylindrically symmetrical field.

Question 1

In the diagrams below, the magnitude and direction of the electric field is represented by the length and direction of the blue arrows. Which of the diagrams best represents the electric field from a negative charge?

• (d)
  • The only difference between the field from the positive charge and the negative charge is that the direction changes. Namely, the field always points away from the positive charge, since the force it would exert on another positive charge would be repulsive, directed away from the initial charge. The field always points towards from the negative charge, since the force it would exert on a positive charge would be attractive, directed towards the initial charge.

The Electric Dipole

• Two opposite charges of equal magnitude.
• Determinign the force at some point [P].
  • Calculate the electric fields separately at point [P] and then take the vector sum.

Question 2

An electric dipole (two opposite charges of equal magnitude) is oriented along the [y] axis as shown. You are not told which charge is positive, but you know the electric field at a point [P] on the [y] axis is as shown by the green arrow.

If the bottom charge is removed, which of the following best describes what happens to the electric field at [P]?

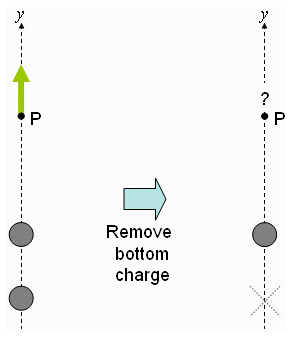
• The magnitude increases and the direction stays the same.
  • Since both charges have the same magnitude, and since point [P] is closer to the top charge than to the bottom charge, the direction of [E] at point [P] tells us that the top charge is positve and the bottom charge and that their field add as shown to give the total field at [P]:
  • Since the contributions to the field at [P] from the positive and negative charges partially cancel when both chargs are present, removing the bottom charge will increase the total field.

Infinite Line of Charge

• [ E_y = 2k \frac{\lambda }{ r} ]

Question 3

A thin rod with length L has a total charge of Q distributed uniformly along it’s length is located on the x-axis with one end at the origin as shown.

Which expression represents the electric field due to this rod at a point on the [x]-axis a distance [a] to the left of the origin?

• [ E_x = - \int\limits_0^L { k \frac{ Q}{ L(a+x)^2}}dx ]
  • [Q] times [\frac{ dx}{ L}] represents the element of charge [dq] contained by a small segment of the line of length [dx], and [(a+x)^2] is the square of the distance from the point of interest to the element of charge at location [x]. The integral therefore sums up the quantity [k \frac{dq}{ r^2}] for the entire line of charge, which is precisely what we need.

Summary

• Descrete Distribution
  • [ \vec E \equiv \frac{ \vec F}{ q} = \frac{ 1}{ q} \sum\limits_i{ \vec F_{iq}} = k \sum\limits_i{ \frac{ Q_i}{ r_{iq}^2} \hat r_{iq}}]
• Continuous Distribution
  • [ \vec E \equiv \frac{ \vec F}{ q} = \frac{ 1}{ q} \int{ d \vec F} = k \int{ \frac{ d Q}{ r^2} \hat r}]