-
Notifications
You must be signed in to change notification settings - Fork 52
prelecture_07_conductors_and_capacitance
- Today will extend our study of electric potential to
- Conductors
- Capacitance
- We will introduce this topic
- Last time we introduced Electric Potential
- [\Delta V_{A \rightarrow B} = -\int\limits_{A}^{B}{ \vec E \cdot d \vec l}]
- All example shown had fixed charge distrobutions, today we will introduce conductors without a fixed charge distrobution. * Conductors where the charges are free to move
- After discussing non-uniform charge distrobution in a conductor, we go on to discuss capacitance
- Specifically we discuss parallel plates
- [C \equiv \frac{ Q}{ \Delta V}]
- Field betwee plates [E = \frac{ Q}{ \varepsilon_0 A}]

- [V_B - V_A = -\int\limits_{A}^B}{ \vec E \cdot d \vec l}]
- [V_B - V_A = 0]
- Since [\vec E = 0] everywhere within the conductor
- This implies that the entire conductor it self is an equipotential

- When the conductor is circularly symmetric, the field lines are perpendicular to the surface

- When we change the shape such that it is no longer circularly symmetric the charge density redistributes such that we have varying points of charge density
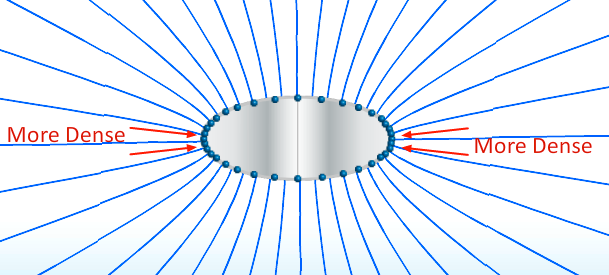
A solid elliptical conductor with a net charge [Q] is surrounded by a hollow spherical conductor with net charge [-Q]. Points [a] and [c] are on the outer surface of the inner conductor, and points [b] and [d] are on the inner surface of the outer conductor as shown.
Compare [V_{ab}], the magnitude of the potential difference between points [a] and [b], to [V_{cd}], the magnitude of the potential difference between points [c] and [d].

- [V_{ab} = V_{cd}]
- Since each conductor is an equipotential, the potential difference between any point on the inner conductor and any point on the outer conductor has to be the same.

-
Consider two conducting spheres which are seprerated by a large distance and have radius' [R_A] and [R_B = 4 R_A]
-
Calculating the potential at the surface of [A]
- [V_A = -\int\limits_{\infty}^{R_A}{ \vec E_A \cdot d \vec l}]
- [V_A = -\int\limits_{\infty}^{R_A}{ k \frac{ Q}{ r^2} d r}]
- [V_A = k \frac{ Q}{ R_A}]
-
Repeat for sphere [B]
- [V_B = k \frac{ Q}{ R_B}]
- [V_B = k \frac{ Q}{ 4 R_A}]
- [V_B = \frac{ 1}{ 4} V_A]

- What if we connect the sphere's via a thin wire?
- The charges will in essence become a single conductor
- Their charges will flow until the come to the same potential.
- [V_A = V_B]
- [k \frac{ Q_A}{ R_A} = k \frac{ Q_B}{ R_B}]
- [k \frac{ Q_A}{ R_A} = k \frac{ Q_B}{ 4 R_A}]
- [\frac{ Q_A}{ R_A} = \frac{ Q_B}{ 4 R_A}]
- [Q_A = \frac{ Q_B}{ 4}]
- [ 4 Q_A = Q_B]
- [ Q_A + Q_B = 2 Q]
- [ Q_A = \frac{ 2}{ 5} Q]
- [ Q_B = \frac{ 8}{ 5} Q]
- Note
- Even though sphere [B] has four times the charge of sphere [A] the charge density on sphere [A] is still larger.
- [4 Q_A = Q_B]
- [4 \sigma_A Area_A = \sigma_B Area_B ]
- [4 \sigma_A 4 \pi R_A^2 = \sigma_B 4 \pi R_B^2 ]
- [4 \sigma_A R_A^2 = \sigma_B R_B^2 ]
- [4 \sigma_A R_A^2 = \sigma_B (4 R_A)^2 ]
- [4 \sigma_A R_A^2 = \sigma_B 4^2 R_A^2 ]
- [4 \sigma_A = \sigma_B 4^2]
- [\sigma_A = \sigma_B 4]
- [\sigma_A = 4 \sigma_B]
- Uncharged spherical conducting shell with a positive charge placed in the cavity.

- The presence of the positive charge will cause the charges in the conducting
shell to move so as to preserve the zero electric field in the center
* QUESTION: This was an uncharged spherical shell, why is it worded this way in the prelecture??
- Consequently both surfaces of the shell receive an induced charge.
- [Q_{inner} = -q]
- [Q_{outer} = q]

- Should the charge at the center of the sphere move to the right
- Inner surface charge distribution changes accordingly.
- Outer surface charge distribution stays the same.
Consider a charged solid conducting sphere of radius [a] inside an uncharged hollow conducting sphere having inner radius [b] and outer radius [c], as shown.
Which of the following graphs best describes the magnitude of the electric field as a function of distance [r] from the center of the sphere?

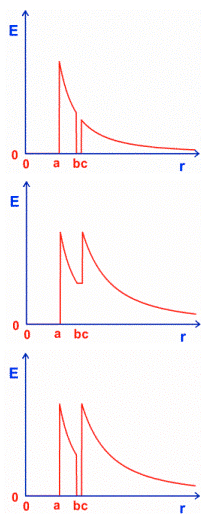
- A
- According to Gauss law the [E]-field will simply diminish as [\frac{ 1}{ r^2}] when is [r > a]. Since the outer conducting shell is uncharged it does not contribute to [E] in any way other than ensuring that [E = 0] inside the shell itself (i.e., for [b < r < c]).
- We just explored what happens when we move a charge around the inside of a conducting spherical shell.

- Now we will explore what happens when you do the same outside the shell.

-
Similarly the charge distribution on the outer shell will act accordingly to the position of the outer charge [q].
-
Now consider if we create a cavity within the solid conductor

- Similarly again, the charge on the inner cavity remains unchanged by presence of the charge outside the conducting shell.
- The inner charge field of the conducting sphere always remains zero and the charges position them selves in such a manor to act accordingly.

- Let
- [\vec E] be the electric field between the plates
- [\Delta V] non-zero potential difference which develops as a result of this field.
- Since
- [E \propto Q]
- Then
- [\Delta V \propto Q]
- So we define the capacitance to be
- [C \equiv \frac{ Q}{ \Delta V}]
- The units of capacitance are Coulomb per Volt which is a Farad
- [ F = \frac{ C}{ V}]

- Let
- [A] be the surface area of the conducting plates
- [d] be the distance between the plates
- [L] be the edge lengths of the plates
- [\vec E] be the electric field created between the plates
- [ d << L]
- Given
- The magnitude of the [E] field created separately
- [E_{Top Plate} = \frac{ 1}{ 2} \frac{ \sigma}{ \varepsilon_0}]
- [E_{Bottom Plate} = \frac{ 1}{ 2} \frac{ \sigma}{ \varepsilon_0}]
- [E_{Top Plate} = \frac{ 1}{ 2} \frac{ Q}{ \varepsilon_0 A}]
- [E_{Bottom Plate} = \frac{ 1}{ 2} \frac{ Q}{ \varepsilon_0 A}]
- The magnitude of the [E] field created separately
- Then
- Since directions of their fields is the same, we determine that
- [E = \frac{ 1}{ 2} \frac{ Q}{ \varepsilon_0 A}]
- Since directions of their fields is the same, we determine that
- Now looking for the potential difference in [C \equiv \frac{ Q}{ \Delta}{ V}]
- [\left|\Delta V\right| = \int\limits_{bottom}^{top}{ \vec E \cdot d \vec l}]
- [\left|\Delta V\right| = \int\limits_{bottom}^{top}{ \frac{ Q}{ \epsilon_0 A} d y}]