prelecture_09_electric_currents

Electric Currents

Overview

• So far: Electrostatics
  • 
  • 
• Electrodynamics
  • [I \equiv \frac{ d q}{ d t}]
• Ohm's Law
  • [J = \sigma E]
• Resistance
  • 

Current: Qualitative Description

• [I = \frac{ d q}{ d t}]
  • SI Units [ A = \frac{ C}{ S}] or Ampere equals coulomb per second

Current: Quantitative Description

• Current Density [J]
  • [J \equiv \frac{ I}{ A}] where [I] is the total current and [A] is the area of a circular section of the cylinder.
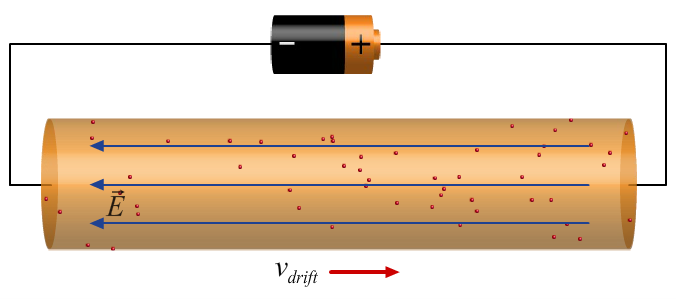
  • [J \equiv \frac{ I}{ A} = ] where [n_e] is the number conduction electrons per unit volume, [e] is the charge on a single electron, [v_{drift}] is the average volocity of the conduction electrons.
    • [n_e = N_A \frac{ \rho_{mass}}{ M}]
  • Ohm's Law
    • [J \propto E]
    • [J = \sigma E], where [\sigma] is the conductivity of the material
    • [v_{drift} = \frac{ \sigma}{ n_e e } E]
      • directed towrd the positive end of the battery

Resistance

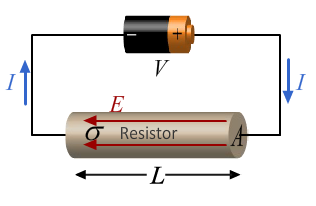
• [J = \sigma \frac{ V}{ L}]
• Since
  • [J \equiv \frac{ I}{ A} = \sigma \frac{ V}{ L}]
  • [R \equiv \frac{ V}{ I}]
• We find
  • [R = \frac{ 1}{ \sigma} \frac{ L}{ A}]
  • [R = \rho \frac{ L}{ A}]

Question 1

Two cylindrical resistors are made from the same material. The shorter one has length [L] and diamater [D]. The longer one has length [16L] and diameter [4D].

How do their resistances compare?

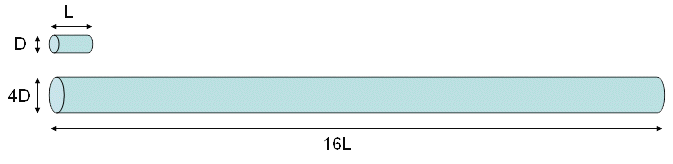
• The resistance of the longer one is the same as the resisitance of the shorter one.
  • The resistance of each is proportional to its length divided by its area. Since the longer one has 16 times the length but also has 16 times the area (i.e. four times the diameter), its overall resistance is the same as the shorter one.

Resistors in Series

• Resistors in series are equivelent to one large resistor where
  • [R_{equivelent} = R_1 + R_2]
  • [L_{equivelent} = L_1 + L_2]
  • [I_{equivelent} = I_1 + I_2]
  • [V_{equivelent} = V_1 + V_2]
• and it follows
• [R_{equivelent} = \rho \frac{ L_1 + L_2}{ A}]

Qurestion 2

Two resistors, one having half the resistance of the other, are connected to a battery as shown.

What is the voltge across the bigger resistor?

• [ \frac{ 2 V_B}{ 3}]
  • Since the current through both resistors is the same, and since Ohm's Law [V = I R] is true for each one, we know that the voltage agross the bigger resistor is twice as big as the voltage across the smaller one. This means that the voltage across the bigger resistor is two thirds of [V B] and the voltage across the smaller resistor is one third of [V B].

Resistors in Parallel

• Cruuent leaving a battery must split into the two resistors

  • [I = I_1 + I_2]
  • What determines how much current goes through each of the resistors is each of the resistors have an equal voltage drop
    • [V_b = V_1 = V_2]
  • Hence [I_b = \frac{ V_b}{ R_1} + \frac{ V_b}{ R_2}]

• [\frac{ 1}{ R_{equivelent}} = \frac{ 1}{ R_1} + \frac{ 1}{ R_2}]

• [I_{equivelent} = I_1 + I_2]

• [V_{equivelent} = V_1 = V_2]

Comparison with Capacitors

• [C_{series} = \frac{ 1}{ C_1} + \frac{ 1}{ C_2}]
• [R_{serire} = R_1 + R_2]
• [C_{parallel} = C_1 + C_2]
• [R_{Parallel} = \frac{ 1}{ R_1} + \frac{ 1}{ R_2}]

Power

• [P = I V] or [P = I^2 R]
  • [P = \frac{ d U}{ d t}]
  • [d U = dq V]
    • [d q = I d t]
  • [d U = I d t V]
  • [P = \frac{ d U}{ d t} = I V]
    • Valid for any device which [I] flows accross a potential difference [V]
• SI Unit is the Watt which is equal to Volt-Apere
  • [W = V A]

Summary

• Electric Current
  • [I \equiv \frac{ d q}{ d t}]
• Ohm's Law
  • [J = \sigma E]
    • where [\sigma] is conductivity
  • [V = I R]
    • found by characiterizing the resistance [R = \frac{ 1}{ \sigma} \frac{ L}{ A}]
• Resistors in series
  • [R_{serire} = R_1 + R_2]
• Resistors in parallel
  • [R_{Parallel} = \frac{ 1}{ R_1} + \frac{ 1}{ R_2}]
• Power
  • [P = I V]