prelecture_10_kirchoffs_rule

Kirchhoff's Rules

Overview

• Start with a brief overview of the devices we will using
  • Switch
    • 
  • Battery
    • 
  • Capacitor
    • 
  • Resistor
    • 
• Then we will introduce Kirchoff's Rule
  • [\sum \Delta V_n = 0]
    • any closed loop
  • [\sum I_in = \sum I_out]
    • at any node
• Close by modeling a real battery as an ideal battery in series

Review of Electrical Devices

• Battery
  • Maintain a constant potential difference across their terminals
    • sometimes this potential difference is referred to as the EMF
    • [EMF \equiv \varepsilon = V_b]
  • 
• Capacitors
  • Capacitors store charge
  • [V_C = \frac{ Q}{ C}]
    • the voltage drop accross capacitors is equal to excess charge [Q] on one plate divided by [C] it's capacitance.
    • We speak about capacitors in terms of the rate of change across it's plates.
  • 
• Resistors
  • The voltage drop across resistors is proportional to current that flows through it.
  • [V_R = I R]
  • 
• Switch
  • Used to add or remove other devices from the circuit.
    • When the switch is open no current passes through it when the switch is close current passes freely through it. and the voltage across the switch is zero.
  • 

Kirchoff's Rules

• Voltage Rule
  • [\sum \Delta V_n = 0]
  • If you start on any point in a circuit and follow that around a complete loop the net change in the electric potential is zero.
  • 
• Current Rule
  • [\sum I_{in} = \sum I_{out}]
  • Essentially a statement of charge conservation, at any node in a circuit a place where two or more wires meet, the sum of the currents flowing in is equal to the sum of the currents flowing out.
  • 

Conventions

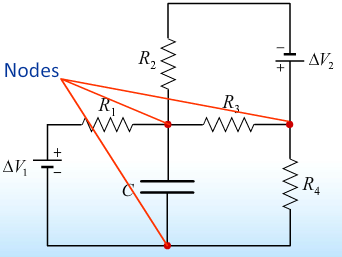
• In order to apply these two rules to circuits we must first address the issue of sign convention. In particular we need to address the conventions for the direction of current flow and the sign in which the voltage changes.
• One loop circuit
  • 
  • It doesn't matter which way you go ultimately the change in potential is zero.
  • For historical reason we will go clockwise around the loop
  • we define [\Deslta V_{R_1} = + V_{R_1}] to be positive across resistors.

Single Loop Example

• Again looking at a single loop
  • 
  • As we move around the loop from point a to point b we encounter a voltage drop. Which is equal to the product of the current and the resistance.
    • [\Delta V_{R_1} = + I R_1]
    • [\Delta V_{R_2} = + I R_2]
    • [\DELTA V_{batter} = - V_b]
    • Hence [\sum \Delta V_n = I R_1 + I R_2 + (- V_b) = 0]
    • As expected we find that [I = \frac{ V_b}{ R_1 + R_2}] * This follows that the direction is clockwise.

Two loop example

• We now look at a two loop example.
  • 
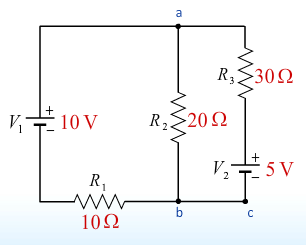
  • Analyzing the loops we find three equations and three unknowns.
    • [I_1 + I_2 = I 3] kirchoff's current rule
    • [I_3 R_3 + V_2 + I_1 R_1 - V_1 = 0] outer loop
    • [-I_2 R_2 + I_1 R_1 - V_1 = 0]
    •