Recreación de los algoritmos mas populares y utilizados, hechos y explicados en python!
- Python 3.10
- NetworkX (Visualización de gráficos)
- Matplotlib (Visualización de gráficos)
- La utilización de módulos de terceros networkX y matplotlib no son necesarios para el funcionamiento del código por lo tanto estos pueden ser removidos, sin embargo estos sirven para darnos una ayuda visual sobre el grafo.
- Las complejidades indicadas en este archivo siempre son teniendo en cuenta los peores casos de los algoritmos.
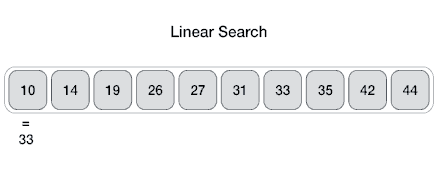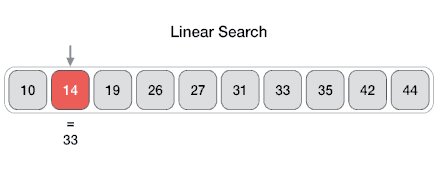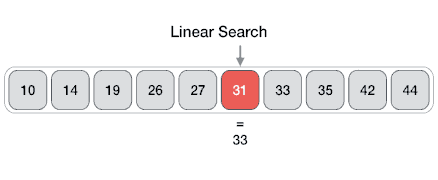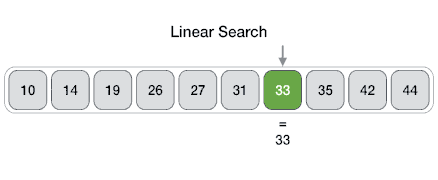
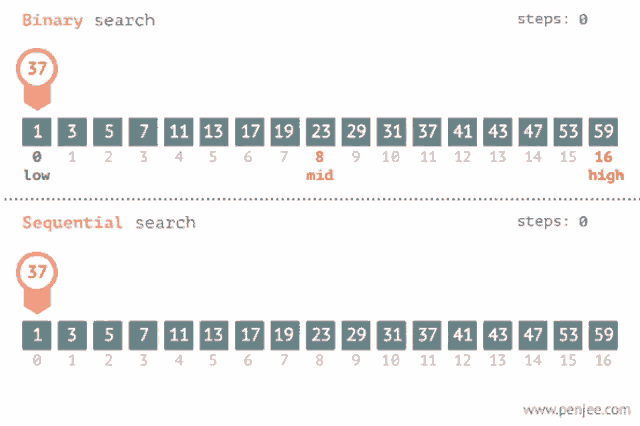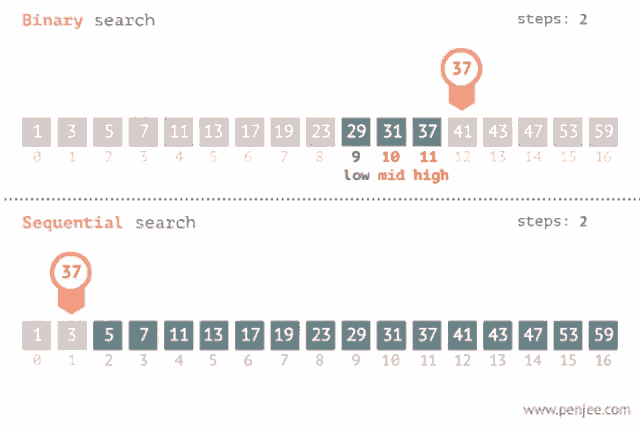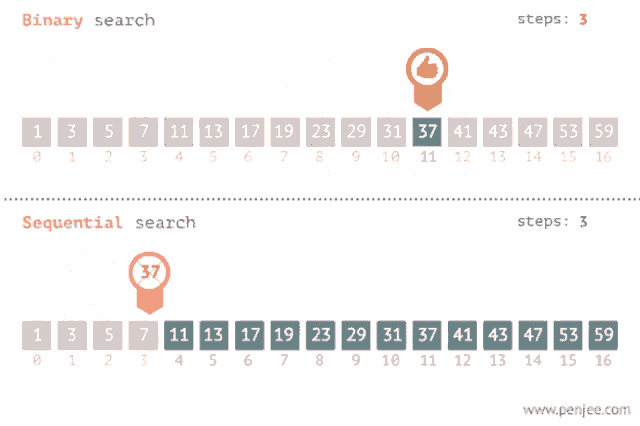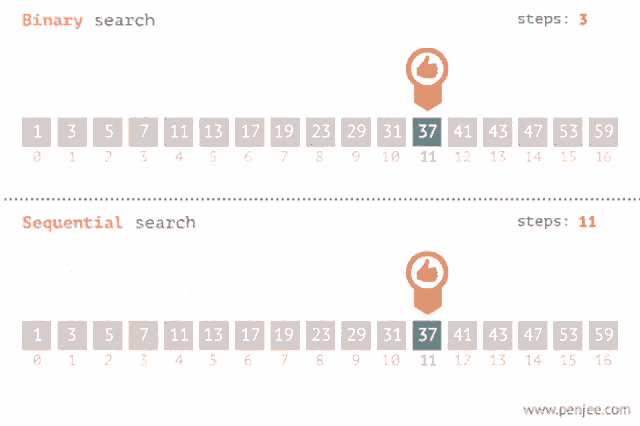
Es un método para encontrar un valor dentro de una lista (vector), en este método comprobamos de manera secuencial cada elemento para ver si coincide con el que estamos buscando o hasta que todos los elementos hayan sido comparados. Su complejidad es O(n).
Sirve también para encontrar un valor dentro de una lista pero esta debe estar ordenada, lo que hace es ir comparando con el elemento en el medio del array, si no son iguales la mitad en el cual el valor no puede estar es eliminada y la búsqueda continua en la mitad hasta que el valor se encuentre o se termine de recorrer el array. Su complejidad es O(log n).
Recomendación: Aquí te dejo un link donde podrás visualizar como se realiza tanto una búsqueda binaria como una lineal: Search visualization
Es un algoritmo para recorrer todos los nodos de un grafo o árbol de manera ordenada pero no uniforme, va expandiendo y visitando todos los nodos de forma recurrente de un camino, cuando este se queda sin nodos regresa y repite el proceso con los hermanos del nodo ya procesado. Este método se puede pensar como una pila. Su complejidad es O(V + E) siendo V el numero de vertices y E el numero de aristas(edge). Su procedimiento seria el siguiente:
- Apilo el vértice inicial.
- Lo marco como visitado y lo quito de la pila.
- Añado a la pila a sus vecinos y visito alguno de ellos.
- Repito desde el punto 2, en caso de no tener ningún vecino ya que este es el ultimo puedo seguir con alguno de la pila.
Recomendación: DFS visualization
Este método es parecido al anterior solo que en este caso vamos a pensarlo como una cola. Complejidad O(V + E). Su procedimiento seria el siguiente:
- Encolo el vértice inicial.
- Lo marco como visitado y lo quito de la cola.
- Añado a la cola a sus vecino y visito alguno de ellos.
- Repetir desde el punto 2, en caso de no tener ningún vecino puedo seguir con los de la cola.
Recomendación: BFS visualization
- In-place/Out-place -> Normalmente cuando nos referimos a algoritmos in place quiere decir algoritmos que su complejidad en el espacio es muy baja, en resumen: Algoritmos que usan poco almacenamiento.
- Recursion -> Algunos algoritmos pueden ser recursivos o no recursivos, hay algunos que incluso son los dos (merge sort).
- Estabilidad -> Un algoritmo estable es aquel que cuando hay elementos con claves iguales después de ordenarlos estos mantienen su orden relativo.
Es un método sencillo de ordenamiento, este compara cada elemento de la lista con el siguiente, si esta en el orden equivocado lo cambia de posición hasta que finalmente este en la posición correcta y luego repite el proceso con los demás números de la lista, es un algoritmo estable y también es in-place, se suele utilizar para aprender algoritmos de ordenamiento debido a su simpleza. Su complejidad es O(n^2)
Método sencillo de ordenamiento, es mas parecido a como ordenaría un humano por ejemplo un mazo de cartas. Lo que hace este método es ir comparando cada elemento de la lista con los métodos ya ordenados, de esta manera si encuentra un elemento menor o ya no encuentra elementos se tiene y pasa a repetir el proceso con el siguiente elemento, es un algoritmo estable y in-place, se suele utilizar en listas pequeñas o listas grandes que ya estén casi ordenadas. Su complejidad es O(n^2)
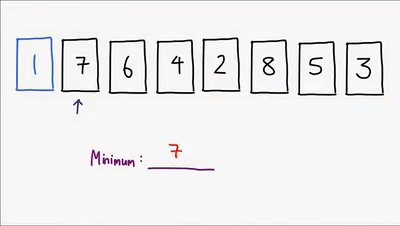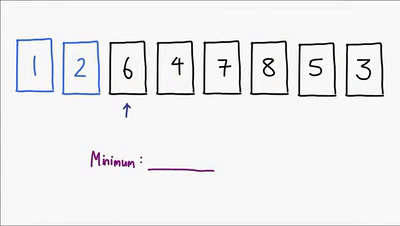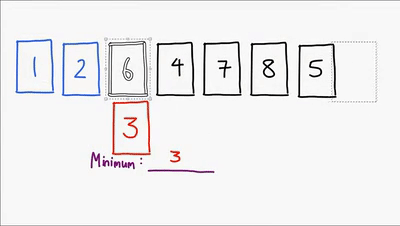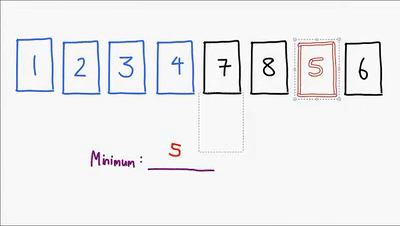
Ultimo método sencillo de ordenamiento, este ordena la lista comparando cada elemento para encontrar siempre el mínimo de los elementos no ordenados y asi finalmente lograr ordenar la lista, es un algoritmo no estable aunque hay implementaciones que lo hacen ser estable, es in-place, es util para cuando el vector esta casi ordenado. Su complejidad es O(n^2)
Este método de ordenamiento basado en la técnica divide and conquer(divide y vencerás).Es un algoritmo estable y y también out-place aunque hay una version in-place, suele ser recursivo, este algoritmo es util para ordenar listas enlazadas o cuando necesitas hacer external sorting osea ordenar grandes cantidades de datos.Su complejidad es de O(n log n). Su funcionamiento es el siguiente:
- Dividir la lista en dos subsistas "dividiéndola a la mitad"
- Ordenas cada subsista de manera recursiva aplicando merge sort
- Mezclas las dos subsistas en una lista ordenada
Es uno de los métodos de ordenamientos mas rápidos, a veces puede ser mas rápido que merge sort y dos o tres veces mas rápido que heapsort. Es un organismo de divide and conquer(divide y vencerás). Hay dos tipos de manera de tomar la partición en este quicksort, esta la partición de Hoare y la de Lomuto, sus diferencias son que la de Hoare es mas compleja y utiliza y por lo tanto mas eficiente. En el algoritmo de Hoare se suele tomar como pivote inicial el primero mientras que en el de Lomuto se suele tomar el ultimo. Este algoritmo suele ser no estable aunque hay implementaciones para hacerlo estable, es in-place, normalmente se suele utilizar para ordenar arrays a diferencia del mergesort que se usa para listas enlazadas. Su complejidad en el peor de los casos es O(n^2) que esto va a ser cuando el array ya esta ordenado o prácticamente ordenado, sin embargo en promedio suele tomar O(n log n). Su funcionamiento seria el siguiente:
- Se toma como pivote el ultimo elemento.
- Desde la izquierda se toma el primer elemento que es mas grande que el pivote
- Desde la derecha se toma el primer elemento que es mas chico que el pivote
- Se hace un swap
- Se repite desde 2. Pero si el item de la derecha se pasa significa que ya completamos por lo tanto hacemos un ultimo swap del item de la izquierda con el pivote.
- Ahora vamos a tener una lista dividida en dos partes a la izquierda y derecha del pivote, en cada nueva lista aplico desde el item 1 hasta que quede una lista con 1 elemento.
Demostración con el método de Hoare
¿Seguís sin entenderlo? Quizás este video pueda ayudarte
Es un algoritmo de ordenamiento en el cual se cuenta el número de elementos de cada clase para ordenarlos, solo puede ser utilizado por elementos contables (enteros). La version original del counting sort no puede ser utilizada para ordenar una lista con números negativos sin embargo hay una version que mejora esto. Este algoritmo suele ser no-estable, es out-place. Su complejidad es O(n + k) siendo k la cantidad de números no negativos. Su funcionamiento es el siguiente:
- Se busca el mínimo y el máximo de la lista
- Se crea un vector auxiliar
- Se recorre la lista de números y se cuenta los elementos, ejemplo si el numero 2 esta 4 veces en la lista entonces en el vector_auxiliar[2] = 4
- Recorro el vector auxiliar y asi obtengo la lista ordenada
Consiste en aprovechar las propiedades del árbol heap el cual siempre en su nodo raíz tendrá el elemento de mayor valor, por lo tanto solo tenemos que ir extrayendo siempre su raíz, luego de cada extracción el algoritmo pone en su nueva raíz a la ultima hoja derecha por el ultimo nivel (Lo cual hace que deje de ser un heap) pero mediante sift-down(el cual recupera la propiedad de heap) o sift-up este puede volver a utilizarse. Recordar que este algoritmo no puede ser utilizado directamente sobre una lista ya que esta debe pasar por un proceso de heapify(convertirlo en heap) antes. Es un algoritmo no estable y in-place, este algoritmo puede ser util cuando nos queremos garantizar una complejidad O(n log n) ya que quicksort no la garantiza y a su vez cuando queremos garantizar no usar memoria extra como es en el merge sort.Su complejidad es O(n log n)