To run the double penduluum simulation
python3 doublePenduluum.py (Runtime prior to animation is about a few seconds)
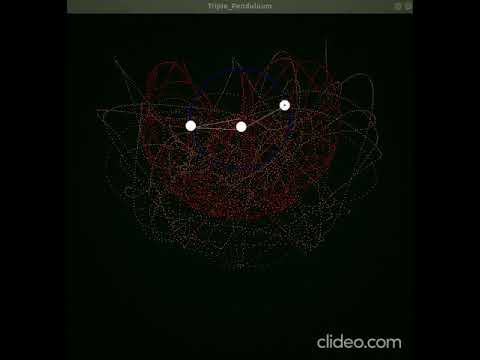
To run the triple penduluum simulation (Runtime prior to animation is about 1 minute)
python3 TriplePenduluum.py
To run the quadruple penduluum simulation (Runtime prior to animation is many hours)
python3 quadPenduluum.py
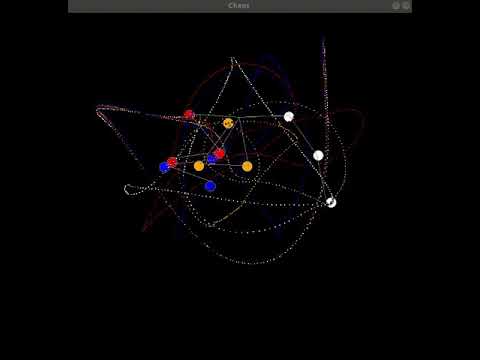
To see multiple triple penduluums with slightly diffrent initial conditions run python3 chaos.py (Runtime prior to animation is about 1 minute)
This is an image at the start of the simulation. There are 4 triple penduluums. Each has a slightly diffrent angle to it's first mass.
This is the system a fraction of a second later. You can already see the error growing
A few seconds later the penduluum's trajectories have completly diverged
This is the system way later! Havoc has been wreaked!
Link to video (Use 720 hd)
The triple penduluum is extremly sensitive to perturbations!! Don't believe me? Run my code and see how quickly slight diffrences in the initial conditions leads to very diffrent trajectories.
A really awesome surprise was how cool the trajectory plotted over time looked! Here is a picture. This could realy make for a cool screensaver
Link to the video (Use 720 hd)
I used sympy to solve the equations of motion symbolically. This is fine for the single, double, and triple penduluum but becomes an unreasonable approach when you go beyond three penduluums. I should try solving numerically and see how the performace compares. It should be dramatically faster.