sort_merge_join.md

Sort-Merge Join

Basic Strategy

Approach:

• Sort both relations on join attribute.
• Scan together using merge to form result (r, s) tuples.

Advantages:

• No need to deal with all S tuples for each r tuples.
• Deal with runs of matching R and S tuples.

Disadvantages:

• Cost of sorting both relations.
• Some rescanning required when long runs of S tuples.

Algorithm

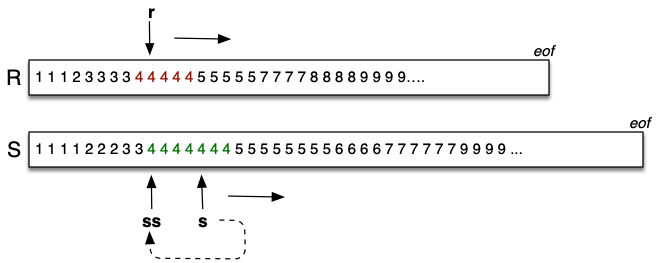
Merging for join requires 3 cursors to scan sorted relations:

• r = current record in R relation.
• s = current record in S relation.
• ss = start of current run in S relation.

ri: Query = startScan("SortedR")
si: Query = startScan("SortedS")

while (r := nextTuple(ri)) is not None \
        and (s := nextTuple(si)) is not None:
    # aligns cursors to start of next common run
    while r is not None and r.i < s.j:
        r = nextTuple(ri)

    if r is None:
        break

    while s is not None and r.i > s.i:
        s = nextTuple(si)

    if s is None:
        break

    # must have r.i == s.i here

    startRun: TupleId = scanCurrent(si)
    x

    while r is not None and r.i == s.j:
        while s is not None and s.j = r.i:
            addTuple(outBuf, combine(r, s))
            if isFull(outBuf):
                writePage(outFile, outp, outBuf)
                outp += 1
                clearBuf(outBuf)

            s = nextTuple(si)
        r = nextTuple(ri)
        setScan(si, startRun)

Buffer Requirements

Sort phase:

• As many as possible (cost is O(log(N))).
• If insufficient buffers, sorting cost can dominate.

Merge phase:

• 1 output buffer for result.
• 1 input buffer for relation R.
• (Preferably) enough buffers for longest run in S.

Cost

Step 1: sort each relation (if not already sorted):

• Cost = 2 * b_r * (1 + ceil(log_{N - 1}(b_R / N))) + 2 * b_s * (1 + ceil(log_{N - 1}(b_RS/ N)))
• N is number of memory buffers.

Step 2: merge sorted relations:

• If every run of values in S fits completely in buffers, merge requires single scan.
  • Cost = b_R + b_S.
• If some runs in S are larger than buffers, need to re-scan run for each corresponding value from R.
  • Need to re-scan old values of S for new value of R.