This article is not an article explaining data structures, but a combination of real-world scenarios to help you `understand and review' data structures and algorithms. If your data structure foundation is poor, it is recommended to go to some basic tutorials first, and then turn around.
The positioning of this article focuses on the front-end. By learning the data structure of the actual scene in the front-end, we can deepen everyone's understanding and understanding of the data structure.
We can logically divide data structures into linear structures and nonlinear structures. Linear structures include arrays, stacks, linked lists, etc., while non-linear structures include trees, graphs, etc.
It should be noted that linearity and non-linearity do not mean whether the storage structure is linear or non-linear. There is no relationship between the two, it is just a logical division. For example, we can use arrays to store binary trees. Generally speaking, linear data structures are the forerunners and successors. For example, arrays and linked lists.
In fact, many of the data structures behind have the shadow of arrays. Arrays are the simplest data structure, and they are used in many places. For example, if you use a data list to store some user ids, you can use arrays to store them.
The stacks and queues that we will talk about later can actually be regarded as a kind of restricted arrays. How about the restricted method? We will discuss it later.
Next, we will use a few interesting examples to deepen everyone's understanding of the data structure of arrays.
The essence of Hooks is an array, pseudo-code:
So why do hooks use arrays? We can explain from another perspective, what would happen if we didn't use arrays?
function Form() {
// 1. Use the name state variable
const [name, setName] = useState("Mary");
// 2. Use an effect for persisting the form
useEffect(function persistForm() {
localStorage.setItem("formData", name);
});
// 3. Use the surname state variable
const [surname, setSurname] = useState("Poppins");
// 4. Use an effect for updating the title
useEffect(function updateTitle() {
document.title = name + " " + surname;
});
// . . .
}Based on the array method, the hooks of Form are [hook1, hook2, hook3, hook4].
From then on, we can draw such a relationship. hook1 is the pair of [name, setName], and hook2 is the persistForm.
If you don't use arrays to implement, such as objects, the hooks of Form are
{
'key1': hook1,
'key2': hook2,
'key3': hook3,
'key4': hook4,
}So the question is how to take key1, key2, key3, and key4? This is a problem. For more research on the nature of React hooks, please check React hooks: not magic, just arrays
However, there is also a problem with using arrays. That is, React has left the task of `how to ensure the correspondence between the states saved by Hooks inside the component'to the developer to ensure, that is, you must ensure that the order of hooks is strictly consistent. For details, please refer to React's official website in the Hooks Rule section.
A queue is a kind of restrictedsequence. Where is the restriction? Restricted is restricted in that it can only manipulate the end of the team and the beginning of the team, and can only add elements at the end of the team and delete elements at the beginning of the team. Arrays do not have this restriction.
Queues, as one of the most common data structures, are also widely used, such as message queues.
The name "queue" can be analogous to queuing in real life (the kind that does not cut in line)
In computer science, a queue is a special type of abstract data type or collection, and the entities in the collection are stored in order.
There are two basic queue operations:
-Add an entity to the backend location of the queue, which is called queuing -Removing an entity from the front end of the queue is called dequeue.
Schematic diagram of FIFO (first in, first out) for elements in the queue:
(Picture from https://github.com/trekhleb/javascript-algorithms/blob/master/src/data-structures/queue/README.zh-CN.md )
When we are doing performance optimization, one point that we often mention is “the header blocking problem of HTTP 1.1”. Specifically, it is that HTTP 2 solves the header blocking problem in HTTP 1.1, but many PEOPLE DON't know why THERE is a header blocking problem with HTTP 1.1 and how to solve this problem with HTTP2. It is unclear to many people.
In fact "team head blocking is a proper noun, not only in HTTP, but also in other places such as switches. This issue is also involved. In fact, the root cause of this problem is the use of a data structure called a queue.
The protocol stipulates that for the same tcp connection, all http 1.0 requests are placed in the queue, and the next request can only be sent if the previous'response to the request` is received. At this time, a blockage occurs, and this blockage mainly occurs on the client.
It's as if we are waiting for the traffic light. Even if the green light is on next to you, your lane is a red light, you still can't go, you still have to wait.
HTTP/1.0' and HTTP/1.1`:
In `HTTP/1.0', a TCP connection needs to be established for each request, and the connection is disconnected immediately after the request ends.
In "HTTP/1.1`, each connection defaults to a long connection (persistent connection). For the same tcp connection, multiple http 1.1 requests are allowed to be sent at once, that is to say, the next request can be sent without having to wait for the previous response to be received. This solves the header blocking of the client of HTTP 1.0, and this is the concept of "Pipeline" in "HTTP/1.1".
However, `http 1.1 stipulates that the transmission of server-side responses must be queued in the order in which the requests are received', that is to say, the response to the first received request must also be sent first. The problem caused by this is that if the processing time of the first received request is long and the response generation is slow, it will block the transmission of the response that has been generated, which will also cause the queue to block. It can be seen that the first queue blocking of http 1.1 occurred on the server side.
If it is represented by a diagram, the process is probably:
HTTP/2' and HTTP/1.1`:
In order to solve the server-side queue-first blocking in "HTTP/1.1", "HTTP/2" adopts methods such as "BINARY frame splitting" and "multiplexing".
The frame is the smallest unit of HTTP/2 data communication. In "HTTP/1.1", the data packet is in text format, while the data packet of "HTTP/2" is in binary format, which is a binary frame.
The frame transmission method can divide the data of the request and response into smaller pieces, and the binary protocol can be parsed efficiently. In 'HTTP/2`, all communications under the same domain name are completed on a single connection, which can carry any number of two-way data streams. Each data stream is sent in the form of a message, which in turn consists of one or more frames. Multiple frames can be sent out of order between them, and can be reassembled according to the stream identification of the frame header.
Multiplexing is used to replace the original sequence and congestion mechanism. In 'HTTP/1.1, multiple TCP links are required for multiple simultaneous requests, and a single domain name has a limit of 6-8 TCP link requests (this limit is restricted by the browser, and different browsers may not be the same). In 'HTTP/2, all communications under the same domain name are completed on a single link, occupying only one TCP link, and requests and responses can be made in parallel on this link without interfering with each other.
This website You can intuitively feel the performance comparison between 'HTTP/1.1' and`HTTP/2'.
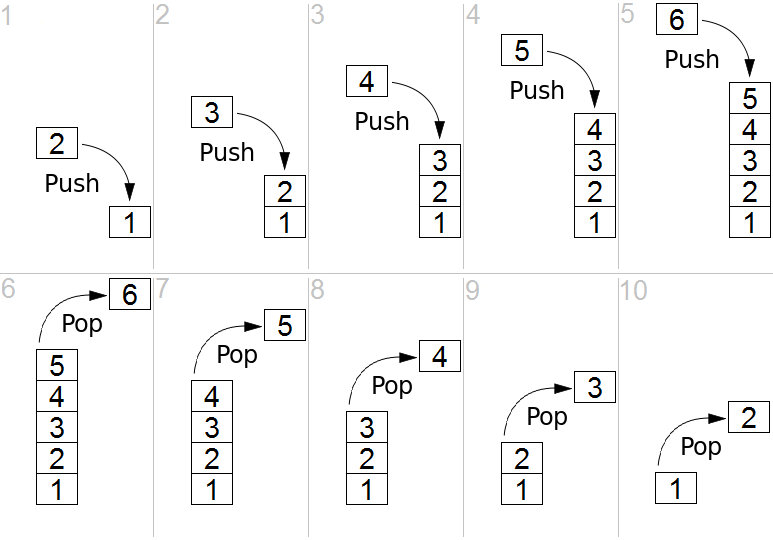
The stack is also a kind of restricted sequence. When it is restricted, it is limited to only being able to operate on the top of the stack. Regardless of whether it enters or exits the stack, it is operated on the top of the stack. Similarly, arrays do not have this restriction.
In computer science, a stack is an abstract data type that is used to represent a collection of elements and has two main operations.:
-push, add elements to the top (end) of the stack -pop, remove the element at the top (end) of the stack
The above two operations can be simply summarized as ** last in, first out (LIFO =last in, first out)**.
In addition, there should be a peek operation to access the current top (end) element of the stack. (Only return, no pop-up)
The name "stack" can be analogous to the stacking of a group of objects (a stack of books, a stack of plates, etc.).
Schematic diagram of the push and pop operations of the stack:
(Picture from https://github.com/trekhleb/javascript-algorithms/blob/master/src/data-structures/stack/README.zh-CN.md )
Stacks have applications in many places. For example, familiar browsers have many stacks. In fact, the execution stack of the browser is a basic stack structure. From the data structure point of view, it is a stack. This also explains that our recursive solution is essentially the same as the loop +stack solution.
For example, the following JS code:
function bar() {
const a = 1;
const b = 2;
console.log(a, b);
}
function foo() {
const a = 1;
bar();
}
foo();When it is actually executed, it looks like this internally:
The picture I drew does not show other parts of the execution context (this, scope, etc.). This part is the key to closure, and I am not talking about closure here, but to explain the stack.
There are many saying in the community that “scope in the execution context refers to variables declared by the parent in the execution stack”. This is completely wrong. JS is the lexical scope, and scope refers to the parent when the function is defined, which has nothing to do with execution.
Common applications of stacks are binary conversion, bracket matching, stack shuffling, infix expressions (rarely used), suffix expressions (inverse Polish expressions), etc.
Legal stack shuffling operation is also a classic topic. In fact, there is a one-to-one correspondence between this and legal bracket matching expressions. That is to say, there are as many kinds of stack shuffles for n elements, and there are as many kinds of legal expressions for n pairs of brackets. If you are interested, you can find relevant information.
Linked lists are one of the most basic data structures, and proficiency in the structure and common operations of linked lists is the foundation of the foundation.
(Picture from: https://github.com/trekhleb/javascript-algorithms/tree/master/src/algorithms/linked-list/traversal )
Many people say that fiber is implemented based on linked lists, but why should it be based on linked lists? Many people may not have the answer. Then I think we can put these two points (fiber and linked lists) together.
The purpose of fiber's appearance is actually to solve the problem that react cannot stop when it is executed, and it needs to be executed in one go.
The picture is shared by Lin Clark at ReactConf 2017
The problem before the introduction of fiber has been pointed out above, that is, react will prevent high-priority code (such as user input) from being executed. Therefore, they plan to build their own `virtual execution stack'to solve this problem. The underlying implementation of this virtual execution stack is a linked list.
The basic principle of Fiber is to divide the coordination process into small pieces, execute one piece at a time, then save the operation results, and determine whether there is time to continue to execute the next piece (react itself implemented a function similar to requestIdleCallback). If there is time, continue. Otherwise, jump out, let the browser main thread take a break and execute other high-priority code.
When the coordination process is completed (all the small pieces are calculated), then it will enter the submission stage and perform real side effect operations, such as updating the DOM. There is no way to cancel this process because this part has side effects.
The key to the problem is to divide the coordination process into pieces, and finally merge them together, a bit like Map/Reduce.
React must re-implement the algorithm for traversing the tree, from relying on a 'synchronous recursion model with built-in stacks' to an 'asynchronous model with linked lists and pointers`.
Andrew said this: If you only rely on the [built-in] call stack, it will continue to work until the stack is empty.
Wouldn't it be great if we could interrupt the call stack at will and manipulate the stack frame manually? This is the purpose of React Fiber. Fiber is a re-implementation of the stack, dedicated to React components. You can think of a single Fiber as a virtual stack frame.
react fiber is probably like this:
let fiber = {
tag: HOST_COMPONENT,
type: "div",
return: parentFiber,
children: childFiber,
sibling: childFiber,
alternate: currentFiber,
stateNode: document.createElement("div"),
props: { children: [], className: "foo" },
partialState: null,
effectTag: PLACEMENT,
effects: [],
};It can be seen from this that fiber is essentially an object. Use the parent, child, and sibling attributes to build a fiber tree to represent the structure tree of the component., Return, children, sibling are also all fibers, so fiber looks like a linked list.
Attentive friends may have discovered that alternate is also a fiber, so what is it used for? Its principle is actually a bit like git, which can be used to perform operations such as git revert, git commit, etc. This part is very interesting. I will explain it in my "Developing git from Scratch".
Friends who want to know more can read this article
If you can go over the wall, you can read original English
This article It is also an excellent early article on fiber architecture
I am also currently writing about the fiber architecture part of the "react Series of Tutorials for Developing react from Scratch". If you are interested in the specific implementation, please pay attention.
So with a linear structure, why do we need a nonlinear structure? The answer is that in order to efficiently balance static and dynamic operations, we generally use trees to manage data that requires a lot of dynamic operations. You can intuitively feel the complexity of various operations of various data structures.
The application of trees is also very extensive. They can be expressed as tree structures as small as file systems, as large as the Internet, organizational structures, etc., AND the DOM tree that is more familiar to our front-end eyes is also a kind of tree structure, and HTML is used as a DSL to describe the specific manifestations of this tree structure. If you have been exposed to AST, then AST is also a kind of tree, and XML is also a tree structure. The application of trees is far more than most people think.
A tree is actually a special kind of `graph', which is a kind of acutely connected graph, a maximal acutely connected graph, and a minimally connected graph.
From another perspective, a tree is a recursive data structure. Moreover, different representation methods of trees, such as the less commonly used "eldest son + brother" method, are for Your understanding of the data structure of trees is of great use, and it is not an exaggeration to say that it is a deeper understanding of the nature of trees.
The basic algorithms of the tree include front, middle and back sequence traversal and hierarchical traversal. Some students are relatively vague about the access order of the three specific manifestations of the front, middle and back. In fact, I was the same at the beginning. I learned a little later. You just need to remember: The so-called front, middle and back refer to the position of the root node, and the other positions can be arranged according to the first left and then right. For example, the pre-sequence traversal is root left and right", the middle sequence is left root right", and the post-sequence is left and right root, isn't it simple?
I just mentioned that a tree is a recursive data structure, so the traversal algorithm of a tree is very simple to complete using recursion. Fortunately, the algorithm of a tree basically depends on the traversal of the tree.
However, the performance of recursion in computers has always been problematic, so it is useful in some cases to master the not-so-easy-to-understand "imperative iteration" traversal algorithm. If you use an iterative method to traverse, you can use the'stack` mentioned above to do it, which can greatly reduce the amount of code.
If you use a stack to simplify the operation, since the stack is FILO, you must pay ATTENTION to the PUSH order of the left and right subtrees.
The important nature of the tree:
-If the tree has n nodes, then it has n-1 edges, which shows that the number of nodes and edges of the tree are of the same order. -There is a unique path from any node to the root node, the length of the path is the depth of the node
The actual tree used may be more complicated. For example, a quadtree or octree may be used for collision detection in games. And the k-dimensional tree structurek-d tree and so on.

A binary tree is a tree with no more than two nodes, and it is a special subset of trees. Interestingly, the restricted tree structure of a binary tree can represent and realize all trees., The principle behind it is the "eldest son + brother" method. In Teacher Deng's words, "A binary tree is a special case of a multi-pronged tree, but when it has roots and is orderly, its descriptive ability is sufficient to cover the latter."
In fact, while you use the "eldest son + brother" method to represent the tree, you can rotate it at an angle of 45 degrees.
A typical binary tree:
(Picture from https://github.com/trekhleb/javascript-algorithms/blob/master/src/data-structures/tree/README.zh-CN.md )
For ordinary trees, we usually traverse them, and there will be many variations here.
Below I list some related algorithms for binary tree traversal:
- 94.binary-tree-inorder-traversal
- 102.binary-tree-level-order-traversal
- 103.binary-tree-zigzag-level-order-traversal
- 144.binary-tree-preorder-traversal
- 145.binary-tree-postorder-traversal
- 199.binary-tree-right-side-view
Related concepts:
-True binary tree (the degree of all nodes can only be even, that is, it can only be 0 or 2)
In addition, I also specially opened traversal of binary trees Chapters, specific details and algorithms can be viewed there.
A heap is actually a kind of priority queue. There are corresponding built-in data structures in many languages. Unfortunately, javascript does not have this kind of native data structure. However, this will not have an impact on our understanding and application.
A typical implementation of heaps is binary heaps.
Characteristics of binary stacks:
-In a min heap, if P is a parent node of C, then the key (or value) of P should be less than or equal to the corresponding value of C. Because of this, the top element of the heap must be the smallest. We will use this feature to find the minimum value or the kth smallest value.
-In a max heap, the key (or value) of P is greater than or equal to the corresponding value of C.
It should be noted that there are not only heaps of priority queues, but also more complex ones, but generally speaking, we will make the two equivalent.
Related algorithms:
Binary Sort Tree (Binary Sort Tree), also known as Binary Search Tree (Binary Search Tree), also known as Binary Search Tree.
Binary lookup tree A binary tree with the following properties:
-If the left subtree is not empty, the value of all nodes on the left subtree is less than the value of its root node; -If the right subtree is not empty, the value of all nodes on the right subtree is greater than the value of its root node; -The left and right subtrees are also binary sorting trees; -There are no nodes with equal key values.
For a binary lookup tree, the conventional operations are to insert, find, delete, find the parent node, find the maximum value, and find the minimum value.