README.md

central-limit-theorem

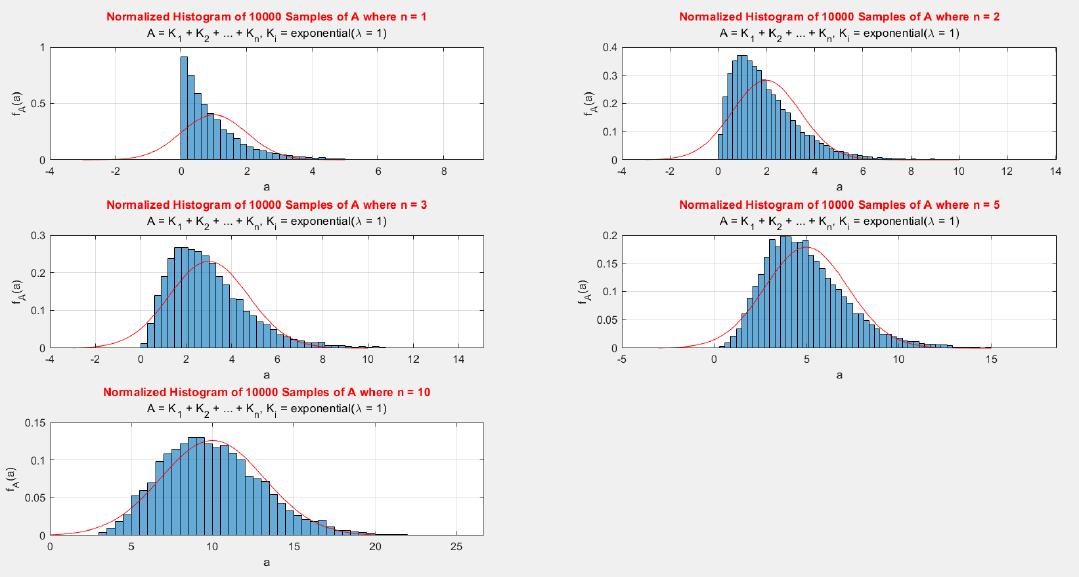
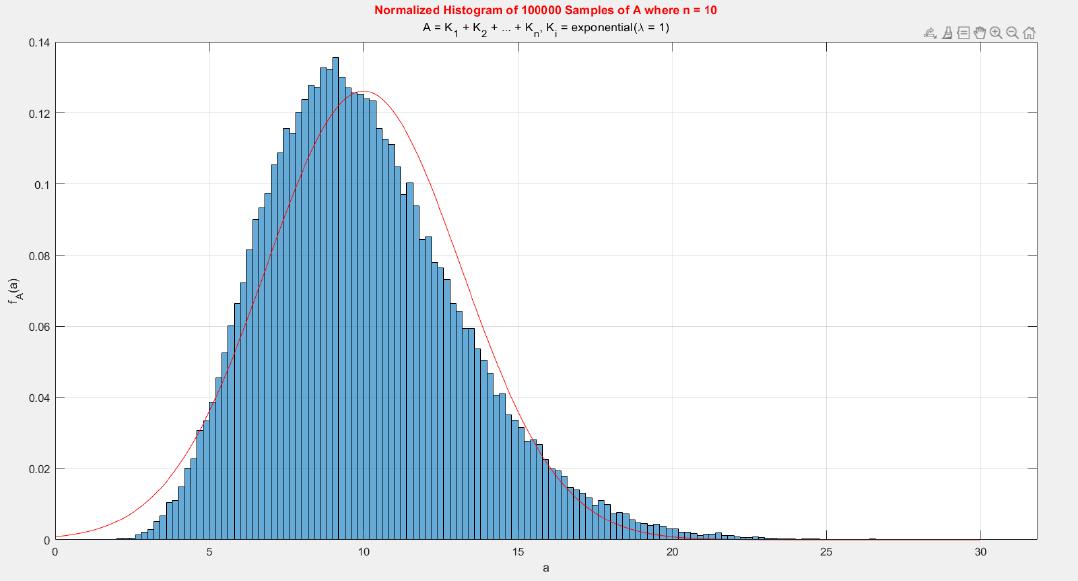
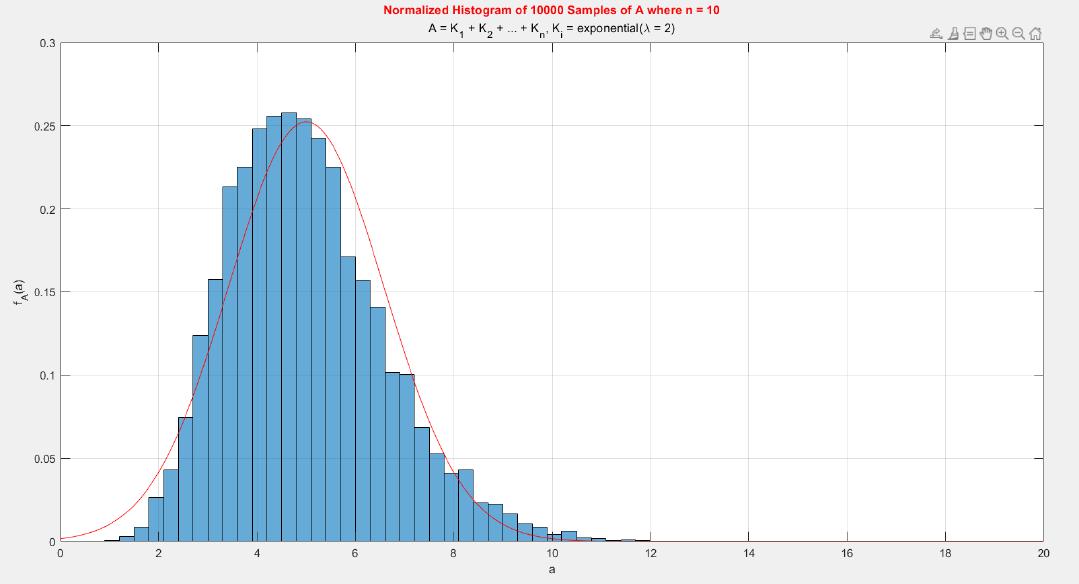
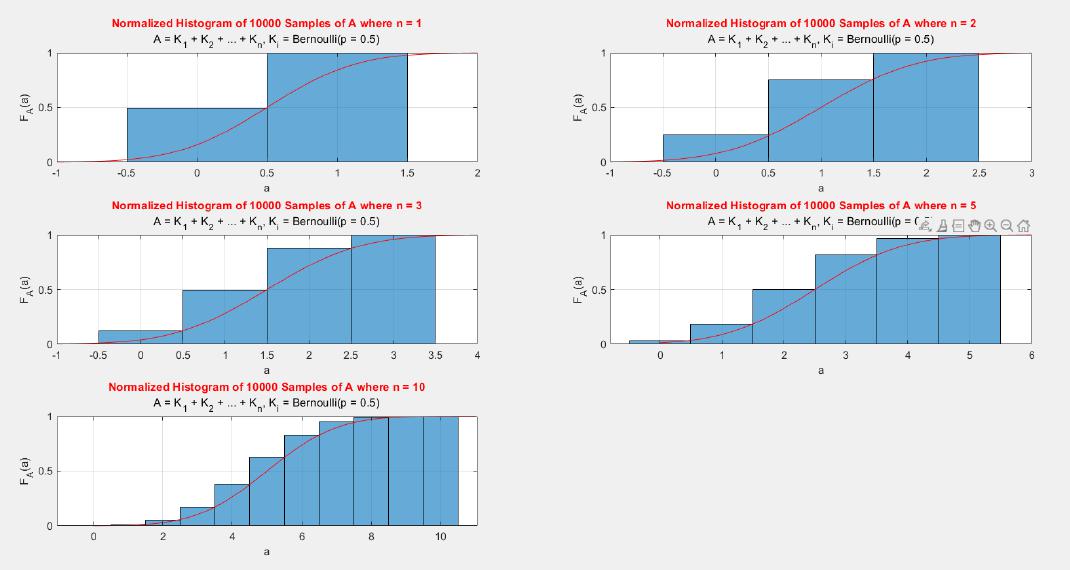
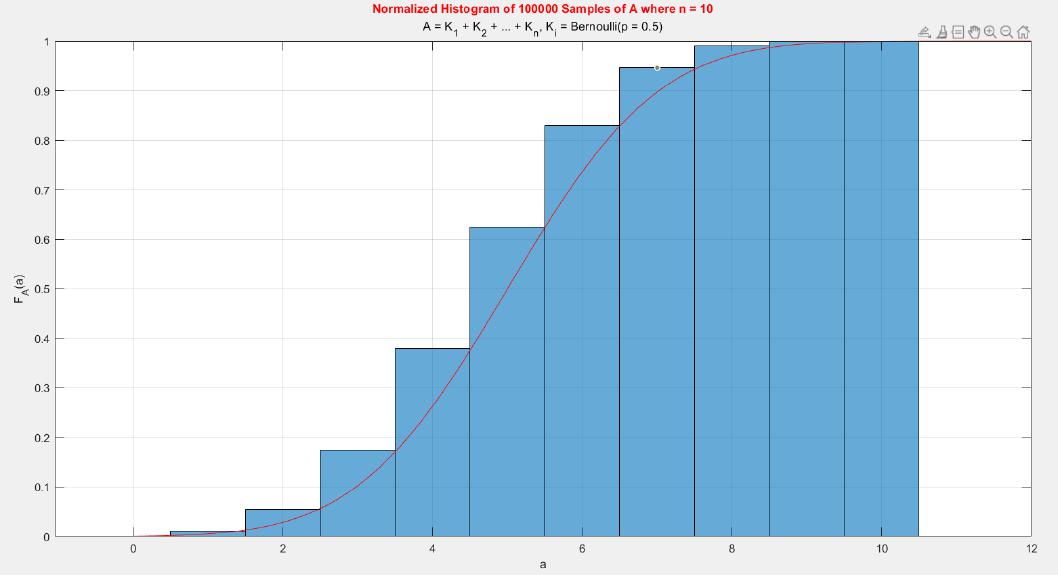
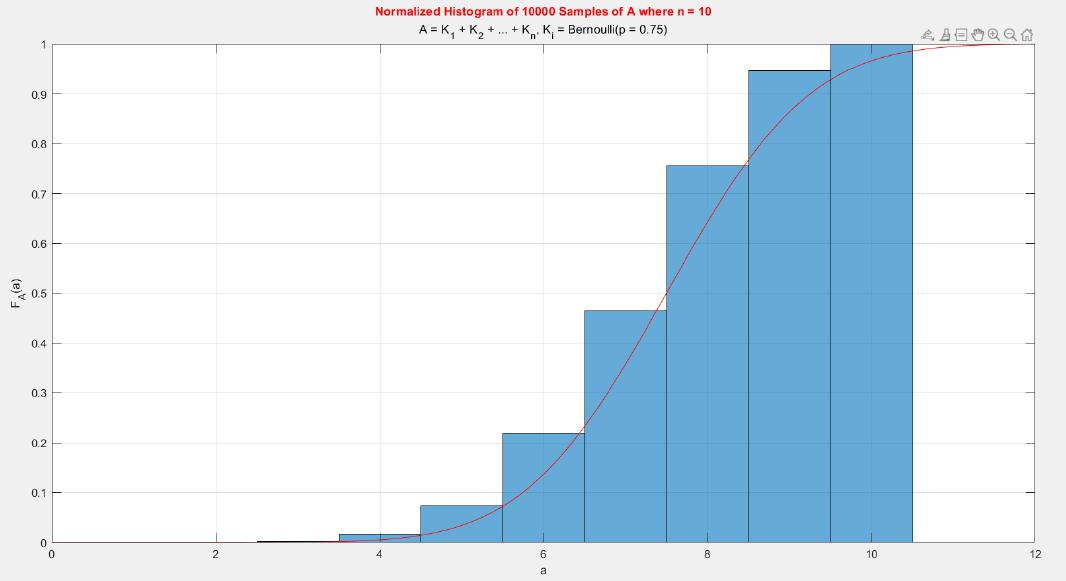
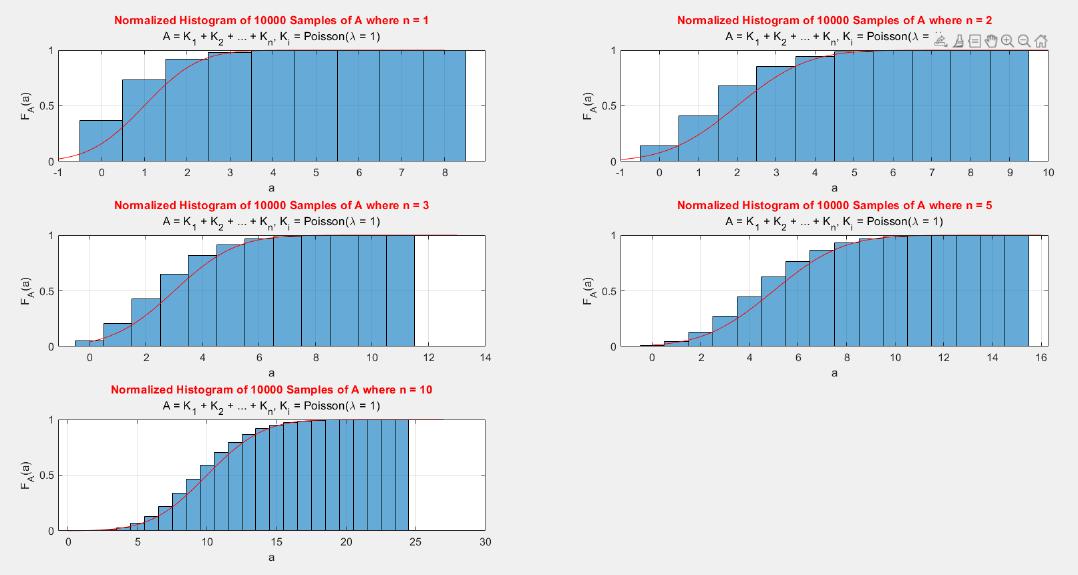
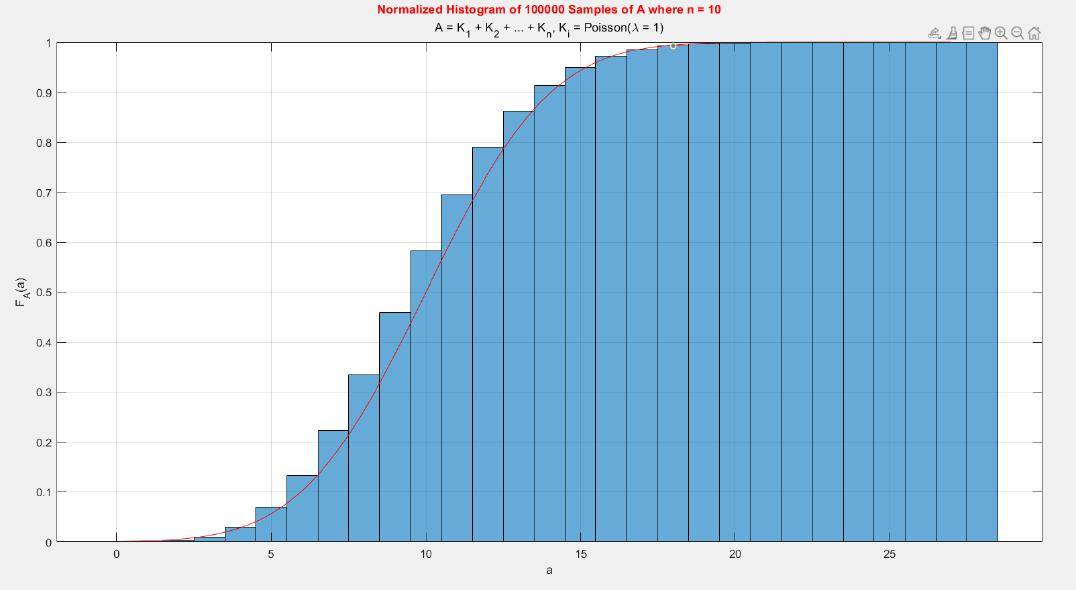
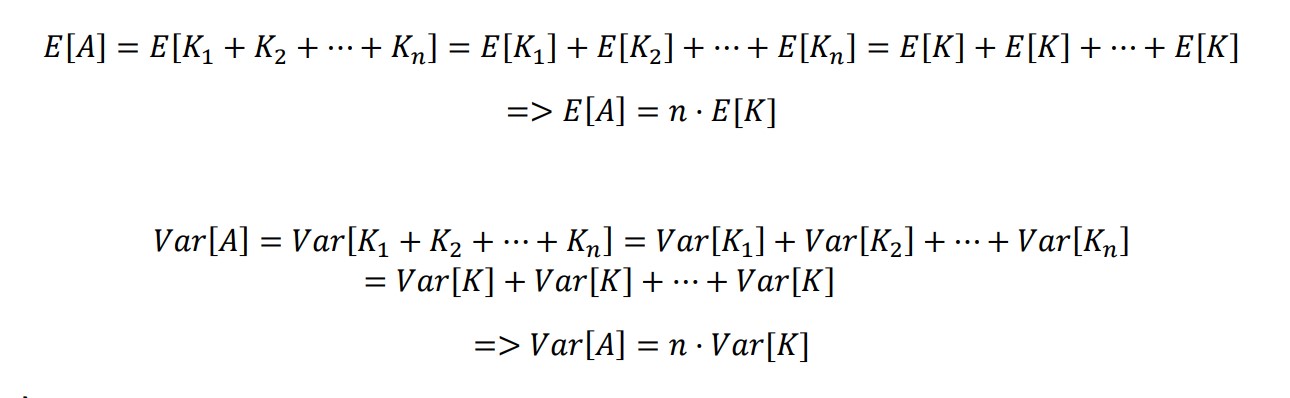A MATLAB project which applies the central limit theorem (CLT) on probability density functions (PDFs) and cumulative distribution functions (CDFs) of different probability distributions such as uniform, exponential, Bernoulli, and Poisson distribution.

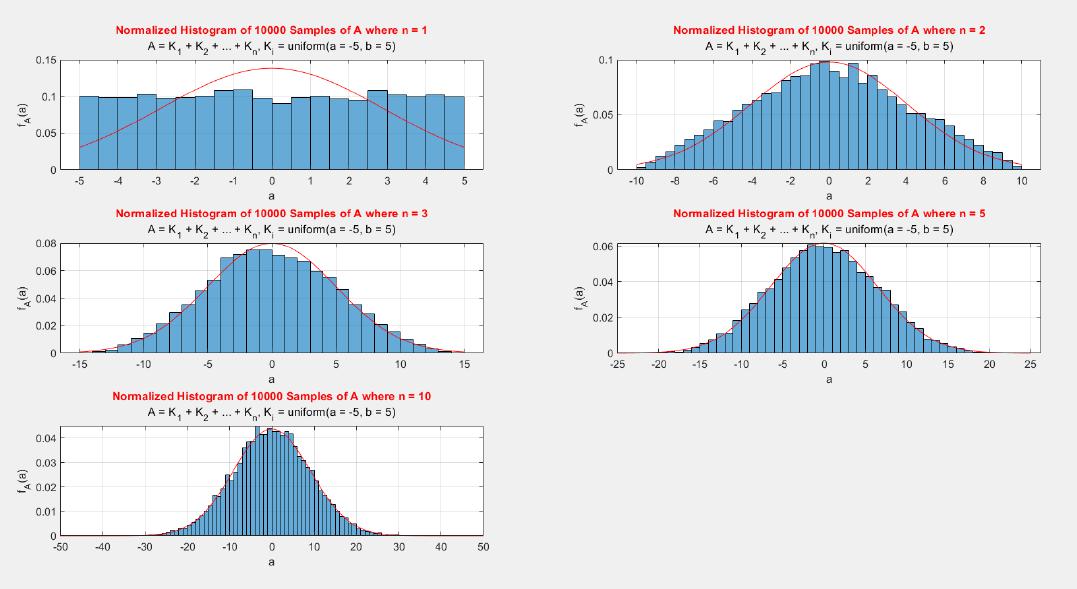
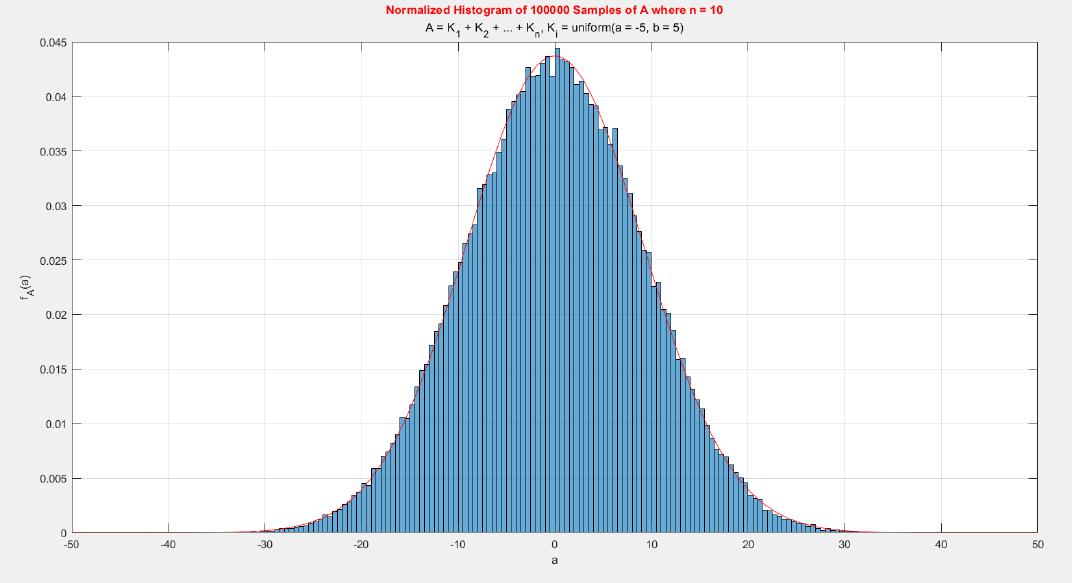
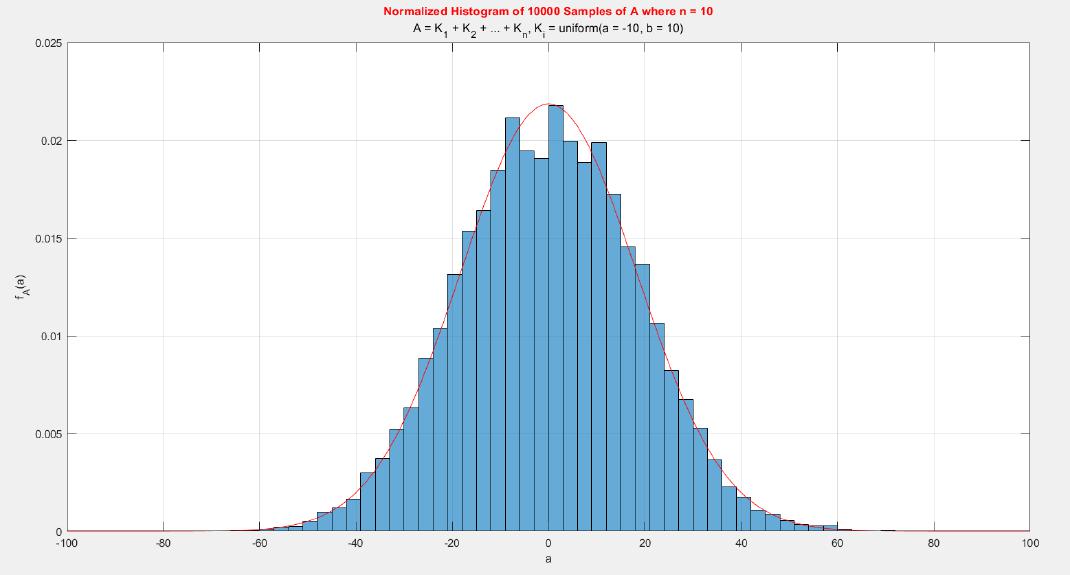
The central limit theorem (CLT) implies that given , a sequence of independent and identically distributed (IID) random variables with expected value and variance , the cumulative distribution function (CDF) of has the property . Briefly, the theorem states that as n increases, the sum of n IID random variables converges to a normal distribution.

This homework was assigned for the Probability for Electrical Engineers (EE 313) course in the Fall 2021-22 semester.

Run on Terminal

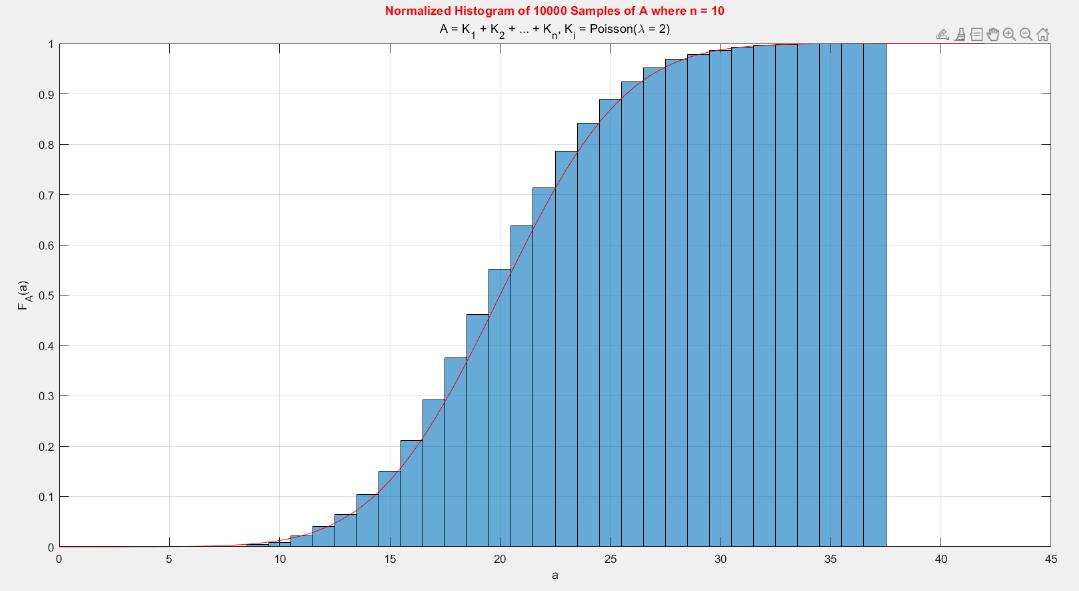
matlab -nodisplay -nosplash -nodesktop -r "run('main.m');exit;"

Proof

1) E[A] and Var[A]

𝐸[𝐴] = 𝐸[𝐾1 + 𝐾2 + ⋯ + 𝐾𝑛] =
𝐸[𝐾1] + 𝐸[𝐾2] + ⋯ + 𝐸[𝐾𝑛] =
𝐸[𝐾] + 𝐸[𝐾] + ⋯ + 𝐸[𝐾] =>
𝐸[𝐴] = 𝑛 · 𝐸[𝐾]

𝑉𝑎𝑟[𝐴] = 𝑉𝑎𝑟[𝐾1 + 𝐾2 + ⋯ + 𝐾𝑛] =
𝑉𝑎𝑟[𝐾1] + 𝑉𝑎𝑟[𝐾2] + ⋯ + 𝑉𝑎𝑟[𝐾𝑛] =
𝑉𝑎𝑟[𝐾] + 𝑉𝑎𝑟[𝐾] + ⋯ + 𝑉𝑎𝑟[𝐾] =>
𝑉𝑎𝑟[𝐴] = 𝑛 · 𝑉𝑎𝑟[𝐾]

Figures

2) Uniform PDF

3) Exponential PDF

4) Bernoulli CDF

5) Poisson CDF

Author

👤 Aras Güngöre

• LinkedIn: @arasgungore
• GitHub: @arasgungore