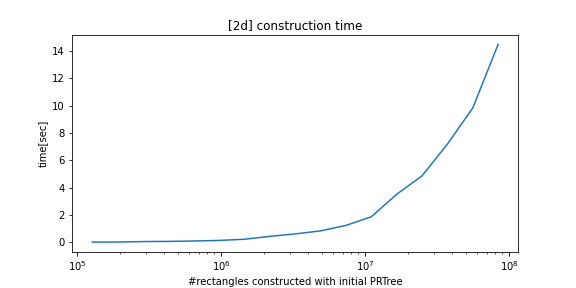
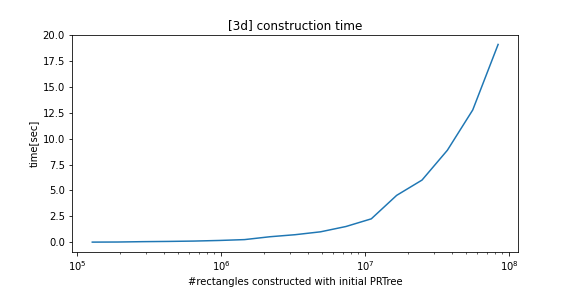
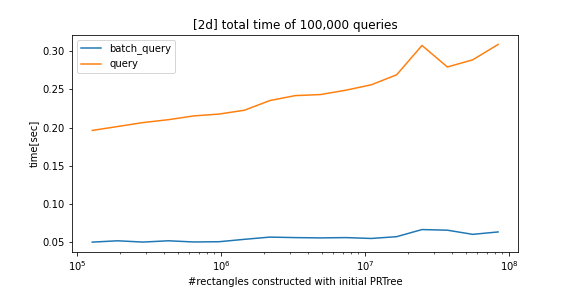
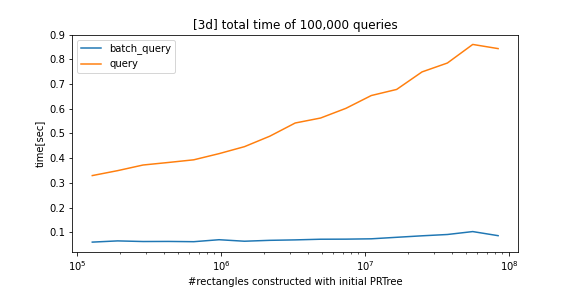
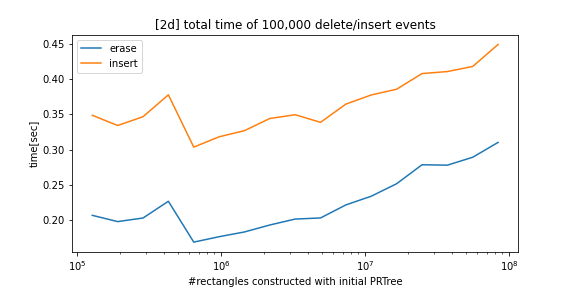
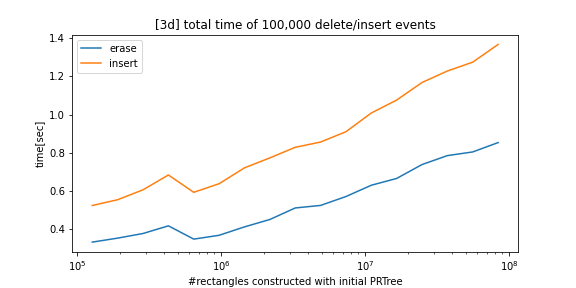
python_prtree

python_prtree is a python/c++ implementation of the Priority R-Tree (see references below), an alternative to R-Tree. The supported futures are as follows:

• Construct a Priority R-Tree (PRTree) from an array of rectangles.
  • PRTree2D, PRTree3D and PRTree4D (2D, 3D and 4D respectively)
• insert and erase
  • The insert method can be passed pickable Python objects instead of int64 indexes.
• query and batch_query
  • batch_query is parallelized by std::thread and is much faster than the query method.
  • The query method has an optional keyword argument return_obj; if return_obj=True, a Python object is returned.
• rebuild
  • It improves performance when many insert/delete operations are called since the last rebuild.
  • Note that if the size changes more than 1.5 times, the insert/erase method also performs rebuild.

This package is mainly for mostly static situations where insertion and deletion events rarely occur.

Installation

You can install python_prtree with the pip command:

pip install python-prtree

If the pip installation does not work, please git clone clone and install as follows:

pip install -U cmake pybind11
git clone --recursive https://github.com/atksh/python_prtree
cd python_prtree
python setup.py install

Examples

import numpy as np
from python_prtree import PRTree2D

idxes = np.array([1, 2])

# rects is a list of (xmin, ymin, xmax, ymax)
rects = np.array([[0.0, 0.0, 1.0, 0.5],
                  [1.0, 1.5, 1.2, 3.0]])

prtree = PRTree2D(idxes, rects)


# batch query
q = np.array([[0.5, 0.2, 0.6, 0.3],
              [0.8, 0.5, 1.5, 3.5]])
result = prtree.batch_query(q)
print(result)
# [[1], [1, 2]]

# You can insert an additional rectangle by insert method,
prtree.insert(3, np.array([1.0, 1.0, 2.0, 2.0]))
q = np.array([[0.5, 0.2, 0.6, 0.3],
              [0.8, 0.5, 1.5, 3.5]])
result = prtree.batch_query(q)
print(result)
# [[1], [1, 2, 3]]

# Plus, you can erase by an index.
prtree.erase(2)
result = prtree.batch_query(q)
print(result)
# [[1], [1, 3]]

# Non-batch query is also supported.
print(prtree.query([0.5, 0.5, 1.0, 1.0]))
# [1, 3]

# Point query is also supported.
print(prtree.query([0.5, 0.5]))
# [1]
print(prtree.query(0.5, 0.5))  # 1d-array
# [1]

import numpy as np
from python_prtree import PRTree2D

objs = [{"name": "foo"}, (1, 2, 3)]  # must NOT be unique but pickable
rects = np.array([[0.0, 0.0, 1.0, 0.5],
                  [1.0, 1.5, 1.2, 3.0]])

prtree = PRTree2D()
for obj, rect in zip(objs, rects):
    prtree.insert(bb=rect, obj=obj)

# returns indexes genereted by incremental rule.
result = prtree.query((0, 0, 1, 1))
print(result)
# [1]

# returns objects when you specify the keyword argment return_obj=True
result = prtree.query((0, 0, 1, 1), return_obj=True)
print(result)
# [{'name': 'foo'}]

The 1d-array batch query will be implicitly treated as a batch with size = 1. If you want 1d result, please use query method.

result = prtree.query(q[0])
print(result)
# [1]

result = prtree.batch_query(q[0])
print(result)
# [[1]]

You can also erase(delete) by index and insert a new one.

prtree.erase(1)  # delete the rectangle with idx=1 from the PRTree

prtree.insert(3, np.array([0.3, 0.1, 0.5, 0.2]))  # add a new rectangle to the PRTree

You can save and load a binary file as follows.

# save
prtree.save('tree.bin')


# load with binary file
prtree = PRTree('tree.bin')

# or defered load
prtree = PRTree()
prtree.load('tree.bin')

Note that cross-version compatibility is NOT guaranteed, so please reconstruct your tree when you update this package.

Performance

Construction

2d

3d

Query and batch query

2d

3d

Delete and insert

2d

3d

New Features and Changes

python-prtree>=0.5.8

• The insert method has been improved to select the node with the smallest mbb expansion.
• The erase method now also executes rebuild when the size changes by a factor of 1.5 or more.

python-prtree>=0.5.7

• You can use PRTree4D.

python-prtree>=0.5.3

• Add compression for pickled objects.

python-prtree>=0.5.2

You can use pickable Python objects instead of int64 indexes for insert and query methods:

python-prtree>=0.5.0

• Changed the input order from (xmin, xmax, ymin, ymax, ...) to (xmin, ymin, xmax, ymax, ...).
• Added rebuild method to build the PRTree from scratch using the already given data.
• Fixed a bug that prevented insertion into an empty PRTree.

python-prtree>=0.4.0

• You can use PRTree3D:

Reference

The Priority R-Tree: A Practically Efficient and Worst-Case Optimal R-Tree Lars Arge, Mark de Berg, Herman Haverkort, and Ke Yi Proceedings of the 2004 ACM SIGMOD International Conference on Management of Data (SIGMOD '04), Paris, France, June 2004, 347-358. Journal version in ACM Transactions on Algorithms. author's page