Skip to content

Latest commit

 

History

History
279 lines (200 loc) · 14.1 KB

README.md

File metadata and controls

279 lines (200 loc) · 14.1 KB
Raw

An efficient task-space capacity calculation package for robotics and biomechanics

📢 New version of the pycapacity package is out - version v2.1! - see full changelog

📢 pycpacity JOSS paper accepted 🎉 The full review available here and the 📄 paper here

About

PyPI package Tests Docs status

What is pycapacity?

Python package pycapacity provides a set of tools for evaluating task space physical ability metrics for humans and robots, based on polytopes and ellipsoids. The aim of pycapacity is to provide a set of efficient tools for their evaluation in an easy to use framework that can be easily integrated with standard robotics and biomechanics libraries. The package implements several state of the art algorithms for polytope evaluation that bring many of the polytope metrics to the few milliseconds evaluation time, making it possible to use them in online and interactive applications.

The package can be easily interfaced with standard libraries for robotic manipulator rigid body simulation such as robotic-toolbox or pinocchio, as well as human musculoskeletal model biomechanics softwares opensim and biorbd. The package can also be used with the Robot Operating System (ROS).

The package additionally implements a set of visualization tools for polytopes and ellipsoids based on the Python package matplotlib intended for fast prototyping and quick and interactive visualization.

See full API documentation and docs.

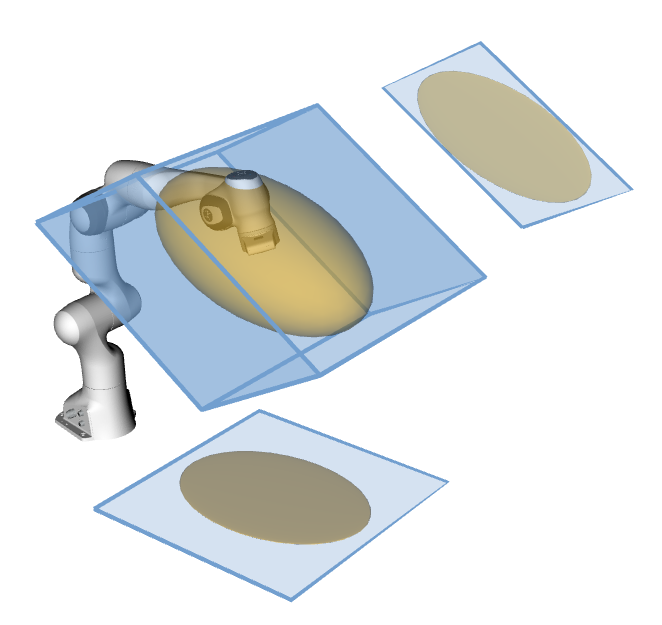
Robotic manipulator capacity metrics

For the robotic manipulators the package integrates several velocity, force and acceleration capacity calculation functions based on ellipsoids:

  • Velocity (manipulability) ellipsoid
    E_vel = {dx | dx = J.dq, ||dq||<1 }
  • Acceleration (dynamic manipulability) ellipsoid
    E_acc = {ddx | ddx = J.M^(-1).t, ||t||<1 }
  • Force ellipsoid
    E_for = {f | J^T.f = t, ||t||<1 }

And polytopes:

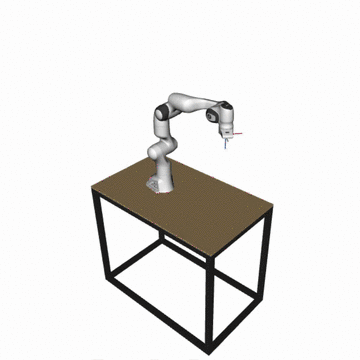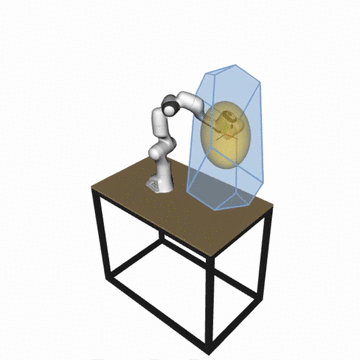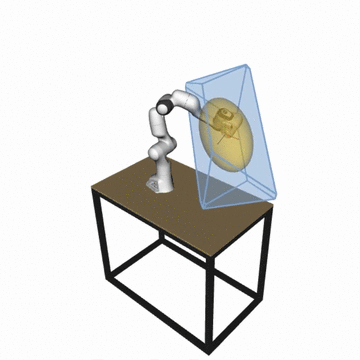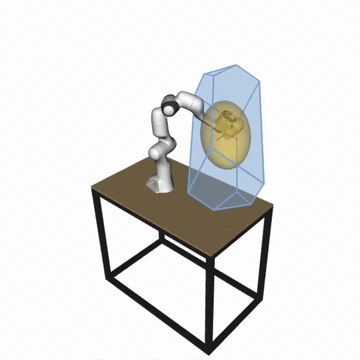
  • Velocity polytope
    P_vel = {dx | dx = J.dq, dq_min < dq < dq_max}
  • Acceleration polytope
    P_acc = {ddx | ddx = J.M^(-1).t, t_min < t < t_max}
  • Force polytope
    P_for = {f | J^T.f = t, t_min < t < t_max}
  • NEW 📢: Reachable space of the robot with the horizon T
    P_x = {x | x = JM(-1)tT^2/2, t_min < t < t_max, dq_min < M^(-1)tT < dq_max, q_min < M^(-1)tT^2/2 < q_max}
  • Force polytopes Minkowski sum and intersection

Where J is the robot jacobian matrix, f is the vector of cartesian forces,dx and ddx are vectors fo cartesian velocities and accretions, dq is the vector of the joint velocities and t is the vector of joint torques.

Reachable space polytope approximation is based on this paper:
Approximating robot reachable space using convex polytopes
by Skuric, Antun, Vincent Padois, and David Daney.
In: Human-Friendly Robotics 2022: HFR: 15th International Workshop on Human-Friendly Robotics. Cham: Springer International Publishing, 2023.

The force polytope functions have been implemented according to the paper:
On-line force capability evaluation based on efficient polytope vertex search
by A.Skuric, V.Padois and D.Daney
Published on ICRA2021

The force polytope functions have been implemented according to the paper:
On-line force capability evaluation based on efficient polytope vertex search
by A.Skuric, V.Padois and D.Daney
Published on ICRA2021

And the velocity and acceleration polytopes are resolved using the Hyper-plane shifting method:
Characterization of Parallel Manipulator Available Wrench Set Facets
by Gouttefarde M., Krut S.
In: Lenarcic J., Stanisic M. (eds) Advances in Robot Kinematics: Motion in Man and Machine. Springer, Dordrecht (2010)

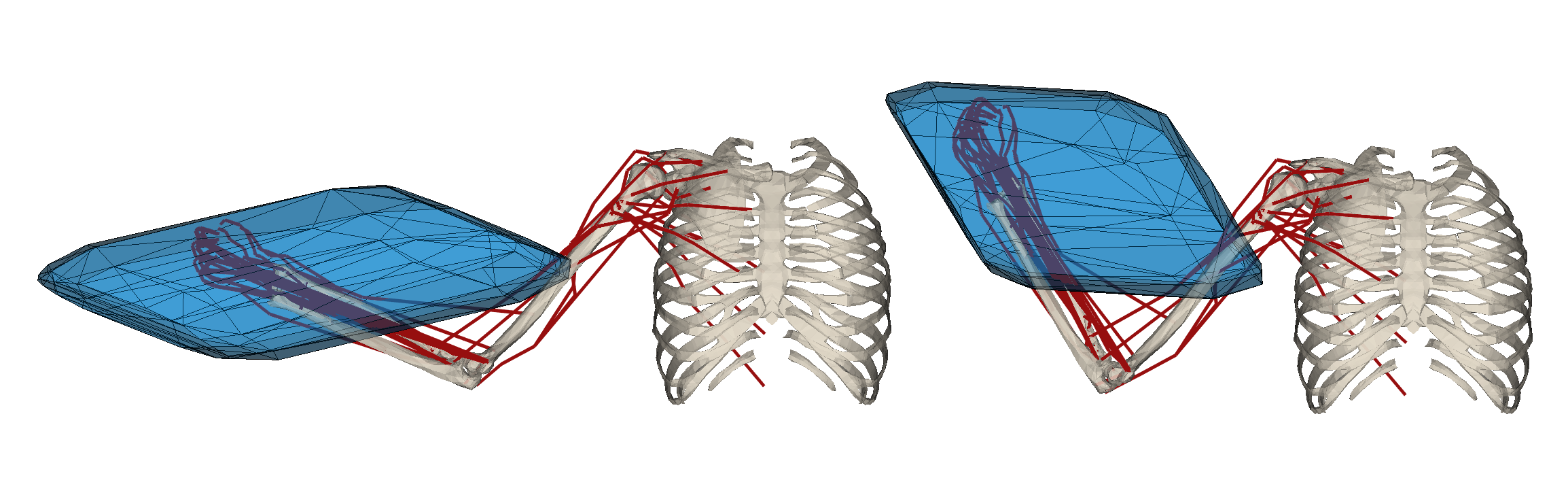
Human musculoskeletal models capacity metrics

For the human musculoskeletal models this package implements the ellipsoid and polytope evaluation functions. The implemented ellipsoids are:

  • Velocity (manipulability) ellipsoid
    E_vel = {dx | dx = J.dq, dl = L.dq, ||dl||<1 }
  • Acceleration (dynamic manipulability) ellipsoid
    E_acc = {ddx | ddx = J.M^(-1).N.F, ||F||<1 }
  • Force ellipsoid
    E_for = {f | J^T.f = N.F, ||F||<1 }

And polytopes:

  • Velocity polytope
    P_vel = {dx | dx = J.dq, dl = L.dq dl_min < dl < dl_max}
  • Acceleration polytope
    P_acc = {ddx | ddx = J.M^(-1).N.F, F_min < F < F_max}
  • Force polytope
    P_for = {f | J^T.f = N.F, F_min < F < F_max}

Where J is the model's jacobian matrix, L si the muscle length jacobian matrix, N= -L^T is the moment arm matrix, f is the vector of cartesian forces,dx and ddx are vectors fo cartesian velocities and accretions, dq is the vector of the joint velocities, t is the vector of joint torques, dl is the vector of the muscle stretching velocities and F is the vector of muscular forces.

The force and velocity polytope functions have been implemented according to the paper:
On-line feasible wrench polytope evaluation based on human musculoskeletal models: an iterative convex hull method
by A.Skuric, V.Padois, N.Rezzoug and D.Daney
Submitted to RAL & ICRA2022

And the acceleration polytopes are resolved using the Hyper-plane shifting method:
Characterization of Parallel Manipulator Available Wrench Set Facets
by Gouttefarde M., Krut S.
In: Lenarcic J., Stanisic M. (eds) Advances in Robot Kinematics: Motion in Man and Machine. Springer, Dordrecht (2010)

Polytope evaluation algorithms

There are three methods implemented in this paper to resolve all the polytope calculations:

  • Hyper-plane shifting method (HPSM)
  • Iterative convex hull method (ICHM)
  • Vertex enumeration algorithm (VEPOLI2)

All of the methods are implemented in the module pycapacity.algorithms and can be used as standalone functions. See in docs for more info.

Hyper-plane shifting method (HPSM)

Characterization of Parallel Manipulator Available Wrench Set Facets
by Gouttefarde M., Krut S.
In: Lenarcic J., Stanisic M. (eds) Advances in Robot Kinematics: Motion in Man and Machine. Springer, Dordrecht (2010)

This method finds the half-space representation of the polytope of a class:

P = {x | x = By, y_min <= y <= y_max }

To find the vertices of the polytope after finding the half-space representation Hx <= d an convex-hull algorithm is used.

The method is a part of the pycapacity.algorithms module hyper_plane_shift_method, See in docs for more info.

Iterative convex-hull method (ICHM)

On-line feasible wrench polytope evaluation based on human musculoskeletal models: an iterative convex hull method
by A.Skuric, V.Padois, N.Rezzoug and D.Daney
Submitted to RAL & ICRA2022

This method finds both vertex and half-space representation of the class of polytopes:

P = {x | Ax = By, y_min <= y <= y_max }

And it can be additionally extended to the case where there is an additional projection matrix P making a class of problems:

P = {x | x= Pz, Az = By, y_min <= y <= y_max }

The method is a part of the pycapacity.algorithms module iterative_convex_hull_method. See the docs for more info

Vertex enumeration algorithm (VEPOLI2)

On-line force capability evaluation based on efficient polytope vertex search
by A.Skuric, V.Padois and D.Daney
Published on ICRA2021

This method finds vertex representation of the class of polytopes:

P = {x | Ax = y, y_min <= y <= y_max }

To find the half-space representation (faces) of the polytope after finding the vertex representation an convex-hull algorithm is used.

The method is a part of the pycapacity.algorithms module vertex_enumeration_vepoli2. See the docs for more info

Installation

All you need to do to install it is:

pip install pycapacity

And include it to your python project

import pycapacity.robot 
# and/or
import pycapacity.human 
#and/or
import pycapacity.algorithms 
#and/or
import pycapacity.visual 
#and/or
import pycapacity.objects

Other way to install the code is by installing it directly from the git repo:

pip install git+https://github.com/auctus-team/pycapacity.git

Package API docs

See full docs at the link

Contributing and discussions

For all the questions regarding the potential implementation, applications, supported hardware and similar please don't hesitate to leave an issue or start a discussion

It is always helpful to hear the stories/problems/suggestions of people implementing the code!

Github Issues & Pull requests

Please do not hesitate to leave an issue if you have problems/advices/suggestions regarding the code!

If you'd like to contribute to this project but you are not very familiar with github, don't worry, let us know either by starting the discussion or posting a github issue.

Citing pycapacity in scientific publications

We are very happy that pycapacity has been used as a component of several research project and has made its way to several scientific papers. We are hoping that this trend is going to continue as the project matures and becomes more robust!

A short resume paper about pycapacity has been published in the Journal of Open Source Software:

pycapacity: a real-time task-space capacity calculation package for robotics and biomechanics
A. Skuric, V. Padois and D. Daney
Journal of Open Source Software, 8(89), 5670, https://doi.org/10.21105/joss.05670

If you are interested in citing pycapacity in your research, we suggest you to cite our paper:

@article{Skuric2023pycapacity,
    author = {Skuric, Antun and Padois, Vincent and Daney, David},
    doi = {10.21105/joss.05670},
    journal = {Journal of Open Source Software},
    month = sep,
    number = {89},
    pages = {5670},
    title = {{Pycapacity: a real-time task-space capacity calculation package for robotics and biomechanics}},
    url = {https://joss.theoj.org/papers/10.21105/joss.05670},
    volume = {8},
    year = {2023}
}

Code examples

See demo_notebook.ipynb for more examples of how ot use the module.

Randomised serial robot example

"""
A simple example program for 3d force polytope 
evaluation of a randomised 6dof robot 
"""
import pycapacity.robot as capacity # robot capacity module
import numpy as np

m = 3 # 3d forces
n = 6 # robot dof

J = np.array(np.random.rand(m,n)) # random jacobian matrix

t_max = np.ones(n)  # joint torque limits max and min
t_min = -np.ones(n)

f_poly = capacity.force_polytope(J,t_min, t_max) # calculate the polytope vertices and faces

print(f_poly.vertices) # display the vertices

# plotting the polytope
import matplotlib.pyplot as plt
from pycapacity.visual import * # pycapacity visualisation tools
fig = plt.figure(4)

# draw faces and vertices
plot_polytope(polytope=f_poly, plot=plt, label='force polytope', vertex_color='blue', edge_color='blue', alpha=0.2)

plt.legend()
plt.show()

Randomised muslucoskeletal model example

"""
A simple example program for 3d force polytope 
evaluation of a randomised 30 muscle 7dof 
human musculoskeletal model 
"""

import pycapacity.human as capacity # robot capacity module
import numpy as np

L = 30 # number of muscles
m = 3 # 3d forces
n = 6 # number of joints - dof

J = np.array(np.random.rand(m,n))*2-1 # random jacobian matrix
N = np.array(np.random.rand(n,L))*2-1 # random moment arm matrix

F_max = 100*np.ones(L)  # muscle forces limits max and min
F_min = np.zeros(L)

f_poly = capacity.force_polytope(J,N, F_min, F_max, 0.1) # calculate the polytope vertices and faces

print(f_poly.vertices) # display the vertices


# plotting the polytope
import matplotlib.pyplot as plt
from pycapacity.visual import * # pycapacity visualisation tools
fig = plt.figure(4)

# draw faces and vertices
plot_polytope(polytope=f_poly, plot=plt, label='force polytope', vertex_color='blue', edge_color='blue', alpha=0.2)

plt.legend()
plt.show()