Skip to content

Latest commit

 

History

History
552 lines (340 loc) · 24.1 KB

DS-AVL-Tree-Insertion.md

File metadata and controls

552 lines (340 loc) · 24.1 KB
Raw

【动画笔记】数据结构-AVL树的插入操作

⚠ 本笔记前置知识: 二叉搜索(排序)树及其插入操作。

本文主要围绕平衡因子、纸上做题思路、失衡类型(LL/RR/LR/RL)、失衡调整方法、插入后回溯这几部分知识点展开。

  • 注:

    1. 本笔记中的平衡二叉树规定所有左子树都小于其父节点，所有右子树都大于其父节点。

    2. 本笔记中的平衡因子计算方法是左子树高度 - 右子树高度。

目录

简单介绍一下下

AVL树又称二叉平衡搜索(排序)树，其最大的特点就是能维持所有节点的左右子树高度差绝对值不大于1。

因此，AVL树的插入操作要能维持住:

  1. 二叉搜索树的节点大小关系。

  2. 平衡二叉树中每个节点的【平衡因子】绝对值不大于1。

平衡因子

一般对于AVL树中的每个节点都会添加一个平衡因子(Balance Factor)字段，平衡因子的值就是左右子树的高度差，程序借此判断某棵子树是否平衡。

简述平衡二叉树的插入操作

AVL树的插入操作在二叉搜索(排序)树的插入的基础上新增了如下两个过程:

  1. 插入过程中将沿途比较的节点压入栈。

  2. 插入完成后，借助弹栈来沿着插入时比较的各节点回到整棵树的根节点 (从叶节点到根结点进行回溯):

    • 更新沿途各节点的高度。(通过高度计算平衡因子)

    • 沿途检查各节点的平衡因子，若出现了平衡因子绝对值 > 1的情况，则对不平衡的子树进行调整以保证整棵树的平衡性。

✨ 当然，这里的插入操作也是可以用递归来实现的。

✨ 如果AVL树节点中有指向父节点的指针变量，那么这个过程就不需要栈辅助了，直接向上遍历【插入节点】的所有祖先节点直至回到根节点即可。

什么是失衡节点

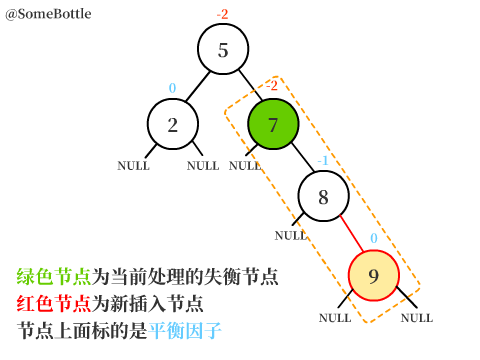
当树中某个节点的平衡因子 $BF \notin \left [ -1,1 \right ]$ 时，这个节点就是失衡节点。

以这个失衡节点为根节点的子树就是一棵不平衡的子树。

纸上快速做题思路

这一招适合纸上解题，可以结合程序实现一起理解。
另外，字丑勿cue（╥﹏╥）

首先插入新节点（红色的节点就是新插入的节点）:

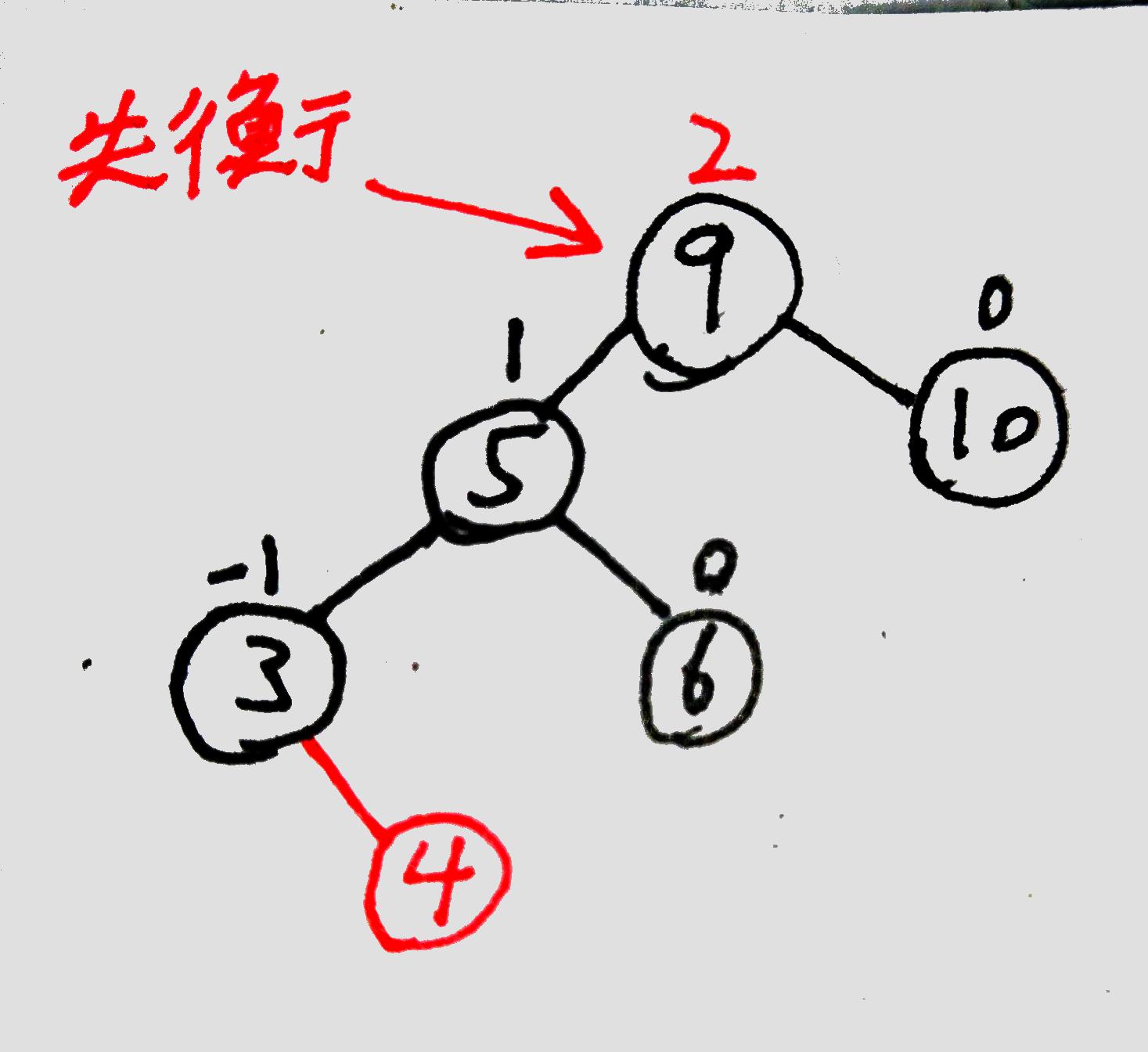
此时【值为9的节点】平衡因子为2，为失衡节点。

  1. 从失衡节点开始，沿着【刚刚插入新节点的比较路径】找，找到其中与其最邻近的两个点:

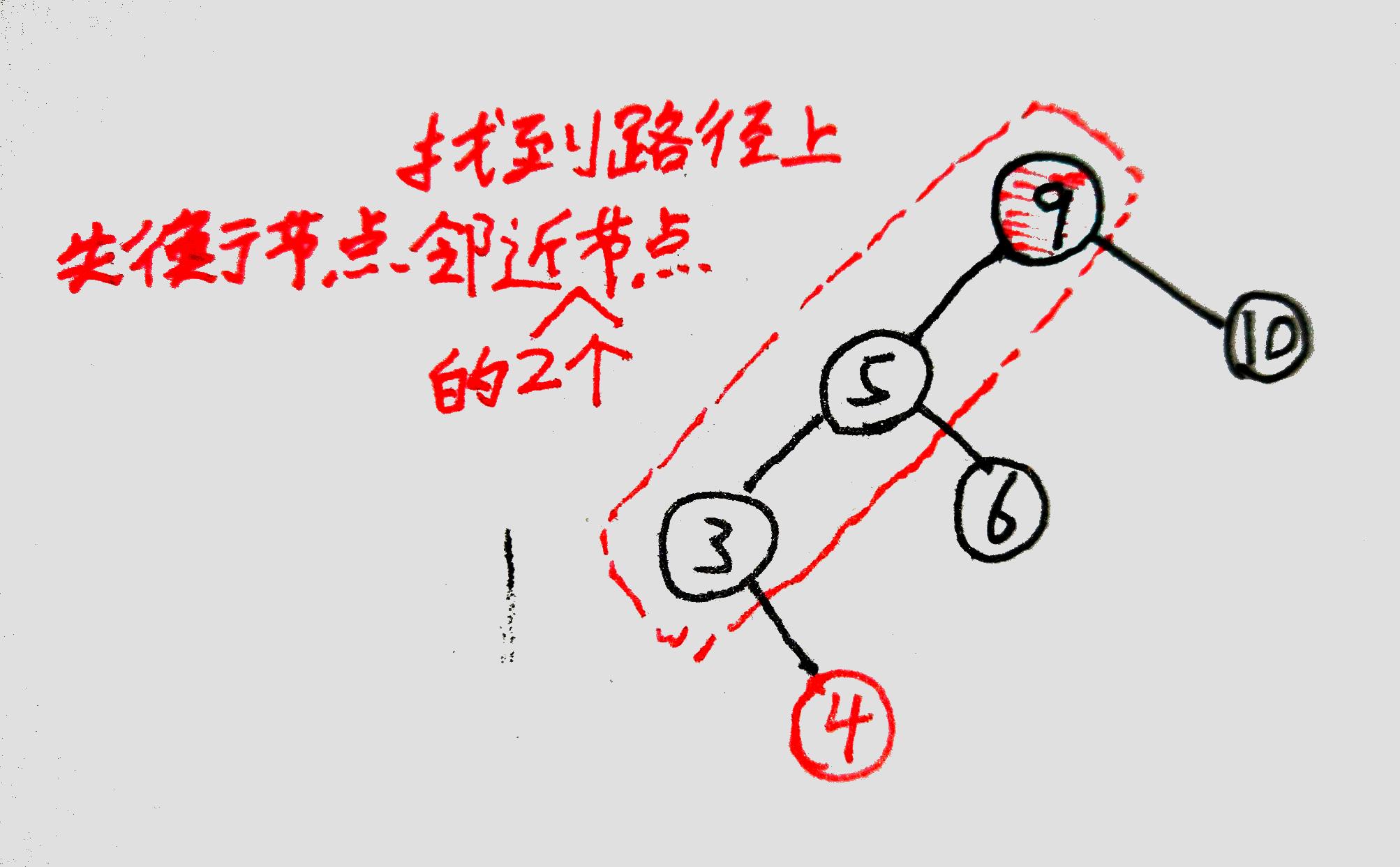
    （插入④时的比较路径是⑨->⑤->③，因此图中就找到了③、⑤、⑨）

  2. 包括失衡节点在内，现在一共有三个节点，从中选择值的大小在中间的节点。（图中是⑤）

  3. 将除了中间值节点外的两个节点按照二叉搜索树的规则接到【中间值节点】上，然后将【中间值节点】接到原本失衡节点所在的位置，作为这棵子树的根节点。

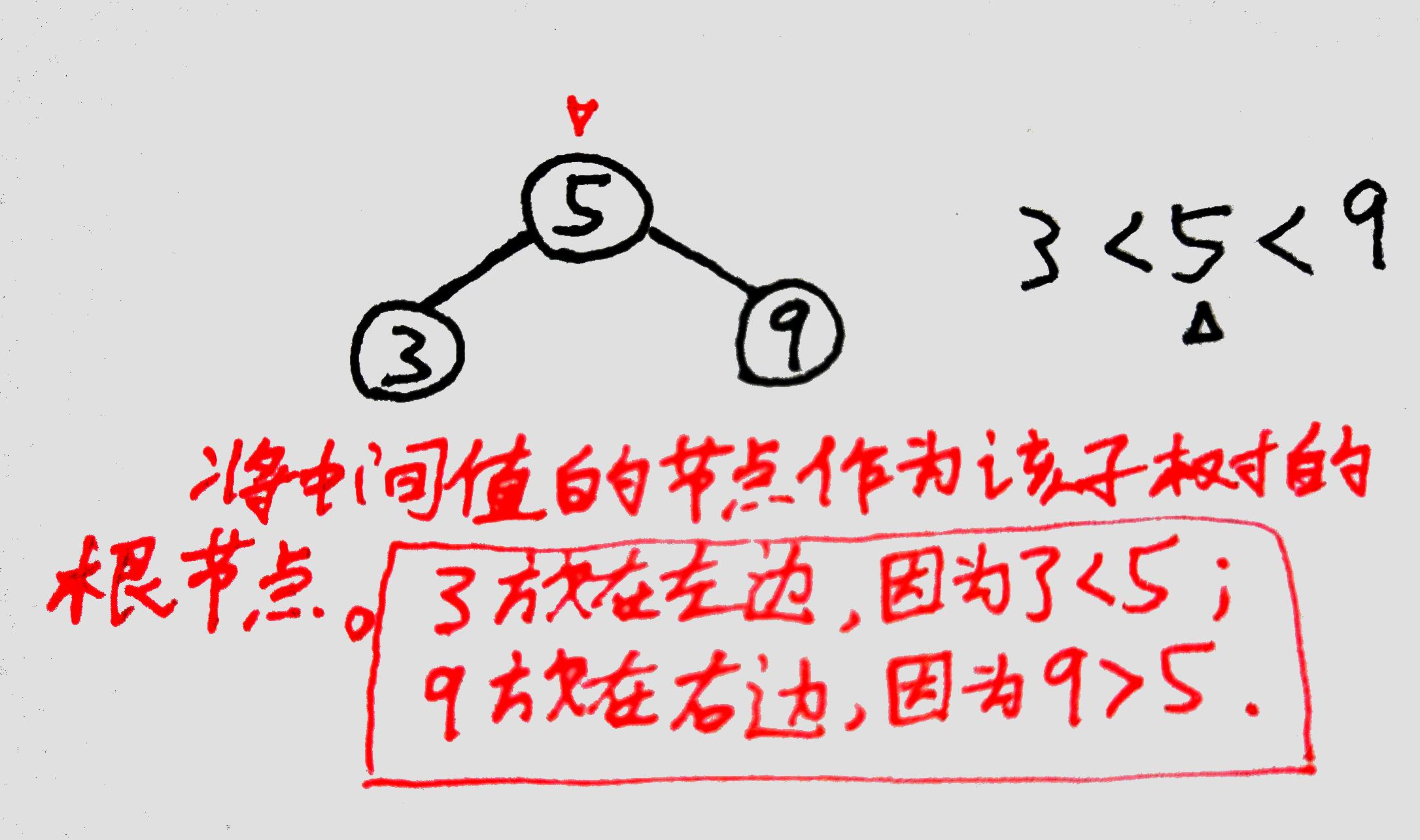
    （图中⑤替换了原本⑨的位置，③和⑨变成了⑤的孩子）

  4. 将【除了这三个节点之外】的节点按照二叉搜索树插入规则插入到这三个节点组成的子树中:

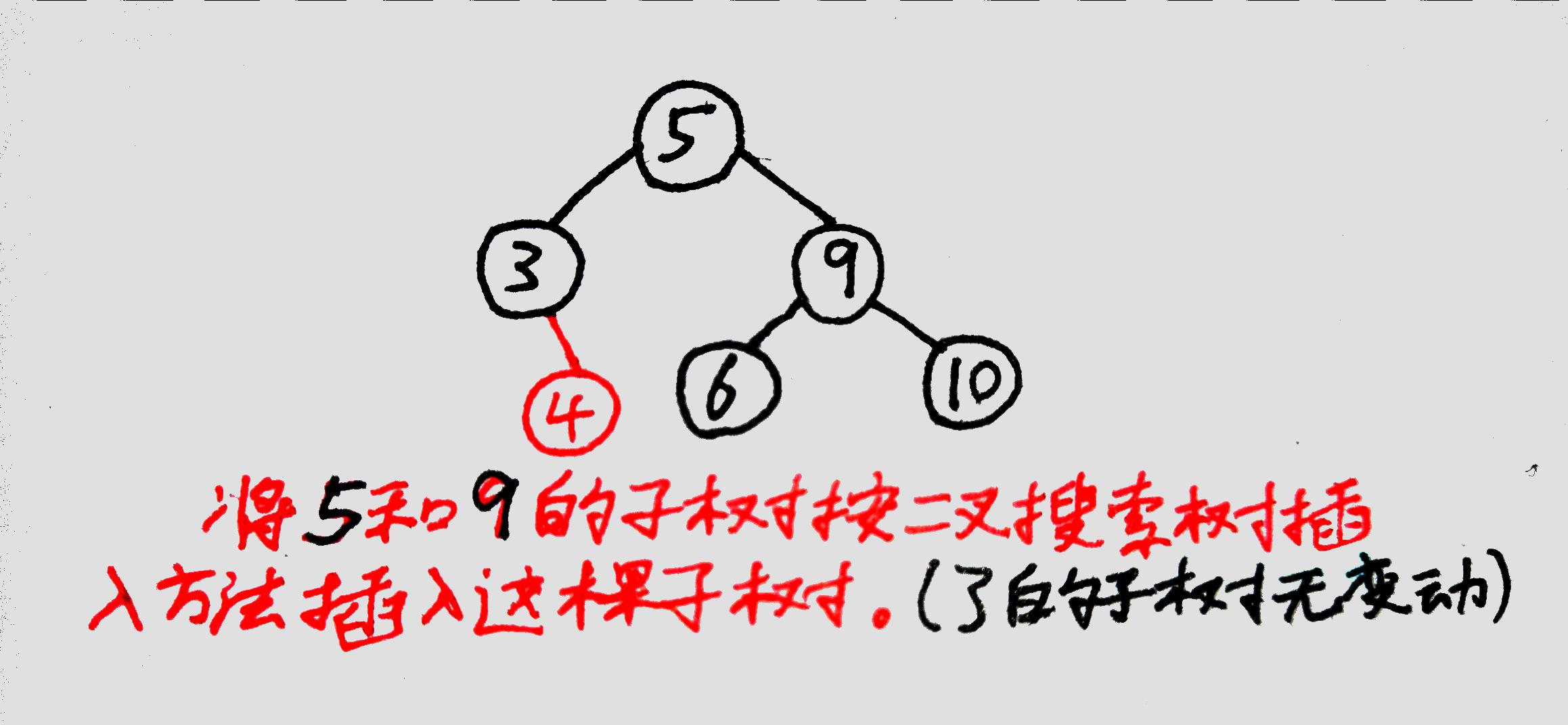
    （图中就是把剩余的节点④、⑥、⑩按规则插入到⑤为根的子树中，实际上④没有移动）

  5. 更新各节点的平衡因子:

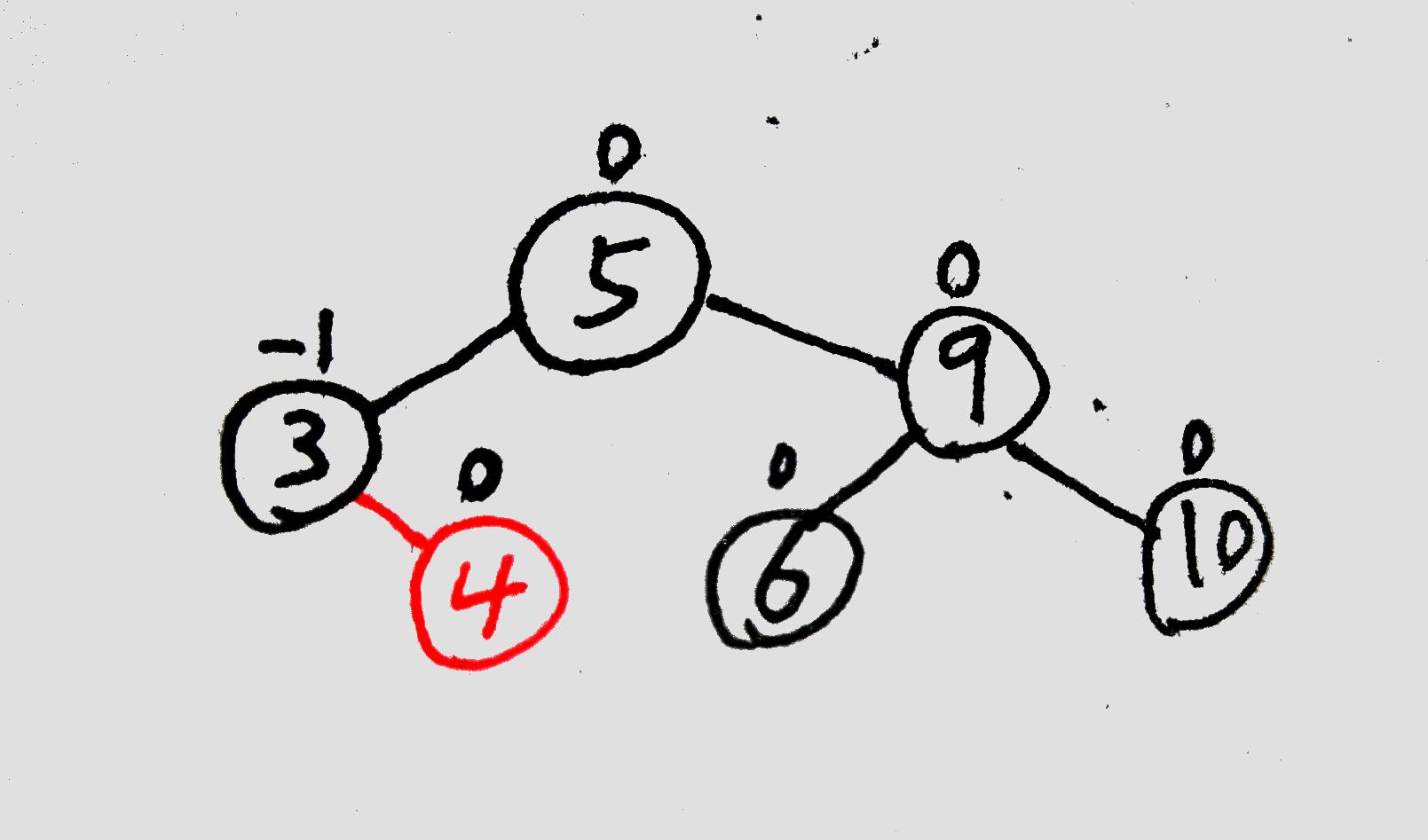
这种解题方法在纸上可以快速解决LL/LR/RL/RR这些类型的平衡调整问题，非常实用。

程序实现的话也可以靠这个思路来记忆和理解。

程序中定义树节点

程序实现没有标准答案，合理即可。

这里的树节点没有指向父节点的指针，因此往树中插入节点的过程中需要压栈，以在插入完成后进行回溯。

typedef struct TreeNode *Tree;

struct TreeNode
{
    Tree left;  // 左子树
    Tree right; // 右子树
    int height; // 节点所在高度，平衡因子靠这个算
    int val;    // 节点值
};

失衡类型 - LL型失衡

LL型字面展开来看就是Left - Left。意思是新插入节点位于失衡节点的左孩子的左子树中。

举例

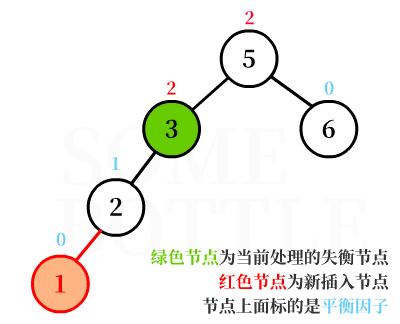
Unbalanced-LL-altered-2023-01-10

新节点插入在【值为2的节点】的左子树中，而【值为2的节点】又是【值为3的节点】的左孩子。

此时【值为3的节点】的平衡因子BF = 2-0 = 2 > 1，是一个失衡节点。

  • 注: 插入节点后的回溯过程当然是自下而上的，因此这里指的是自下而上首个失衡节点。

可以发现新节点插在【失衡节点】的左孩子的左子树中，这就是LL型失衡。

调整方法-右旋转

这里我结合纸上快速做题思路来写一下。

Unbalanced-LL-highlight-2023-01-10

【值为3的节点】是失衡节点。

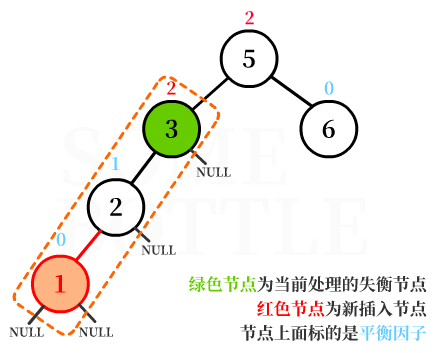
  1. 找到失衡节点沿着插入路径上的最邻近的两个节点，一共有三个节点。
    这里可以看成是以失衡节点为根结点的子树。

    • 就是图中框出来的几个节点。

  2. 找到三个节点中【值在中间的节点】，接下来的“右旋转”过程以它为轴。

    • 上图中找出的就是【值为2的节点】。其实就是失衡节点的左孩子。

  3. 将失衡节点以【值在中间的节点】为轴进行右旋转(顺时针)，让【值在中间的节点】变成这棵子树的新的根结点。

    • 上图中的【值为3的节点】围绕【值为2的节点】进行右旋转，变成【值为2的节点】的右子树。

    • 【值为2的节点】原本的右子树变成【值为3的节点】的左子树。

    • 【值为2的节点】成为新的子树根结点。(详见动图)

  • 动图演示过程:

    Unbalanced-LL-animation-2023-01-10

    通过动图演示就能很直观地看到这个“右旋转”的过程。

    可以发现旋转节点围绕的“旋转轴”就是【三个节点中中间值的节点】

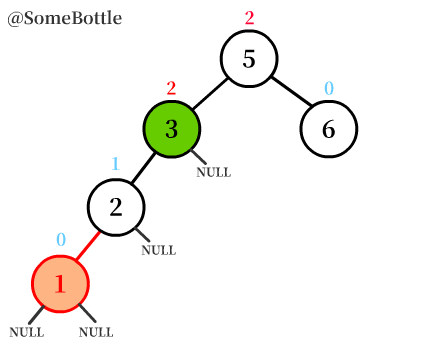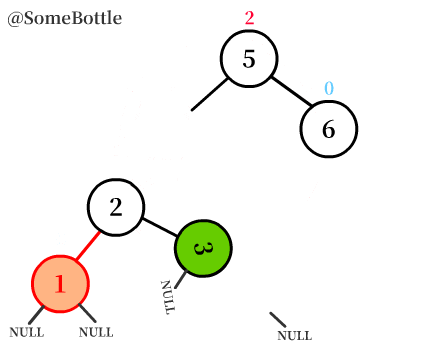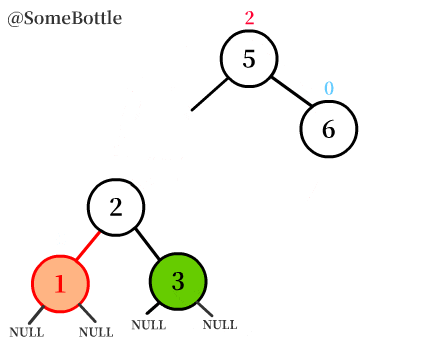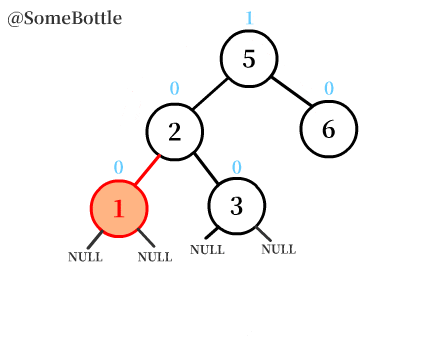
    图中我特意标出了空子树NULL，程序实现的时候一定要把子树考虑在内哦。

程序实现

程序实现的时候并不需要比较三个节点的大小。

对某个节点进行右旋转操作时，实际上就是把这个节点绕着其左孩子进行顺时针“旋转”。

// 失衡节点右旋操作，node是失衡结点
void rotateRight(Tree node)
{
    Tree nodeLeft = node->left;         // 失衡节点左子树
    Tree nodeRight = node->right;       // 失衡节点右子树
    Tree lChildLeft = nodeLeft->left;   // 失衡节点的左孩子的左子树
    Tree lChildRight = nodeLeft->right; // 失衡节点左孩子的右子树
    // 这里【没有指向父节点】的指针，我们直接修改结点的值来模拟移动结点即可
    int nodeVal = node->val;   // 失衡节点的值
    node->val = nodeLeft->val; // 交换失衡节点和左孩子的值
    nodeLeft->val = nodeVal;
    // 这里已经不是左孩子了，而是“旋转”下来的失衡节点
    nodeLeft->left = lChildRight; // 修改结点的左右子树
    nodeLeft->right = node->right;
    node->left = lChildLeft; // 和子树的根结点接上
    node->right = nodeLeft;
    // 此时node是子树根结点，lChildLeft是左子树，nodeLeft是右子树
    updateHeight(nodeLeft); // 更新有变动的结点的高度，先更新子树再更新根
    updateHeight(node);
}

失衡类型 - RR型失衡

RR型字面展开来看就是Right - Right。意思是新插入节点位于失衡节点的右孩子的右子树中。

举例

Unbalanced-RR-2023-02-03

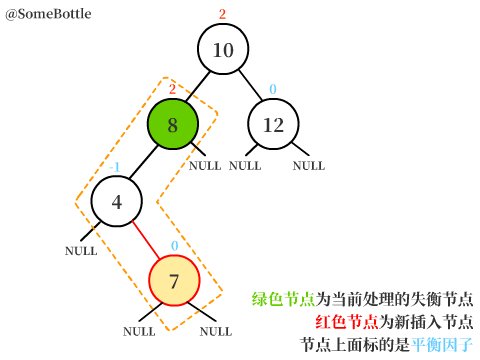
新节点插入在【值为8的节点】的右子树中，而【值为8的节点】又是【值为7的节点】的右孩子。

此时【值为7的节点】的平衡因子BF = 0-2 = -2 < -1，是一个失衡节点。

可以发现新节点插在【失衡节点】的右孩子的右子树中，这就是RR型失衡。

调整方法-左旋转

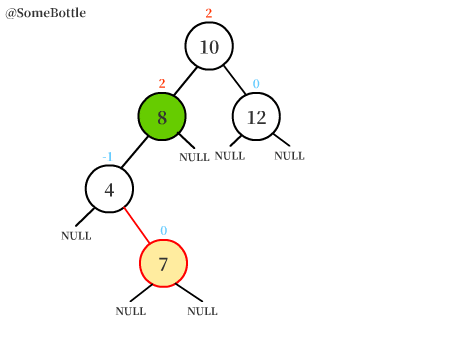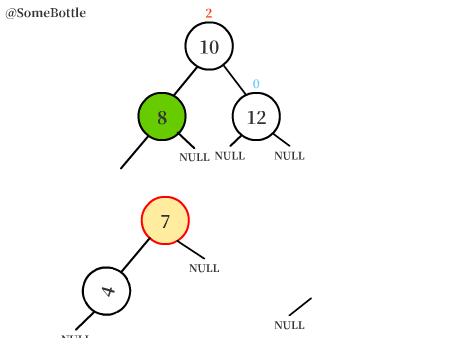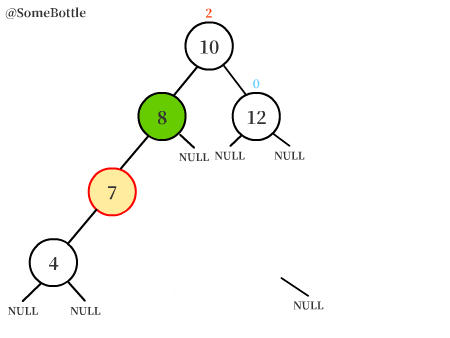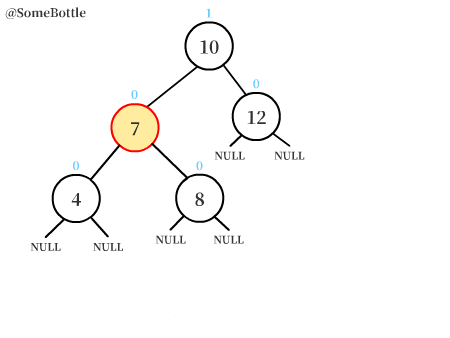
【值为7的节点】是失衡节点。

  1. 找到失衡节点沿着插入路径上的最邻近的两个节点，一共有三个节点。
    这里可以看成是以失衡节点为根结点的子树。

    • 就是图中框出来的几个节点。

  2. 找到三个节点中【值在中间的节点】，接下来的“左旋转”过程以它为轴。

    • 上图中找出的就是【值为8的节点】。其实就是失衡节点的右孩子。

  3. 将失衡节点以【值在中间的节点】为轴进行左旋转(逆时针)，让【值在中间的节点】变成这棵子树的新的根结点。

    • 上图中的【值为7的节点】围绕【值为8的节点】进行左旋转，变成【值为8的节点】的左子树。

    • 【值为8的节点】原本的左子树变成【值为7的节点】的右子树。

    • 【值为8的节点】成为新的子树根结点。(详见动图)

  • 动图演示过程:

    Unbalanced-RR-animation-2023-02-08

    RR型和LL型的调节过程中的操作是对称的。

程序实现

程序实现的时候并不需要比较三个节点的大小。

对某个节点进行左旋转操作时，实际上就是把这个节点绕着其右孩子进行逆时针“旋转”。

// 失衡节点左旋操作，node是失衡节点
void rotateLeft(Tree node)
{
    Tree nodeLeft = node->left;          // 失衡节点左子树
    Tree nodeRight = node->right;        // 失衡节点右子树
    Tree rChildLeft = nodeRight->left;   // 失衡节点的右孩子的左子树
    Tree rChildRight = nodeRight->right; // 失衡节点的右孩子的右子树
    // 这里【没有指向父节点】的指针，我们直接修改结点的值来模拟移动结点
    int nodeVal = node->val;
    node->val = nodeRight->val; // 交换失衡节点和右孩子的值
    nodeRight->val = nodeVal;
    // 这里的nodeRight就是“旋转”下来的节点
    nodeRight->right = rChildLeft;
    nodeRight->left = node->left;
    node->left = nodeRight;
    node->right = rChildRight;
    // 此时node是子树根结点，nodeRight是左子树，rChildRight是右子树
    updateHeight(nodeRight); // 更新有变动的结点的高度，先更新子树再更新根
    updateHeight(node);
}

失衡类型 - LR型失衡

LR型字面展开来看就是Left - Right。意思是新插入节点位于失衡节点的左孩子的右子树中。

举例

Unbalanced-LR-2023-02-09

新节点插入在【值为4的节点】的右子树中，而【值为4的节点】又是【值为8的节点】的左孩子。

此时【值为8的节点】的平衡因子BF = 2-0 = 2 > 1，是一个失衡节点。

可以发现新节点插在【失衡节点】的左孩子的右子树中，这就是LR型失衡。

调整方法-先左旋转再右旋转

【值为8的节点】是失衡节点。

  1. 找到失衡节点沿着插入路径上的最邻近的两个节点，一共有三个节点。
    这里可以看成是以失衡节点为根结点的子树。

    • 就是图中框出来的几个节点。

  2. 找到三个节点中【值在中间的节点】，接下来的“左旋转”过程以它为轴。

    • 上图中找出的就是【值为7的节点】。其实是失衡节点的左孩子的右孩子。

  3. 将【(三个节点中)值最小的节点】以【值在中间的节点】为轴进行左旋转(逆时针)，让【值在中间的节点】转上来，转变成LL型失衡的情况。

    • 上图中的【值为4的节点】围绕【值为7的节点】进行左旋转，变成【值为7的节点】的左子树。

    • 【值为7的节点】原本的左子树变成【值为4的节点】的右子树。

    • 【值为7的节点】成为了【值为8的节点】的左孩子。

  4. 此时整棵树已经调整成了LL型失衡的情况，接着用右旋转进行调整即可。详见动图。

  • 动图演示过程:

    Unbalanced-LR-animation-fixed-2023-02-09

    可以很直观地看到，首先用左旋转将平衡树转变为了LL失衡的情况，再用右旋转对树进行调整。

    可以发现整个过程中，旋转节点围绕的“旋转轴”都是【三个节点中中间值的节点】

程序实现

程序实现的时候并不需要比较三个节点的大小。

对某个节点A进行左旋转+右旋转操作时，实际上做的是:

  1. 令该节点A的左孩子为B，首先将B绕着B的右孩子进行逆时针旋转。
    (对B进行左旋转)

  2. 然后将节点A绕着B进行顺时针旋转。
    (对A进行右旋转)

// 失衡节点左右旋操作，node是失衡节点
rotateLeft(node->left); // 先对失衡节点的左孩子进行左旋
rotateRight(node);      // 再对失衡节点进行右旋

失衡类型 - RL型失衡

RL型字面展开来看就是Right - Left。意思是新插入节点位于失衡节点的右孩子的左子树中。

举例

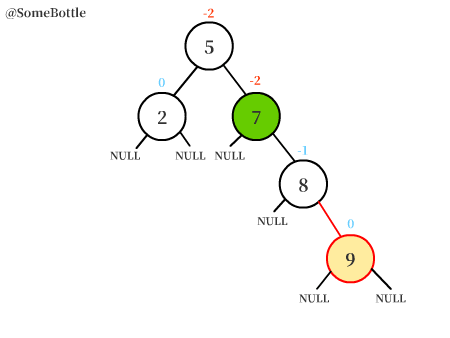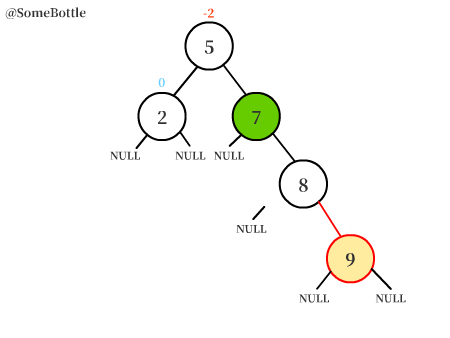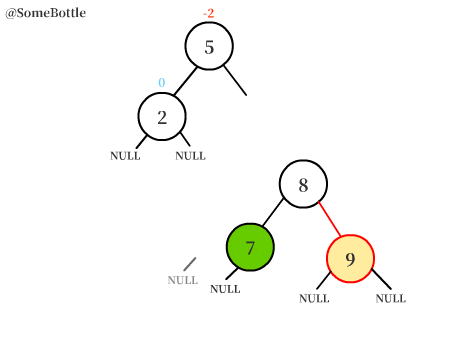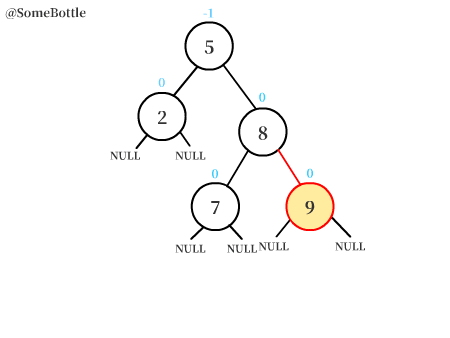
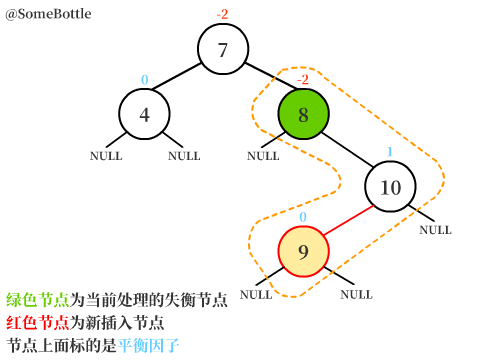
Unbalanced-RL-2023-02-10

新节点插入在【值为10的节点】的左子树中，而【值为10的节点】又是【值为8的节点】的右孩子。

此时【值为8的节点】的平衡因子BF = 0-2 = -2 < -1，是一个失衡节点。

可以发现新节点插在【失衡节点】的右孩子的左子树中，这就是RL型失衡。

调整方法-先右旋转再左旋转

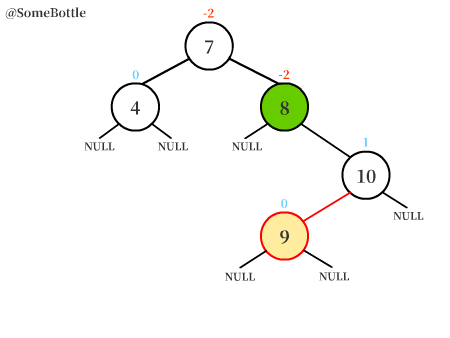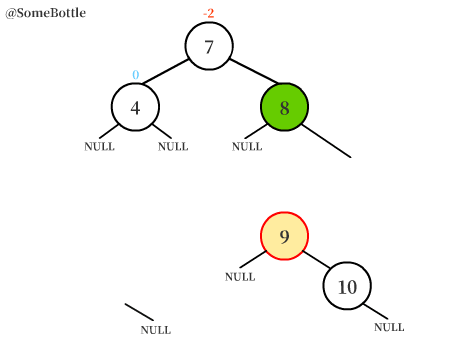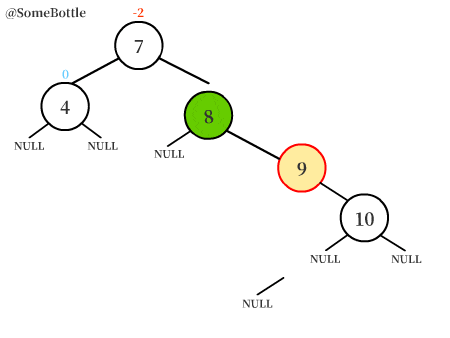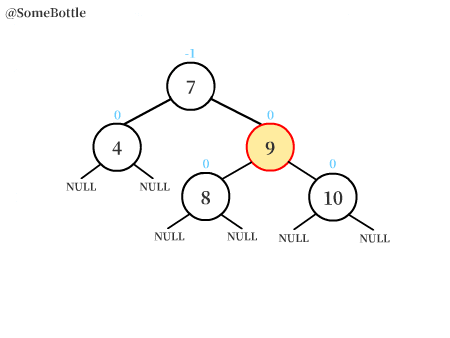
【值为8的节点】是失衡节点。

  1. 找到失衡节点沿着插入路径上的最邻近的两个节点，一共有三个节点。
    这里可以看成是以失衡节点为根结点的子树。

    • 就是图中框出来的几个节点。

  2. 找到三个节点中【值在中间的节点】，接下来的“右旋转”过程以它为轴。

    • 上图中找出的就是【值为9的节点】。其实是失衡节点的右孩子的左孩子。

  3. 将【(三个节点中)值最大的节点】以【值在中间的节点】为轴进行右旋转(顺时针)，让【值在中间的节点】转上来，转变成RR型失衡的情况。

    • 上图中的【值为10的节点】围绕【值为9的节点】进行右旋转，变成【值为9的节点】的右子树。

    • 【值为9的节点】原本的右子树变成【值为10的节点】的左子树。

    • 【值为9的节点】成为了【值为8的节点】的右孩子。

  4. 此时整棵树已经调整成了RR型失衡的情况，接着用左旋转进行调整即可。详见动图。

  • 动图演示过程:

    Unbalanced-RL-animation-2023-02-10

    可以很直观地看到，首先用右旋转将平衡树转变为了RR失衡的情况，再用左旋转对树进行调整。

    LR型和RL型的调节过程中的操作也是对称的。

    可以发现整个过程中，旋转节点围绕的“旋转轴”始终都是【三个节点中中间值的节点】

程序实现

程序实现的时候并不需要比较三个节点的大小。

对某个节点A进行右旋转+左旋转操作时，实际上做的是:

  1. 令该节点A的右孩子为B，首先将B绕着B的左孩子进行顺时针旋转。 (对B进行右旋转)

  2. 然后将节点A绕着B进行逆时针旋转。 (对A进行左旋转)

// 失衡节点右左旋操作，node是失衡节点
rotateRight(node->right); // 先对失衡节点的右孩子进行右旋
rotateLeft(node);         // 再对失衡节点进行左旋

程序中判断失衡类型

程序中，咱们依赖于平衡因子来判断失衡类型。

平衡因子由左右子树的高度差决定，因此根据平衡因子能判断出新节点插入在哪里:

  • 当失衡节点的平衡因子 > 1 时:

    • 如果失衡节点的左孩子的平衡因子 > 0，则是LL型失衡。

    • 如果失衡节点的左孩子的平衡因子 < 0，则是LR型失衡。

  • 当失衡节点的平衡因子 < -1 时:

    • 如果失衡节点的右孩子的平衡因子 < 0，则是RR型失衡。

    • 如果失衡节点的右孩子的平衡因子 > 0，则是RL型失衡。

展开查看程序实现 
// curr节点失衡了, 需要进行调整
// bf是这个节点的平衡因子
if (bf > 1) // 失衡节点的平衡因子>1，说明左子树比较高，因此找失衡节点的左孩子
{
    // 看失衡节点左孩子的平衡因子
    int leftBf = balanceFactor(curr->left);
    if (leftBf > 0) // 这个左孩子的左子树高于右子树
    {
        // 这说明是LL型，即插入在失衡节点【左孩子的左子树中】而导致失衡，需要进行“右旋”进行调整
        rotateRight(curr);
    }
    else // 这个左孩子的右子树高于左子树
    {
        // 这说明是LR型，插入在失衡结点【左孩子的右子树中】而导致失衡，需要进行“左旋再右旋”进行调整
        rotateLeft(curr->left); // 先对左孩子进行左旋
        rotateRight(curr);      // 再对失衡节点进行右旋
    }
}
else if (bf < -1) // 失衡节点的平衡因子<-1，说明右子树比较高，因此找失衡节点的右孩子
{
    int rightBf = balanceFactor(curr->right);
    if (rightBf < 0) // 右孩子的右子树高于左子树
    {
        // 这说明是RR型，即插入在失衡节点【右孩子的右子树中】，需要进行“左旋”进行调整
        rotateLeft(curr);
    }
    else // 右孩子的左子树高于右子树
    {
        // 这说明是RL型，即插入在失衡节点【右孩子的左子树中】，需要进行“右旋再左旋”进行调整
        rotateRight(curr->right); // 先对右孩子进行右旋
        rotateLeft(curr);         // 再对失衡节点进行左旋
    }
}

插入后一定要回溯到根节点吗？

本文开头咱简述了一下AVL树的插入操作。

在往AVL树中插入了一个节点后，需要沿着祖先节点向上回溯到根节点，沿途更新每个节点的高度，并寻找失衡的节点来进行调整。

节点的高度用于计算平衡因子。

遇到平衡因子为0的节点时回溯可以停止

💡 实际上，在插入后的回溯过程中，如果发现某节点的平衡因子 = 0，就可以不用再回溯了。

原因

究其原因，咱们得关注一下插入前和插入后的平衡因子变化情况:

  1. 插入前，AVL树中每棵子树都是平衡的，也就是说，所有节点的平衡因子都在[-1, 1]范围内。

  2. 若树中某节点A的平衡因子 $BF \in \left \lbrace -1,1 \right \rbrace$ ，就意味着节点A的左子树和右子树的高度差的绝对值为1。

    复习一下，BF = 左子树高度 - 右子树高度。

  3. 如果当插入了一个新节点后，节点A的平衡因子 $BF=0$ :

    插入前 插入后 子树的高度 节点A所在的高度
    节点A的平衡因子 $BF=1$ $BF=0$ 节点A的右子树变高，说明新节点插入在其右子树中 无变化
    节点A的平衡因子 $BF=-1$ $BF=0$ 节点A的左子树变高，说明新节点插入在其左子树中 无变化

  4. 【节点A所在的高度】取决于其较高的一棵子树，而当平衡因子BF从【1或-1】变为0时，只是节点A的【原本较矮的一棵子树】的高度变得和较高的子树高度一样了，因此节点A所在的高度理所当然没有发生改变。

  5. 在插入后的回溯过程中会更新沿途节点的高度。在更新节点A的父节点【FA】的高度时，由于节点A的高度没有发生变化，因此FA节点的高度也不会发生变化；同时，FA节点的平衡因子也不会发生变化。

    FA节点的高度 = max(节点A的高度, FA节点另一个孩子的高度) + 1

  6. 依此类推，节点A的所有祖先节点的高度和平衡因子都不会发生变化，因此回溯过程在节点A这里就可以停止了。

所以，在回溯过程中如果遇到了平衡因子为0的节点，就可以不用再继续下去了。

相关题目

正好在DotCpp上找到了一个只考察AVL树插入和查找的题目:

我的题解:

谢谢

感谢你看到这里。希望我的笔记能对你有所帮助~ 再会！( ´･ω･)ﾉ