Copyright © 2005-2017 Carl Youngblood carl@youngbloods.org
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
SBN makes it easy to use Bayesian Networks in your ruby application. Why would you want to do this? Bayesian networks are excellent tools for making intelligent decisions based on collected data. They are used to measure and predict the probabilities of various outcomes in a problem space.
A Bayesian Network is a directed acyclic graph representing the variables in a problem space, the causal relationships between these variables and the probabilities of these variables’ possible states, as well as the algorithms used for inference on these variables.
Installation of SBN is simple:
# gem install sbn
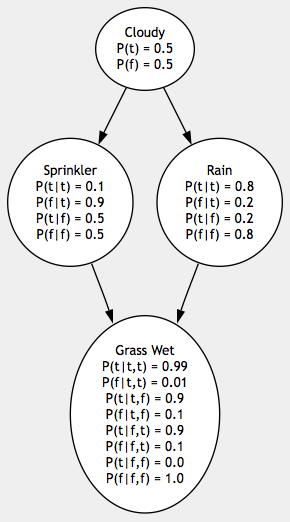
We’ll begin with a network whose probabilities have been pre-determined. This example comes from the excellent Artificial Intelligence: A Modern Approach, by Russell & Norvig. Later we’ll see how to determine a network’s probabilities from sample points. Our sample network has four variables, each of which has two possible states:
-
Cloudy: :true if sky is cloudy, :false if sky is sunny.
-
Sprinkler: :true if sprinkler was turned on, :false if not. Whether or not it’s cloudy has a direct influence on whether or not the sprinkler is turned on, so there is a parent-child relationship between Sprinkler and Cloudy.
-
Rain: :true if it rained, :false if not. Whether or not it’s cloudy has a direct influence on whether or not it will rain, so there is a relationship there too.
-
Grass Wet: :true if the grass is wet, :false if not. The state of the grass is directly influenced by both rain and the sprinkler, but cloudiness has no direct influence on the state of the grass, so grass has a relationship with both Sprinkler and Rain but not Cloudy.
Each variable holds a state table representing the conditional probabilties of each of its own states given each of its parents’ states. Cloudy has no parents, so it only has probabilities for its own two states. Sprinkler and Rain each have one parent, so they must specify probabilities for all four possible combinations of their own states and their parents’ states. Since Grass Wet has two parents, it must specify all eight possible combinations of states. Since we live in a logical universe, each variable’s possible states given a specific combination of its parents’ states must add up to 1.0. Notice that Cloudy’s probabilities add up to 1.0, Sprinkler’s states given Cloudy == :true add up to 1.0 and so on.
In the following code, the network shown above is created and its variables are initialized and connected to one another. The “evidence” is then set. This evidence represents observations of variables in the problem state. In this case, the Sprinkler variable was observed to be in the :false state, and the Rain variable was observed to be in the :true state. Setting this evidence in the network is analogous to knowing more about the problem space. With more knowledge of the problem space, the posterior probabilities of the remaining unobserved variables can be predicted with greater accuracy. After setting the evidence, query_variable() is called on the Grass Wet variable. This returns a hash of possible states and their posterior probabilties.
require 'rubygems'
require 'sbn'
net = Sbn::Net.new("Grass Wetness Belief Net")
cloudy = Sbn::Variable.new(net, :cloudy, [0.5, 0.5])
sprinkler = Sbn::Variable.new(net, :sprinkler, [0.1, 0.9, 0.5, 0.5])
rain = Sbn::Variable.new(net, :rain, [0.8, 0.2, 0.2, 0.8])
grass_wet = Sbn::Variable.new(net, :grass_wet, [0.99, 0.01, 0.9, 0.1, 0.9, 0.1, 0.0, 1.0])
cloudy.add_child(sprinkler) # also creates parent relationship
cloudy.add_child(rain)
sprinkler.add_child(grass_wet)
rain.add_child(grass_wet)
evidence = {:sprinkler => :false, :rain => :true}
net.set_evidence(evidence)
net.query_variable(:grass_wet)
=> {:true=>0.8995, :false=>0.1005} # inferred probabilities for grass_wet
# given sprinkler == :false and rain == :true
The order that probabilities are supplied is as follows. Always alternate between the states of the variable whose probabilities you are supplying. Supply the probabilities of these states given the variable’s parents in the order the parents were added, from right to left, with the rightmost (most recently added) parent alternating first. For example, if I have one variable A with two parents B and C, A having three states, B having two, and C having four, I would supply the probabilities in the following order:
P(A1|B1,C1) # this notation means "The probability of A1 given B1 and C1" P(A2|B1,C1) P(A3|B1,C1) P(A1|B1,C2) P(A2|B1,C2) P(A3|B1,C2) P(A1|B1,C3) P(A2|B1,C3) P(A3|B1,C3) P(A1|B1,C4) P(A2|B1,C4) P(A3|B1,C4) P(A1|B2,C1) P(A2|B2,C1) P(A3|B2,C1) P(A1|B2,C2) P(A2|B2,C2) P(A3|B2,C2) P(A1|B2,C3) P(A2|B2,C3) P(A3|B2,C3) P(A1|B2,C4) P(A2|B2,C4) P(A3|B2,C4)
A more verbose, but possibly less confusing way of specifying probabilities is to set the specific probability for each state separately using a hash to represent the combination of states:
net = Sbn::Net.new("Grass Wetness Belief Net") cloudy = Sbn::Variable.new(net, :cloudy) # states default to :true and :false sprinkler = Sbn::Variable.new(net, :sprinkler) rain = Sbn::Variable.new(net, :rain) grass_wet = Sbn::Variable.new(net, :grass_wet) cloudy.add_child(sprinkler) cloudy.add_child(rain) sprinkler.add_child(grass_wet) rain.add_child(grass_wet) cloudy.set_probability(0.5, {:cloudy => :true}) cloudy.set_probability(0.5, {:cloudy => :false}) sprinkler.set_probability(0.1, {:sprinkler => :true, :cloudy => :true}) sprinkler.set_probability(0.9, {:sprinkler => :false, :cloudy => :true}) sprinkler.set_probability(0.5, {:sprinkler => :true, :cloudy => :false}) sprinkler.set_probability(0.5, {:sprinkler => :false, :cloudy => :false}) # etc etc
After your network is set up, you can set evidence for specific variables that you have observed and then query unknown variables to see the posterior probability of their various states. Given these inferred probabilties, one common decision-making strategy is to assume that the variables are set to their most probable states.
evidence = {:sprinkler => :false, :rain => :true}
net.set_evidence(evidence)
net.query_variable(:grass_wet)
=> {:true=>0.8995, :false=>0.1005} # inferred probabilities for grass_wet
# given sprinkler == :false and rain == :true
The only currently supported inference algorithm is the Markov Chain Monte Carlo (MCMC) algorithm. This is an approximation algorithm. Given the complexity of inference in Bayesian networks (NP-hard), exact inference is often intractable. The MCMC algorithm approximates the posterior probability for each variable’s state by generating a random set of states for the unset variables in proportion to each state’s posterior probability. It generates successive random states conditioned on the previous values of the non-evidence variables. The reason this works is because over time, the amount of time spent in each random state is proportional to its posterior probabilty.
Although it is sometimes useful to be able to specify a variable’s probabilities in advance, we usually begin with a clean slate, and only are able to make a reasonable estimate of each variable’s probabilities after collecting sufficient data. This process is easy with SBN. The parameter learning process requires complete sample points for all variables in the network. Each set of sample points is a hash with keys matching each variable’s name and values corresponding to each variable’s observed state. The more sample points you supply to your network, the more accurate its probability estimates will be.
net.learn([ {:cloudy => :true, :sprinkler => :false, :rain => :true, :grass_wet => :true}, {:cloudy => :true, :sprinkler => :true, :rain => :false, :grass_wet => :true}, {:cloudy => :false, :sprinkler => :false, :rain => :true, :grass_wet => :true}, {:cloudy => :true, :sprinkler => :false, :rain => :true, :grass_wet => :true}, {:cloudy => :false, :sprinkler => :true, :rain => :false, :grass_wet => :false}, {:cloudy => :false, :sprinkler => :false, :rain => :false, :grass_wet => :false}, {:cloudy => :false, :sprinkler => :false, :rain => :false, :grass_wet => :false}, {:cloudy => :true, :sprinkler => :false, :rain => :true, :grass_wet => :true}, {:cloudy => :true, :sprinkler => :false, :rain => :false, :grass_wet => :false}, {:cloudy => :false, :sprinkler => :false, :rain => :false, :grass_wet => :false}, ])
Sample points can also be specified one set at a time and calculation of the probability tables can be deferred until a specific time:
net.add_sample_point({:cloudy => :true, :sprinkler => :false, :rain => :true, :grass_wet => :true}) net.add_sample_point({:cloudy => :true, :sprinkler => :true, :rain => :false, :grass_wet => :true}) net.set_probabilities_from_sample_points!
Networks store the sample points you have given them, so that future learning continues to take previous samples into account. The learning process is fairly simple. The frequency of each state combination in each variable is determined, and the number of occurrences for each state combination are divided by the total number of combinations learned on.
SBN currently supports the XMLBIF format for serializing Bayesian networks:
FILENAME = 'grass_wetness.xml' File.open(FILENAME, 'w') {|f| f.write(net.to_xmlbif) } reconstituted_net = net.from_xmlbif(File.read(FILENAME))
At present, sample points are not saved with your network, but this feature is anticipated in a future release.
Among SBN’s most powerful features are its advanced variable types, which make it much more convenient to handle real-world data and increase the relevancy of your results.
Sbn::StringVariable is used for handling string data. Rather than set a StringVariable’s states manually, rely on the learning process. During learning, you should pass the observed string for this variable for each sample point. Each observed string is divided into a series of n-grams (short character sequences) matching snippets of the observed string. A new variable is created (of class Sbn::StringCovariable) for each ngram, whose state will be :true or :false depending on whether the snippet is observed or not. These covariables are managed by the main StringVariable to which they belong and are transparent to you, the developer. They inherit the same parents and children as their managing StringVariable. By dividing observed string data into fine-grained substrings and determining separate probabilities for each substring occurrence, an extremely accurate understanding of the data can be developed.
Sbn::NumericVariable is used for handling numeric data, which is continuous and is thus more difficult to categorize than discrete states. Due to the nature of the MCMC algorithm used for inference, every variable in the network must have discrete states, but this limitation can be ameliorated by dynamically altering a numeric variable’s states according to the variance of the numeric data. Whenever learning occurs, the average and standard deviation of the observations for the NumericVariable are calculated, and the occurrences are divided into multiple categories through a process known as discretization. For example, all numbers between 1.0 and 3.5 might be classified as one state, and all numbers between 3.5 and 6 might be classified in another. The thresholds for each state are based on the mean and standard deviation of the observed data, and are recalculated every time learning occurs, so even though some amount of accuracy is lost by discretization, the states chosen should usually be well-adapted to the data in your domain (assuming it is somewhat normally distributed). This variable type makes it much easier to work with numeric data by dynamically adapting to your data and handling the discretization for you.
The following example shows a network that uses these advanced variable types:
net = Sbn::Net('Budget Category Network') category = Sbn::Variable(net, :category, [0.5, 0.25, 0.25], [:gas, :food, :clothing]) amount = Sbn::NumericVariable(net, :amount) merchant = Sbn::StringVariable(net, :merchant) category.add_child(amount) category.add_child(merchant)
Before parameter learning occurs on this network, it looks like this:
The Category variable represents a budget category for a financial transaction. The Amount variable is for the amount of the transaction and the Merchant variable handles observed strings for the merchant where the transaction took place. Suppose we supplied some sample points to this network:
net.add_sample_point :category => :gas, :amount => 29.11, :merchant => 'Chevron'
After adding that sample point, the network would look something like this:
The variables with dashed edges are the string covariables that were created by the managing string variable when it saw a new string in the sample points. At present, string variables generate ngrams of length 3, 6, and 10 characters. It is anticipated that these lengths will become customizable in a future release.
There are many areas where we hope to improve Simple Bayesian Networks. Here are some of the possible improvements that may be added in future releases:
-
Support for exact inference
-
Support for continuous variables
-
Saving the sample points along with the network when saving to XMLBIF
-
Speedier inference using native C++ with vectorization provided by macstl
-
Speedier inference through parallelization
-
Support for inference of variable relationships from sample points
-
Support for customizing the number of iterations in the MCMC algorithm (currently hard-coded)
-
Support for customizing the size of ngrams used in string variables
-
Support for intelligently determining the best number of iterations for MCMC at runtime based on the desired level of precision
Please share your own ideas with us and help to improve this library.