Generalized Hilbert ("gilbert") space-filling curve for rectangular domains of arbitrary (non-power of two) sizes.
The discrete Hilbert curve is a widely used space-filling curve to map between N-dimensional and 1-D spaces while preserving locality. However, classical algorithms only work for domains whose sides are powers of two.
We present a simple recursive algorithm that generalizes the Hilbert curve to rectangles of arbitrary sizes in 2D, and cuboids of even sizes in 3D.
A 2D algorithm that combines Peano (3x3) and Hilbert (2x2) blocks was published by Lutz Tautenhahn in 2003:
[1] Lutz Tautenhahn: Draw a Space-Filling Curve of Arbitrary Size, http://lutanho.net/pic2html/draw_sfc.html, 2003.
However, this algorithm is complex and would be very difficult to generalize to 3D. Another aproach that focuses on evaluation speed is described in
[2] Zhang J., Kamata S., Ueshige Y.: A Pseudo-Hilbert Scan Algorithm for Arbitrarily-Sized Rectangle Region, IWICPAS 2006.
This method generalizes to 3D, but it is again complex and the resulting curves are a bit uneven.
The idea is to recursively apply the following template to obtain a Hilbert-like curve. A general rectangle with a known orientation is split into three regions ("up", "right", "down"), for which the function calls itself recursively, until a trivial path can be produced.
The trick is to avoid odd sizes when halving the dimensions (a/2, b/2). The reason is that if the width of a rectangle is odd and its height is even, it is impossible to generate a continuous path that goes from the lower left corner to the lower right corner. In such a case, at least one "diagonal" step needs to be inserted, and the algorithm tries to avoid that whenever it can. Since there is usually some freedom in positioning the horizontal split, the algorithm increments the length "b/2" by one if it happens to be odd. That way, the "up" and "down" rectangles are easier to fill correctly.
There is also the case of a long "right" step, which is resolved by two recursions only in the same direction. In this case, the length "a/2" is chosen to be even. If there ever is a situation where the diagonal step cannot be avoided, it will happen in the top right corner of the original domain.
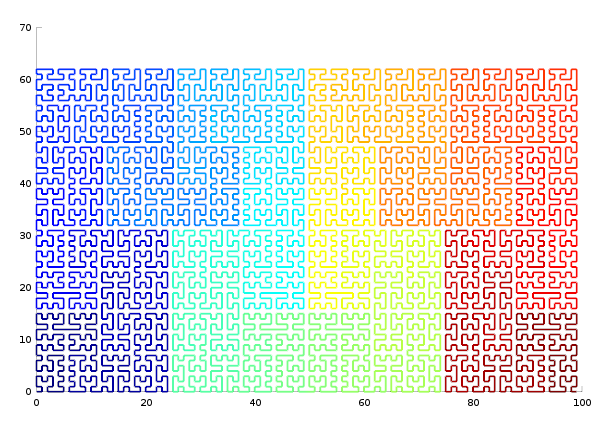
Running gilbert2d with two arguments (width, height) produces a space-filling
curve with orthogonal steps only, as long as the width is even (100x63 shown):
If the sizes are powers of two, a standard Hilbert curve is generated. The algorithm extends naturally to 3D (8x6x4):
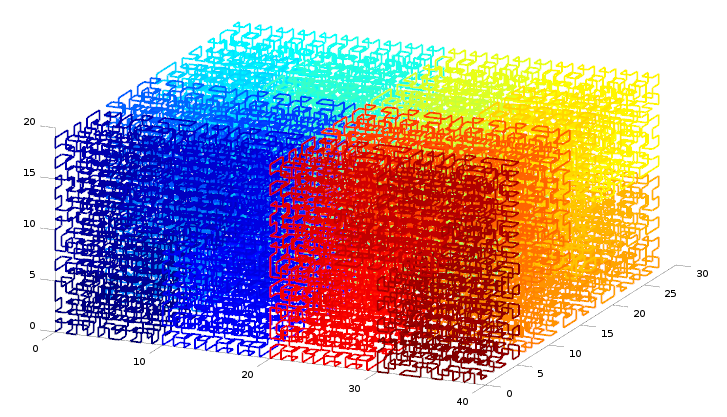
40x30x20:
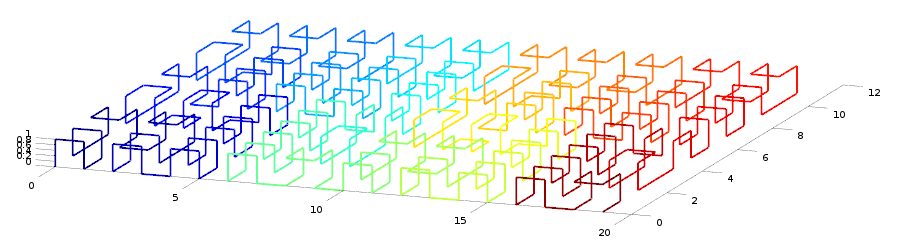
Very flat is OK too (20x12x2):
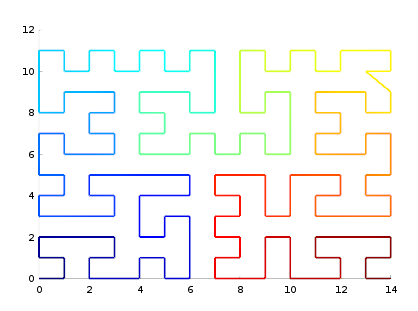
In 2D, if the larger dimension is odd and the smaller is even, a single diagonal step cannot be avoided (15x12):
In 3D this is much worse, so odd dimensions should not be used (7x6x4):
A simple Octave script (plotpath.m) is included to help visualize the
coordinates produced by gilbert2d and gilbert3d. The above figures were
obtained with
./gilbert2d.py 100 63 | octave --eval 'waitfor(plotpath(dlmread(stdin())));'
Author: Jakub Červený. This code is released under the 2-clause BSD license.