python-physics

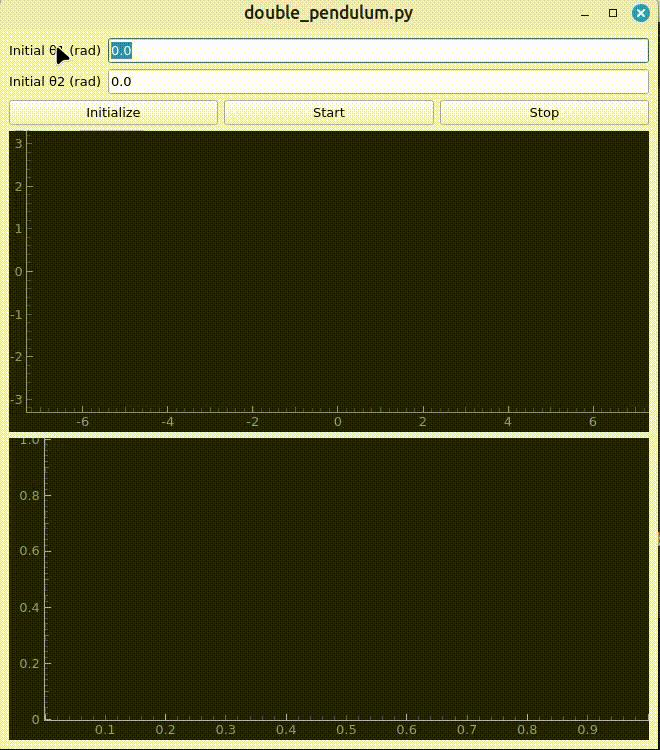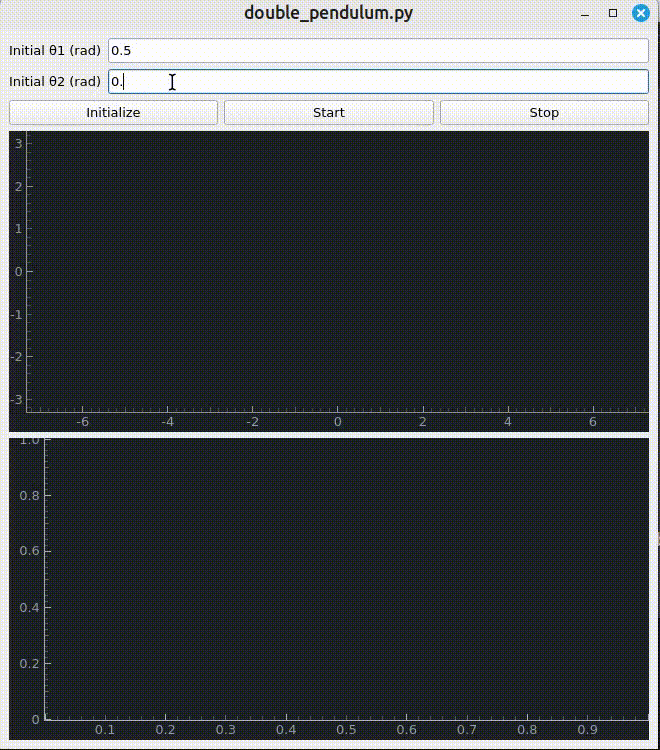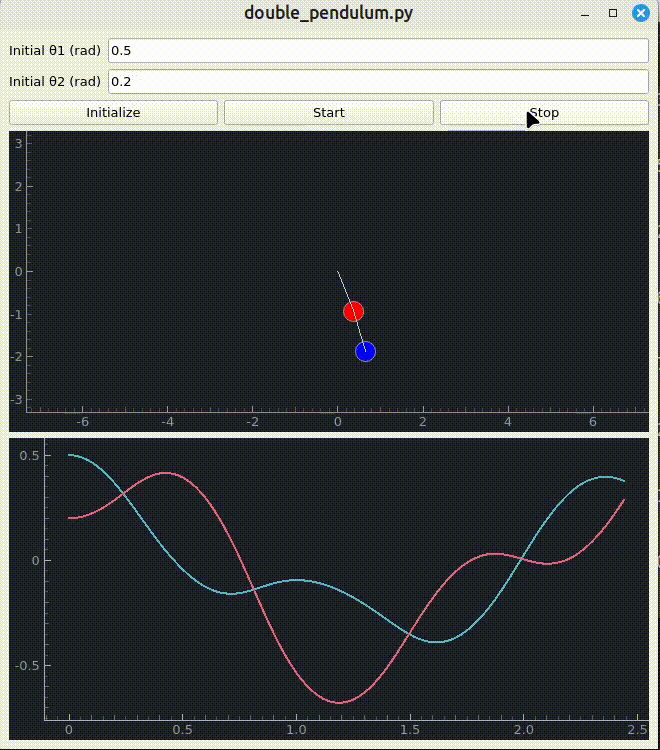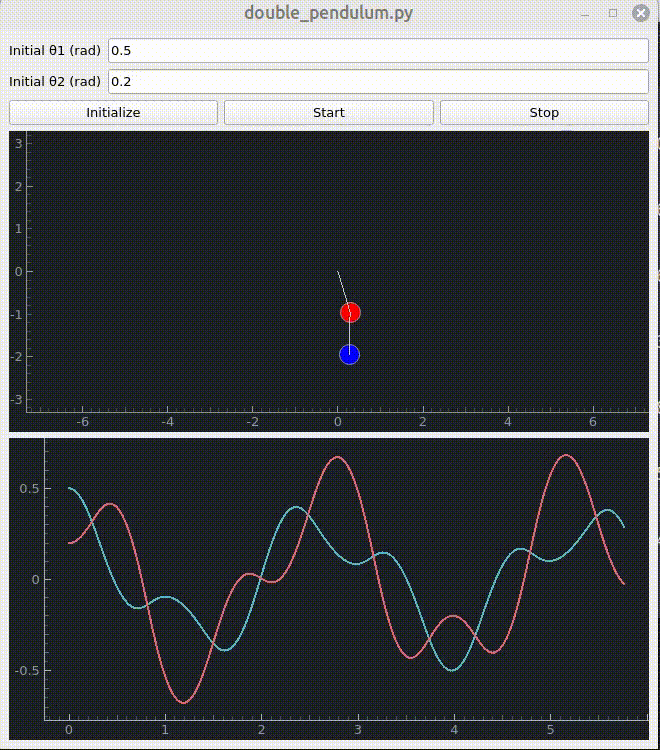
The goal of this project is to build a set of composable tools for solving physics problems. There should be a smooth transition between the symbolic problem and the numerical problem.

Example

import sys
import numpy as np
from scipy.integrate import solve_ivp
from python_physics.vizualization.simulation_framework import create_simulation_framework

from PyQt5.QtWidgets import QApplication, QMainWindow, QVBoxLayout, QHBoxLayout, QFormLayout, QLineEdit, QPushButton, QLabel, QWidget
from PyQt5.QtCore import QTimer


def double_pendulum_ode(t, state, l1, l2, m1, m2, g):
    theta1, theta1_dot, theta2, theta2_dot = state
    delta = theta2 - theta1
    denom1 = (m1 + m2) * l1 - m2 * l1 * np.cos(delta)**2
    denom2 = (l2 / l1) * denom1

    theta1_ddot = (
        m2 * l1 * theta1_dot**2 * np.sin(delta) * np.cos(delta)
        + m2 * g * np.sin(theta2) * np.cos(delta)
        + m2 * l2 * theta2_dot**2 * np.sin(delta)
        - (m1 + m2) * g * np.sin(theta1)
    ) / denom1

    theta2_ddot = (
        -m2 * l2 * theta2_dot**2 * np.sin(delta) * np.cos(delta)
        + (m1 + m2) * g * np.sin(theta1) * np.cos(delta)
        - (m1 + m2) * l1 * theta1_dot**2 * np.sin(delta)
        - (m1 + m2) * g * np.sin(theta2)
    ) / denom2

    return [theta1_dot, theta1_ddot, theta2_dot, theta2_ddot]


def double_pendulum_positions(state, **kwargs):
    l1 = kwargs["l1"]  # Extract l1
    l2 = kwargs["l2"]  # Extract l2
    theta1, _, theta2, _ = state

    x1, y1 = l1 * np.sin(theta1), -l1 * np.cos(theta1)
    x2, y2 = x1 + l2 * np.sin(theta2), y1 - l2 * np.cos(theta2)
    return [x1, y1, x2, y2]


def create_double_pendulum_simulation():
    l1, l2, m1, m2, g = 1.0, 1.0, 1.0, 1.0, 9.81
    dt = 0.02
    default_state = [np.pi / 4, 0.0, np.pi / 6, 0.0]  # Ensure 4 elements

    # Define step simulation function
    def step_simulation(state, t, l1, l2, m1, m2, g):
        # Define the time range for the solver
        t_span = [t, t + dt]
        print(f"Step simulation state: {state}")
        # Use solve_ivp to compute the next state
        sol = solve_ivp(
            fun=lambda t, y: double_pendulum_ode(t, y, l1, l2, m1, m2, g),
            t_span=t_span,
            y0=state,
            t_eval=[t + dt]  # Evaluate at the next time step
        )
        return sol.y[:, -1]  # Return the state at the next time step

    return create_simulation_framework(
        step_simulation=step_simulation,
        transform_positions=double_pendulum_positions,
        default_state=default_state,
        dt=dt,
        params={"l1": l1, "l2": l2, "m1": m1, "m2": m2, "g": g},
        animation_range=(-3, 3),
        input_labels=["Initial θ1 (rad)", "Initial θ2 (rad)"],
        plot_labels=[("θ1(t)", "#56b6c2"), ("θ2(t)", "#e06c75")],
    )


if __name__ == "__main__":
    app = QApplication(sys.argv)  # QApplication must be instantiated first
    simulation = create_double_pendulum_simulation()
    gui = simulation["gui"]

    # Timer for simulation updates
    timer = QTimer()

    # Connect buttons to their respective actions
    gui["buttons"]["initialize"].clicked.connect(
        lambda: (print("Initialize clicked"), simulation["initialize"](gui["inputs"]))
    )
    gui["buttons"]["start"].clicked.connect(
        lambda: (print("Start clicked"), simulation["start"](timer))
    )
    gui["buttons"]["stop"].clicked.connect(
        lambda: (print("Stop clicked"), simulation["stop"](timer))
    )

    # Connect the timer to the simulation runner
    timer.timeout.connect(
        lambda: simulation["run"](timer, gui["animation_items"], gui["plot_items"])
    )

    # Create and display the main window
    window = QMainWindow()
    container = QWidget()
    container.setLayout(gui["layout"])
    window.setCentralWidget(container)
    window.show()

    print("GUI is ready. Waiting for user interaction...")  # Debug
    sys.exit(app.exec_())