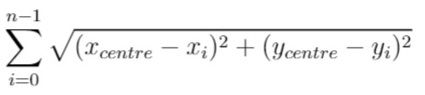一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标,并希望能够以此为依据为新的服务中心选址:使服务中心 到所有客户的欧几里得距离的总和最小 。
给你一个数组 positions ,其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置,返回到所有客户的 欧几里得距离的最小总和 。
换句话说,请你为服务中心选址,该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值:
与真实值误差在 10^-5 之内的答案将被视作正确答案。
示例 1:
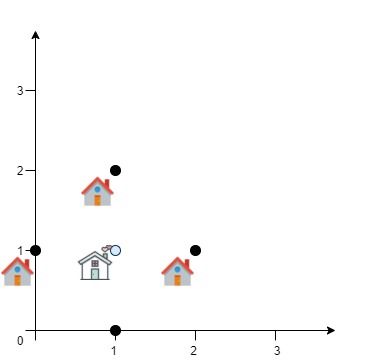
输入:positions = [[0,1],[1,0],[1,2],[2,1]] 输出:4.00000 解释:如图所示,你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置,这样一来到每个客户的距离就都是 1,所有距离之和为 4 ,这也是可以找到的最小值。
示例 2:
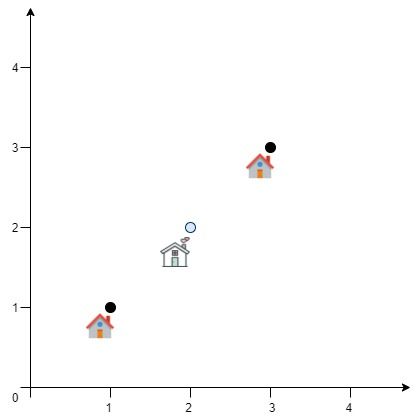
输入:positions = [[1,1],[3,3]] 输出:2.82843 解释:欧几里得距离可能的最小总和为 sqrt(2) + sqrt(2) = 2.82843
示例 3:
输入:positions = [[1,1]] 输出:0.00000
示例 4:
输入:positions = [[1,1],[0,0],[2,0]] 输出:2.73205 解释:乍一看,你可能会将中心定在 [1, 0] 并期待能够得到最小总和,但是如果选址在 [1, 0] 距离总和为 3 如果将位置选在 [1.0, 0.5773502711] ,距离总和将会变为 2.73205 当心精度问题!
示例 5:
输入:positions = [[0,1],[3,2],[4,5],[7,6],[8,9],[11,1],[2,12]] 输出:32.94036 解释:你可以用 [4.3460852395, 4.9813795505] 作为新中心的位置
提示:
1 <= positions.length <= 50positions[i].length == 20 <= positions[i][0], positions[i][1] <= 100