Skip to content

Unary Logical Graph Operators

Jump to bottom Edit New page
Kevin Klein edited this page Nov 8, 2018 · 55 revisions

This section provides an overview of unary graph to graph operators, which consume one graph as input.

Unary Logical Graph Operators
Aggregation
Pattern Matching
Transformation
Property transformation
Grouping
Subgraph
Sampling
Group by RollUp

Aggregation

In general, aggregation operators are used to combine N values into a single one. In the case of Gradoop, they are used to reduce some kind of information that is contained in a graph down to a single value. The aggregate operator is implemented as aggregate() function for the LogicalGraph class. It takes any amount of aggregate functions as an input and outputs the original graph with the result of each aggregate function as a new property. Most aggregate functions require a string denoting the name of the property or label they are being applied to. In the following, they shall be referred to as [propertyName] or [labelName]. Gradoop provides the following aggregate functions:

Function Description Returns
MaxVertexProperty Aggregate function computing the maximum of a specified property over all vertices LogicalGraph with the aggregated property max_[propertyName]: [value]
MinVertexProperty Aggregate function computing the minimum of a specified property over all vertices. LogicalGraph with the aggregated property min_[propertyName]: [value]
MaxEdgeProperty Aggregate function computing the maximum of a specified property over all edges LogicalGraph with the aggregated property max_[propertyName]: [value]
MinEdgeProperty Aggregate function computing the minimum of a specified property over all edges LogicalGraph with the aggregated property min_[propertyName]: [value]
SumEdgeProperty Aggregate function calculates the sum of a specified property over all edges LogicalGraph with the aggregated property sum_[propertyName]: [value]
SumVertexProperty Aggregate function calculates the sum of a specified property over all vertices LogicalGraph with the aggregated property sum_[propertyName]: [value]
EdgeCount Aggregate function computing the edge count of a graph LogicalGraph with the aggregated property edgeCount: [integer]
VertexCount Aggregate function computing the vertex count of a graph LogicalGraph with the aggregated property vertexCount: [integer]
HasEdgeLabel Aggregate and filter function to check presence of an edge label in a graph LogicalGraph with the aggregated property hasEdgeLabel_[labelName]: [bool]
HasVertexLabel Aggregate and filter function to check presence of an vertex label in a graph LogicalGraph with the aggregated property hasVertexLabel_[labelName]: [bool]

Aggregate example

Consider the social graph from our quickstart section. Now we could use the aggregate function to get some more insights into the information that is contained in that graph. For example, we could be interested in the mean age of all persons. To achieve that we would

  1. extract a sub-graph containing only the vertices labeled "Person"
  2. aggregate the sum of all the persons ages
  3. perform a graph head transformation to add the quotient of the summed up ages and the total amount of persons to the graph head
// Given the graph n1 from quickstart, we can aggregate the age values and output the result
SumVertexProperty sumPropertyAge = new SumVertexProperty("age");
LogicalGraph meanAgeAggregation =
  n1
    .subgraph(v -> v.getLabel().equals("Person"), e -> true)
    .aggregate(sumPropertyAge, new VertexCount())
    .transformGraphHead(new TransformationFunction<GraphHead>() {
      @Override
      public GraphHead apply(GraphHead graphHead, GraphHead el1) {
        int sumAge = graphHead.getPropertyValue("sum_age").getInt();
        Long numPerson = graphHead.getPropertyValue("vertexCount").getLong();
        graphHead.setProperty("meanAge", (double) sumAge / numPerson);
        return graphHead;
      }
    });

The resulting graph has the following structure:

n1:graph { meanAge: 30.8, vertexCount: 5, sum_age: 154, } [
  (p1:Person {name: "Bob", age: 24})-[:friendsWith]->(p2:Person{name: "Alice", age: 30})-[:friendsWith]->(p1)
  (p2)-[:friendsWith]->(p3:Person {name: "Jacob", age: 27})-[:friendsWith]->(p2)
  (p3)-[:friendsWith]->(p4:Person{name: "Marc", age: 40})-[:friendsWith]->(p3)
  (p4)-[:friendsWith]->(p5:Person{name: "Sara", age: 33})-[:friendsWith]->(p4)
]

Pattern Matching

In graph analytics, pattern matching is one of the most important and challenging tasks. The LogicalGraph class implements the method query to apply Cypher queries on the data graph. The method returns a GraphCollection containing the matching subgraphs.

query()

The method applies an engine that uses vertex homomorphism and edge isomorphism as default morphism strategies. As pattern matching is the purpose of this method, only the MATCH and WHERE keywords of the Cypher query language are supported. The vertex and edge data of the data graph elements is attached to the resulting vertices. In its more simple forms, the method uses no statistics about the data graph which may result in bad runtime performance. Use GraphStatistics to provide statistics for the query planner. The query method is overloaded. The following table describes each form of the method in detail:

Signature Description
query(String query) Simplest form. Works as described above
query(String query, String constructionPattern) Allows for the creation of new graph elements based on variable bindings of the match pattern
query(String query, GraphStatistics graphStatistics) Allows handling of existing graph statistics
query(String query, String constructionPattern, GraphStatistics graphStatistics) Allows for both the creation of new graph elements as well as the application of existing graph statistics
query(String query, boolean attachData, MatchStrategy vertexStrategy, MatchStrategy edgeStrategy, GraphStatistics graphStatistics) If attachData is set to true, the original vertex and edge data is attached to the result. Possible match strategies are ISOMORPHISM and HOMOMORPHISM
query(String query, String constructionPattern, boolean attachData, MatchStrategy vertexStrategy, MatchStrategy edgeStrategy, GraphStatistics graphStatistics) Same as above with the additional possibility to define a construction pattern

Pattern matching example using Cypher query language

Consider the social graph form the quickstart. Say, we are interested in analyzing Marc's circle of friends. Using the cypher method, we could define a pattern which describes the relation "friend of Marc"

String cypherQuery = "MATCH (a:Person)-[e0:friendsWith]->(b:Person)-[e1:friendsWith]->(c:Person)," +
      " (c)-[e2:friendsWith]->(b)-[e3:friendsWith]->(a)" +
      " WHERE a <> c AND b.name = \"Marc\"";

GraphCollection friendsOfMarc = n1.query(cypherQuery);

The query above results in the following graph collection:

gc[
    g0:graph[
	(a:Person {name: Sara, age: 33})-[:friendsWith]->(b:Person {name: Marc, age:40})-[:friendsWith]->(c:Person {name: Jacob, age:27}),
	(c)-[:friendsWith]->(b)-[:friendsWith]->(a)
    ],
    g1:graph[
	(a:Person {name: Jacob, age: 33})-[:friendsWith]->(b:Person {name: Marc, age:40})-[:friendsWith]->(c:Person {name: Sara, age:27}),
	(c)-[:friendsWith]->(b)-[:friendsWith]->(a)
    ]
]

A useful feature of the query method is the ability to define new graph elements based on variable bindings of the match pattern. Let's define a new relation between Marc's friends called 'acquaintance':

Note: It is necessary to define the new element with an assigned variable. This could change in the future.

String cypherQuery = "MATCH (a:Person)-[e0:friendsWith]->(b:Person)-[e1:friendsWith]->(c:Person)," +
      " (c)-[e2:friendsWith]->(b)-[e3:friendsWith]->(a)" +
      " WHERE a <> c AND b.name = \"Marc\"";

String constructionPattern = "(b)<-[e0]-(a)-[e_new0:acquaintance]->(c)<-[e1]-(b)," +
      " (c)-[e_new1:acquaintance]->(a)," +
      " (c)-[e2]->(b)-[e3]->(a)";

GraphCollection acquaintances = n1.query(cypherQuery, constructionPattern);

Resulting graph collection:

gc[
    g0:graph[
	(a:Person {name: Sara, age: 33})-[:friendsWith]->(b:Person {name: Marc, age:40})-[:friendsWith]->(c:Person {name: Jacob, age:27}),
	(c)-[:friendsWith]->(b)-[:friendsWith]->(a),
	(a)-[:acquaintance]->(c)-[:acquaintance]->(a)
    ],
    g1:graph[
	(a:Person {name: Jacob, age: 33})-[:friendsWith]->(b:Person {name: Marc, age:40})-[:friendsWith]->(c:Person {name: Sara, age:27}),
	(c)-[:friendsWith]->(b)-[:friendsWith]->(a),
	(c)-[:acquaintance]->(a)-[:acquaintance]->(c)
    ]
]

Transformation

By using the transformation operation on a LogicalGraph, one can alter elements of a given graph. This alteration can either affect the graph-head, edges or vertices. One could also think of a Gradoop transformation as a modification to a LogicalGraph that changes an EPGM elements data, but not its identity or the topological structure of the graph.

Every transformation method of the LogicalGraph expects a TransformationFunction as input. This interface defines a method called apply. The method takes the current version of the element and a copy of that element as input. The copy is initialized with the current structural information (i.e. identifiers, graph membership, source / target identifiers). The implementation is able to transform the element by either updating the current version and returning it or by adding necessary information to the new entity and returning it.

The following transformation functions are defined as methods for the LogicalGraph class:

Function Description Expects
transform Transforms the elements of the logical graph using the given transformation functions. TransformationFunction<GraphHead>, TransformationFunction<Vertex>, TransformationFunction<Edge>
transformGraphHead Transforms the graph head of the logical graph using the given transformation function. TransformationFunction<GraphHead>
transformVertices Transforms the vertices of the logical graph using the given transformation function. TransformationFunction<Vertex>
transformEdges Transforms the edges of the logical graph using the given transformation function. TransformationFunction<Edge>

Transformation example

Consider the social graph from the quickstart example. Suppose every person from the graph g1 attended the same university. We could add this new information to the graph like this:

TransformationFunction<Vertex> addPropertyUni = new TransformationFunction<Vertex>() {
      @Override
      public Vertex apply(Vertex vertex, Vertex el1) {
        vertex.setProperty("university", "Leipzig University");
        return vertex;
      }
    };

LogicalGraph n1WithUni = n1
  .subgraph(v -> v.getLabel().equals("Person"), e -> true)
  .transformVertices(addPropertyUni);

The resulting graph has the following structure:

g1:graph[
	(p1:Person {name: "Bob", age: 24, university: "University Leipzig"})-[:friendsWith]->(p2:Person{name: "Alice", age: 30, university: "University Leipzig"})-[:friendsWith]->(p1)
  (p2)-[:friendsWith]->(p3:Person {name: "Jacob", age: 27, university: "University Leipzig"})-[:friendsWith]->(p2)
 	(p3)-[:friendsWith]->(p4:Person{name: "Marc", age: 40, university: "University Leipzig"})-[:friendsWith]->(p3)
  (p4)-[:friendsWith]->(p5:Person{name: "Sara", age: 33, university: "University Leipzig"})-[:friendsWith]->(p4)
]

Property transformation

The property transformation operation is a convenience function for a Transformation on properties. This alteration can either affect the properties of graph-head, edges or vertices.

Every property transformation method of the LogicalGraph expects a PropertyTransformationFunction as input. This interface defines a method called execute. The method takes the current version of the PropertyValue as input. The implementation is able to transform the PropertyValue by updating the current version and returning it.

The following property transformation functions are defined as methods for the LogicalGraph class:

Function Description Expects
transformGraphHeadProperties Transforms the value of a graphHead property matching the specified property key using the given transformation functions. String propertyKey, PropertyTransformationFunction
transformVertexProperties Transforms the value of a vertex property matching the specified property key using the given transformation functions. String propertyKey, PropertyTransformationFunction
transformEdgeProperties Transforms the value of an edge property matching the specified property key using the given transformation functions. String propertyKey, PropertyTransformationFunction

Property transformation example

Consider the social graph from the quickstart example. Suppose that we want to round the age of every person from the graph g1. We could update the age property like this:

PropertyTransformationFunction roundPropertyAge = new PropertyTransformationFunction() {
      @Override
      public PropertyValue execute(PropertyValue value) {
        value.setLong((Long)(Math.round(value.getLong()/10.0) * 10));
        return value;
      }
    };

LogicalGraph n1WithRoundedAge = n1
  .subgraph(v -> v.getLabel().equals("Person"), e -> true)
  .transformVertexProperties("age", roundPropertyAge);

The resulting graph has the following structure:

g1:graph[
	(p1:Person {name: "Bob", age: 20})-[:friendsWith]->(p2:Person{name: "Alice", age: 30})-[:friendsWith]->(p1)
  (p2)-[:friendsWith]->(p3:Person {name: "Jacob", age: 30})-[:friendsWith]->(p2)
 	(p3)-[:friendsWith]->(p4:Person{name: "Marc", age: 40})-[:friendsWith]->(p3)
  (p4)-[:friendsWith]->(p5:Person{name: "Sara", age: 30})-[:friendsWith]->(p4)
]

Grouping

By using the grouping operator you can achieve a structural grouping of vertices and edges to condense a graph and thus help to uncover insights about patterns and statistics hidden in the graph.

Strategies

Gradoop defines the following two strategies applicable for grouping: GROUP_REDUCE and GROUP_COMBINE. By default GROUP_REDUCE is used.

In some cases with bad distribution of vertex grouping keys it may be desirable to combine vertex tuples using a CombineGroup transformation to potentially reduce network traffic. This behaviour is represented by the GROUP_COMBINE strategy. For more information see this.

Functions

For grouping any of the following functions can be applied to a LogicalGraph object.

Function Description Expects
groupBy Groups vertices based on the given vertex grouping keys which can be property keys or labels. List<String> vertexGroupingKeys
groupBy Groups vertices and edges based on the given grouping keys which can be property keys or labels. List<String> vertexGroupingKeys,
List<String> edgeGroupingKeys
groupBy Groups vertices and edges based on the given grouping keys which can be property keys or labels. Additionally aggregates are calculated using the given aggregator functions (MaxAggregator, MinAggregator, SumAggregator) and a strategy has to be chosen. List<String> vertexGroupingKeys,
List<PropertyValueAggregator> vertexAggregateFunctions,
List<String> edgeGroupingKeys,
List<PropertyValueAggregator> edgeAggregateFunctions, GroupingStrategy groupingStrategy

Grouping example

Consider the social graph from the quickstart example. For our grouping example we will first extract all nodes of type Person and then calculate a rounded age which we are going to use for grouping:

LogicalGraph preprocessedGraph = n1
  .vertexInducedSubgraph(new ByLabel<>("Person"))
  .transformVertices(new TransformationFunction<Vertex>() {
      @Override
      public Vertex apply(Vertex vertex, Vertex el1) {
        int age = vertex.getPropertyValue("age").getInt();
        vertex.setProperty("age_rounded", (int)MathUtils.round(age, -1));
        return vertex;
      }
    });
LogicalGraph summarizedGraph = preprocessedGraph
  .groupBy(Arrays.asList(Grouping.LABEL_SYMBOL, "age_rounded")),
    singletonList(new CountAggregator("count")),
    singletonList(Grouping.LABEL_SYMBOL),
    singletonList(new CountAggregator("count")),
    GroupingStrategy.GROUP_REDUCE);

The resulting graph is shown below the next example.

Grouping example using GroupingBuilder

Alternatively you can use the GroupingBuilder which offers more options. The following example leads to the same result as the traditional grouping operation shown above.

// Perform grouping on preprocessedGraph
LogicalGraph summarizedGraph = new Grouping.GroupingBuilder()
  .setStrategy(GroupingStrategy.GROUP_REDUCE)
  .addVertexGroupingKey("age_rounded")
  .useVertexLabel(true)
  .useEdgeLabel(true)
  .addVertexAggregator(new CountAggregator())
  .addEdgeAggregator(new CountAggregator())
  .build()
  .execute(preprocessedGraph);

The resulting graph has the following structure:

Label Groups

Imagine we would not have used a transformation function to remove nodes which are not of type Person, but still want to group over our age_rounded property for those nodes. For this job we could define a VertexLabelGroup as the following example shows:

// Perform grouping on preprocessedGraph
LogicalGraph summarizedGraph = new Grouping.GroupingBuilder()
  .setStrategy(GroupingStrategy.GROUP_REDUCE)
  .useVertexLabel(true)
  .useEdgeLabel(true)
  .addVertexLabelGroup("Person", "PersonAge", Arrays.asList("age_rounded"), Arrays.asList(new CountAggregator()))
  .build()
  .execute(preprocessedGraph);

This would lead to the following resulting graph:

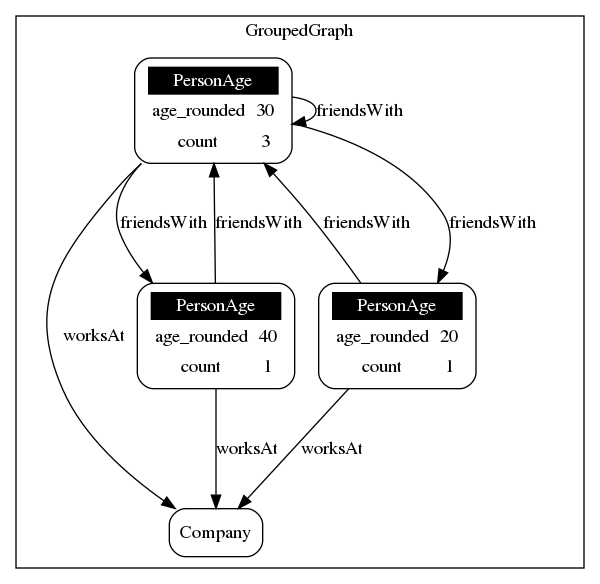
For adding a VertexLabelGroup you can use one of the following four functions:

Function Description Expects
addVertexLabelGroup Groups vertices with the specified label based on the given grouping keys which can be property keys or labels. String label,
List<String> groupingKeys
addVertexLabelGroup Groups vertices with the specified label based on the given grouping keys which can be property keys or labels. Super vertices are created using the supplied super vertex label. String label,
String superVertexLabel,
List<String> groupingKeys
addVertexLabelGroup Groups vertices with the specified label based on the given grouping keys which can be property keys or labels and calculate aggregates using the supplied aggregator functions. String label,
List<String> groupingKeys, List<PropertyValueAggregator> aggregators
addVertexLabelGroup Groups vertices with the specified label based on the given grouping keys which can be property keys or labels and calculate aggregates using the supplied aggregator functions. Super vertices are created using the supplied super vertex label. String label,
String superVertexLabel,
List<String> groupingKeys, List<PropertyValueAggregator> aggregators

This could be applied analogously for edges using an EdgeLabelGroup.

Subgraph

A subgraph is a logical graph which contains only vertices and edges that fulfill a given vertex and/or edge predicate. The associated operators are implemented as functions .subgraph(), .vertexInducedSubgraph() and .edgeInducedSubgraph() that can be called on a LogicalGraph instance. The former allows one of five available execution strategies to be defined, which are listed in the table below.

Strategy Description
Subgraph.Strategy.BOTH Applies both filter functions on the input vertex and edge data set. This is the standard strategy of the .subgraph() function. Note, that this operator does not verify the consistency of the resulting graph.
Subgraph.Strategy.BOTH_VERIFIED Applies both filter functions on the input vertex and edge data set. In addition, this strategy verifies the consistency of the output graph.
Subgraph.Strategy.VERTEX_INDUCED Only applies the vertex filter function and adds the incident edges connecting those vertices via a join. This strategy is applied by the .vertexInducedSubgraph() function.
Subgraph.Strategy.EDGE_INDUCED Only applies the edge filter function and computes the connecting vertices. This strategy is applied by the .edgeInducedSubgraph() function.
Subgraph.Strategy.EDGE_INDUCED_PROJECT_FIRST Only applies the edge filter function and computes the resulting vertices via: DISTINCT((π_source(E) U π_target(E))) |><| V

Frequently used filter expressions are predefined in Gradoop. The following table gives an overview of them and defines whether they can be used as filters for vertices (V) or edges (E) or both.

Predefined Filter Applicable for Description
True<>() V,E Filter function represents logical true.
False<>() V,E Filter function represents logical false.
LabelIsIn<>(String... labels) V,E Filter function to check if an EPGM element's label is in the defined white list.
ByLabel<>(String label) V,E Filter function to check if an EPGM element's label is equal to the defined one.
BySameId<>(GradoopId id) V,E Filters elements if their identifier is equal to the given identifier.
ByDifferentId<>(GradoopId id) V,E Filters elements if their identifier is not equal to the given identifier.
ByTargetId<>(GradoopId id) E Filters edges having the specified target vertex id.
BySourceId<>(GradoopId id) E Filters edges having the specified source vertex id.
ByProperty<>(Property prop)
ByProperty<>(String key)
ByProperty<>(String key, PropertyValue value) 		V,E Filter function to check if an EPGM element has a property with the specified key or key value combination.
InNoGraph<>() V,E This filter returns true, if the element has not graph ids.
InGraph<>(GradoopId graphId) V,E This filter returns true, if the element is contained in a graph specified by its id.
InAnyGraph<>(GradoopIdSet graphIds) V,E This filter returns true, if an element is contained in any of a set of given graphs.
InAllGraphs<>(GradoopIdSet graphIds) V,E This filter returns true, if an element is contained in all of a set of given graphs.
VertexRandomFilter<>(float sampleSize, long randomSeed) V Creates a random value for each vertex and filters those that are below a given threshold.

These filters (and other filters implementing the CombinableFilter interface) may be combined using a logical and/or or inverted using a logical not:

Filter Combination Resulting Filter
filter.and(otherFilter) Filters filter and otherFilter combined using a logical and, returns a filter accepting objects accepted by both filters.
filter.or(otherFilter) Filters filter and otherFilter combined using a logical or, returns a filter accepting objects accepted by at least one of the filters.
filter.negate() Filter filter inverted using a logical not, returns a filter accepting objects not accepted by the original filter.
new And<>(filter1, filter2, ...) Combine an arbitrary number of filters filter1, filter2, ... using a logical and. This is semantically equivalent to filter1.and(filter2).and(....
new Or<>(filter1, filter2, ...) Combine an arbitrary number of filters filter1, filter2, ... using a logical or. This is semantically equivalent to filter1.or(filter2).or(....

Subgraph example

The following code shows examples of the different subgraph functions and the use of combined filters:

// Apply vertex and edge filter to the given graph n1 from quickstart
LogicalGraph subgraph = n1
    .subgraph(
        new LabelIsIn<>("Person", "Company"),
        new ByLabel<>("worksAt")
    );

// Apply vertex and edge filter with verifying the consistency (no "Company" vertices included)
LogicalGraph verifiedSubgraph = n1
    .subgraph(
        new LabelIsIn<>("Person", "Company"),
        new ByLabel<>("friendsWith")
        Subgraph.Strategy.BOTH_VERIFIED
    );

// Apply only a vertex filter function
LogicalGraph vertexInduced = n1
    .vertexInducedSubgraph(new ByProperty<>("age"));

// Apply only a edge filter function
LogicalGraph edgeInduced = n1
    .edgeInducedSubgraph(new BySourceId<>(myGradoopId));

// Apply a combined vertex filter function:
LogicalGraph fromCombinedFilters = n1
    .vertexInducedSubgraph(
        new ByLabel<Vertex>("Person").and(new ByProperty<>("Name", PropertyValue.create("Marc")).negate())
            .or(new ByLabel<>("Company")));

Sampling

Graph sampling is a technique to pick a subset of vertices and/or edges from the original graph. This can be used to obtain a smaller graph if the whole graph is known or, if the graph is unknown, to explore the graph. The provided techniques are either vertex based, edge based, traversal based or a combination of these. They are implemented as operators for Gradoops LogicalGraph and return the sampled graph. The following sampling methods are provided:

Method Description
RandomVertexSampling Computes a vertex sampling of the graph. Retains randomly chosen vertices of a given relative amount. Retains all edges which source- and target-vertices were chosen. There may retain some unconnected vertices in the sampled graph.
Parameters:
sampleSize: relative amount of vertices in the sampled graph
randomSeed: seed-value for the random number generator
RandomNonUniformVertexSampling Computes a vertex sampling of the graph. Retains randomly chosen vertices of a given relative amount and all edges which source- and target-vertices were chosen. A degree-dependent value is taken into account to have a bias towards high-degree vertices. There may retain some unconnected vertices in the sampled graph.
Parameters:
sampleSize: relative amount of vertices in the sampled graph
randomSeed: seed-value for the random number generator
RandomLimitedDegreeVertexSampling Computes a vertex sampling of the graph. Retains all vertices with a degree greater than a given degree threshold and degree type. Also retains randomly chosen vertices with a degree smaller or equal this threshold. Retains all edges which source- and target-vertices were chosen.
Parameters:
sampleSize: relative amount of vertices with degree smaller or equal the given degreeThreshold
randomSeed: seed-value for the random number generator
degreeThreshold: threshold for degrees of sampled vertices
degreeType: type of degree considered for sampling, see VertexDegree
RandomVertexNeighborhoodSampling Computes a vertex sampling of the graph. Retains randomly chosen vertices of a given relative amount and includes all neighbors of those vertices in the sampling. Retains all edges which source- and target-vertices were chosen.
Parameters:
sampleSize: relative amount of vertices in the sampled graph
randomSeed: seed-value for the random number generator
neighborType: type of neighborhood considered for sampling, see Neighborhood
RandomEdgeSampling Computes an edge sampling of the graph. Retains randomly chosen edges of a given relative amount and their associated source- and target-vertices. No unconnected vertices will retain in the sampled graph.
Parameters:
sampleSize: relative amount of vertices in the sampled graph
randomSeed: seed-value for the random number generator
RandomVertexEdgeSampling Computes an edge sampling of the graph. First selects randomly chosen vertices of a given relative amount and all edges which source- and target-vertices were chosen. Then randomly chooses edges of a given relative amount from this set of edges and their associated source- and target-vertices. No unconnected vertices will retain in the sampled graph.
Parameters:
vertexSampleSize: relative amount of vertices in the sampled graph
edgeSampleSize: relative amount of edges in the sampled graph
randomSeed: seed-value for the random number generator
vertexEdgeSamplingType: can be simple, nonUniform or nonUniformHybrid
PageRankSampling Computes a PageRank-Sampling of the graph. Uses the Gradoop-Wrapper of Flinks PageRank-algorithm. Retains all vertices with a PageRank-score greater or equal/smaller than a given sampling threshold - depending on the Parameters set. If all vertices got the same PageRank-score, it can be decided whether to sample all vertices or none of them. Retains all edges which source- and target-vertices were chosen. There may retain some unconnected vertices in the sampled graph.
Parameters:
dampeningFactor: probability of following an out-link, otherwise jump to a random vertex
maxIteration: maximum number of algorithm iterations
threshold: threshold for the PageRank-score, determining if a vertex is sampled, e.g. 0.5
sampleGreaterThanThreshold: sample vertices with a PageRank-score greater (true) or equal/smaller (false) the threshold
keepVerticesIfSameScore: sample all vertices (true) or none of them (false), if all got the same PageRank-score

Sampling example for RandomLimitedDegreeVertexSampling

// read the original graph
LogicalGraph graph = readLogicalGraph("path/to/graph", "json");

// define sampling parameters
float sampleSize = 0.3; // retain vertex with degree smaller or equal degreeThreshold with a probability of 30%
long randomSeed = 0L; // random seed can be 0
long degreeThreshold = 3L; // sample all vertices with degree of degreeType greater than 3
VertexDegree degreeType = VertexDegree.IN // consider in-degree for sampling

// call sampling method
LogicalGraph sample = new RandomLimitedDegreeVertexSampling(
      sampleSize, randomSeed, degreeThreshold, degreeType)).sample(graph);

Group by RollUp

The rollUp operation allows aggregations at multiple levels using a single query.

The operator can be used by instantiating the class directly with the desired options or by calling one of the shown convenience methods of LogicalGraph:

Function Description Returns
groupVerticesByRollUp Runs rollUp operation with changing aggregation level via varying combinations of vertex grouping keys. GraphCollection with the differently grouped graphs
groupEdgesByRollUp Runs rollUp operation with changing aggregation level via varying combinations of edge grouping keys. GraphCollection with the differently grouped graphs

Both methods require the same parameters:

  1. A list containing the vertex property keys used for grouping.
  2. A list of property value aggregators used for grouping on vertices.
  3. A list containing the edge property keys used for grouping.
  4. A list of property value aggregators used for grouping on edges.

For the following examples, consider a graph containing persons as vertices and phone calls between those persons as edges. Vertices do contain the country, state and city as separate properties and edges, on the other hand, the time of calling with year, month, day, hour and minute as separate properties.

The following code would lead to a graph collection containing graphs grouped by {(:label, country, state, city), (:label, country, state), (:label, country), (:label)}. You would be able to see how many persons initiated a phone call living in the exact same city, state, country and for all persons using a single query.

// Apply vertex based rollUp on previously described graph
List<String> vertexGroupingKeys =
  Arrays.asList(Grouping.LABEL_SYMBOL, "country", "state", "city");
List<PropertyValueAggregator> vertexAggregators =
  Collections.singletonList(new CountAggregator("count"));
List<String> edgeGroupingKeys = Collections.emptyList();
List<PropertyValueAggregator> edgeAggregators = Collections.emptyList();

GraphCollection output =
  n1.groupVerticesByRollUp(
    vertexGroupingKeys,
    vertexAggregators,
    edgeGroupingKeys,
    edgeAggregators);

Analogously the following code would lead to an edge based rollUp and therefore to a graph collection containing graphs grouped by {(year, month, day, hour, minute), (year, month, day, hour), (year, month, day), (year, month), (year)}. You would be able to see how many persons initiated a phone call within the exact same minute, hour, on the same day, month and year.

// Apply edge based rollUp on previously described graph
List<String> vertexGroupingKeys = Collections.emptyList();
List<PropertyValueAggregator> vertexAggregators = Collections.emptyList();
List<String> edgeGroupingKeys =
  Arrays.asList("year", "month", "day", "hour", "minute");
List<PropertyValueAggregator> edgeAggregators =
  Collections.singletonList(new CountAggregator("count"));

GraphCollection output =
  n1.groupVerticesByRollUp(
    vertexGroupingKeys,
    vertexAggregators,
    edgeGroupingKeys,
    edgeAggregators);
Add a custom footer
Gradoop

Home

Getting Started

Examples

Data Model

Temporal Graph Support

Sources and Sinks

Graph Operators

Graph Analyzing Algorithms

Gradoop Store

Changelog

JavaDoc (Snapshot)

Clone this wiki locally