Projet de Régression Linéaire

Ce projet a pour but de démontrer l'application de la régression linéaire à l'analyse de données. Nous examinerons les concepts de la régression linéaire, de l'analyse du dataset, de la standardisation des données et de la performance du modèle.

Table des matières

1. La régression linéaire 1.1 Le modèle 1.2 Les erreurs du modèle 1.3 Gradient 1.4 Évaluation du modèle
2. Analyse du Dataset 2.1 Affichage de la forme du DataFrame 2.2 Statistiques descriptives 2.3 Vérification des valeurs manquantes 2.4 Les colonnes existantes 2.5 Analyse de la corrélation entre les variables 2.6 Traitement du shape

---

La régression linéaire

La régression linéaire est une technique d'apprentissage automatique qui modélise une relation linéaire entre les variables d'entrée et une variable de sortie continue.

Le modele

On implémente un modèle selon l'équation matricielle $\displaystyle F=X.θ$ et puis on teste le modèle initiale défini par la valeur initiale de $\displaystyle θ$ qu'on a initialisé d'une manière aléatoire.

Les erreurs du modele

On mesure les erreurs du modele sur le Dataset X, y en implémenterl'erreur quadratique moyenne.

$$ \displaystyle J(θ) = \frac{1}{2m} \sum_{i=1}^{m} (h_{θ}(x^{(i)}) - y^{(i)})^{2} \\ h_{θ}(x) = θ^{T}x = θ_{0} + θ_{1}x_{1} $$

Gradient

On implémente la formule du gradient pour la MSE

$$ \frac{\partial J(θ)}{\partial θ} = \frac{1}{m} X^{T}.(X.θ - y) $$

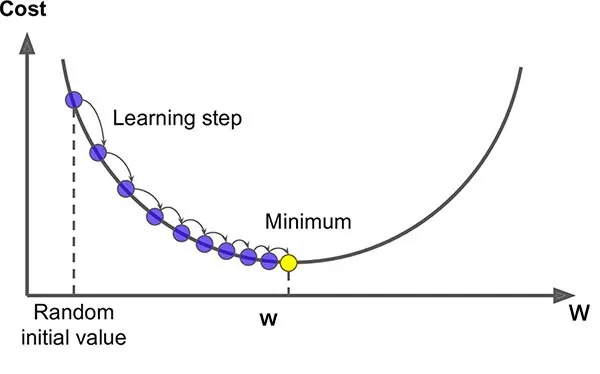
et par la suite on utilise cette fonction dans la descente de gradient:

$$ \displaystyle θ = θ - \alpha \frac{\partial J(θ)}{\partial θ} $$

Evaluation du modèle

Evaluation du modèle - Coefficient de détermination
RSE : RELATIVE Squared Error (L'erreur carrée relative) :

$$ RSE = \frac{\sum_{i=1}^{m} (f(x_{i}) - y_{i})^{2}}{\sum_{i=1}^{m} \left(y - \frac{1}{m}\sum_{j=1}^{m} y_{j}\right)^{2}} $$

le complement à 1 de la $\displaystyle RSE$ et le coefficient de mdetermination noté $\displaystyle R^{2}$ Tel que : $\displaystyle R^{2} = 1 - RSE$. Le modèle idéale donne $\displaystyle R^{2} = 1$