README.md

comments	difficulty	edit_url	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/0500-0599/0542.01%20Matrix/README.md	广度优先搜索 数组 动态规划 矩阵

542. 01 矩阵

English Version

题目描述

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

 

示例 1：

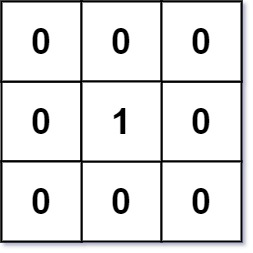
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

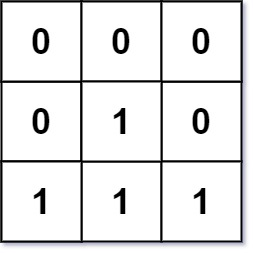
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

 

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 104
• 1 <= m * n <= 104
• mat[i][j] is either 0 or 1.
• mat 中至少有一个 0 

解法

方法一：BFS

我们创建一个大小和 $\textit{mat}$ 一样的矩阵 $\textit{ans}$，并将所有的元素初始化为 $-1$。

然后我们遍历 $\textit{mat}$，将所有的 $0$ 元素的坐标 $(i, j)$ 加入队列 $\textit{q}$，并将 $\textit{ans}[i][j]$ 设为 $0$。

接下来，我们使用广度优先搜索，从队列中取出一个元素 $(i, j)$，并遍历其四个方向，如果该方向的元素 $(x, y)$ 满足 $0 \leq x < m$, $0 \leq y < n$ 且 $\textit{ans}[x][y] = -1$，则将 $\textit{ans}[x][y]$ 设为 $\textit{ans}[i][j] + 1$，并将 $(x, y)$ 加入队列 $\textit{q}$。

最后返回 $\textit{ans}$。

时间复杂度 $O(m \times n)$，空间复杂度 $O(m \times n)$。其中 $m$ 和 $n$ 分别为矩阵 $\textit{mat}$ 的行数和列数。

Python3

class Solution:
    def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
        m, n = len(mat), len(mat[0])
        ans = [[-1] * n for _ in range(m)]
        q = deque()
        for i, row in enumerate(mat):
            for j, x in enumerate(row):
                if x == 0:
                    ans[i][j] = 0
                    q.append((i, j))
        dirs = (-1, 0, 1, 0, -1)
        while q:
            i, j = q.popleft()
            for a, b in pairwise(dirs):
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n and ans[x][y] == -1:
                    ans[x][y] = ans[i][j] + 1
                    q.append((x, y))
        return ans

Java

class Solution {
    public int[][] updateMatrix(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[][] ans = new int[m][n];
        for (int[] row : ans) {
            Arrays.fill(row, -1);
        }
        Deque<int[]> q = new ArrayDeque<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    q.offer(new int[] {i, j});
                    ans[i][j] = 0;
                }
            }
        }
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!q.isEmpty()) {
            int[] p = q.poll();
            int i = p[0], j = p[1];
            for (int k = 0; k < 4; ++k) {
                int x = i + dirs[k], y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[i][j] + 1;
                    q.offer(new int[] {x, y});
                }
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> ans(m, vector<int>(n, -1));
        queue<pair<int, int>> q;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 0) {
                    ans[i][j] = 0;
                    q.emplace(i, j);
                }
            }
        }
        vector<int> dirs = {-1, 0, 1, 0, -1};
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            for (int i = 0; i < 4; ++i) {
                int x = p.first + dirs[i];
                int y = p.second + dirs[i + 1];
                if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1) {
                    ans[x][y] = ans[p.first][p.second] + 1;
                    q.emplace(x, y);
                }
            }
        }
        return ans;
    }
};

Go

func updateMatrix(mat [][]int) [][]int {
	m, n := len(mat), len(mat[0])
	ans := make([][]int, m)
	for i := range ans {
		ans[i] = make([]int, n)
		for j := range ans[i] {
			ans[i][j] = -1
		}
	}
	type pair struct{ x, y int }
	var q []pair
	for i, row := range mat {
		for j, v := range row {
			if v == 0 {
				ans[i][j] = 0
				q = append(q, pair{i, j})
			}
		}
	}
	dirs := []int{-1, 0, 1, 0, -1}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		for i := 0; i < 4; i++ {
			x, y := p.x+dirs[i], p.y+dirs[i+1]
			if x >= 0 && x < m && y >= 0 && y < n && ans[x][y] == -1 {
				ans[x][y] = ans[p.x][p.y] + 1
				q = append(q, pair{x, y})
			}
		}
	}
	return ans
}

TypeScript

function updateMatrix(mat: number[][]): number[][] {
    const [m, n] = [mat.length, mat[0].length];
    const ans: number[][] = Array.from({ length: m }, () => Array.from({ length: n }, () => -1));
    const q: [number, number][] = [];
    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            if (mat[i][j] === 0) {
                q.push([i, j]);
                ans[i][j] = 0;
            }
        }
    }
    const dirs: number[] = [-1, 0, 1, 0, -1];
    for (const [i, j] of q) {
        for (let k = 0; k < 4; ++k) {
            const [x, y] = [i + dirs[k], j + dirs[k + 1]];
            if (x >= 0 && x < m && y >= 0 && y < n && ans[x][y] === -1) {
                ans[x][y] = ans[i][j] + 1;
                q.push([x, y]);
            }
        }
    }
    return ans;
}

Rust

use std::collections::VecDeque;

impl Solution {
    pub fn update_matrix(mat: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
        let m = mat.len();
        let n = mat[0].len();
        let mut ans = vec![vec![-1; n]; m];
        let mut q = VecDeque::new();

        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 0 {
                    q.push_back((i, j));
                    ans[i][j] = 0;
                }
            }
        }

        let dirs = [-1, 0, 1, 0, -1];
        while let Some((i, j)) = q.pop_front() {
            for k in 0..4 {
                let x = i as isize + dirs[k];
                let y = j as isize + dirs[k + 1];
                if x >= 0 && x < m as isize && y >= 0 && y < n as isize {
                    let x = x as usize;
                    let y = y as usize;
                    if ans[x][y] == -1 {
                        ans[x][y] = ans[i][j] + 1;
                        q.push_back((x, y));
                    }
                }
            }
        }

        ans
    }
}