Agradeço a Deus primeiramente por essa oprtunidade de poder continuar estudando o que eu mais gosto de fazer, que é programar. Agradeços a minha familía ,minha eposa e filha e meus pais.
Isso é dedicado aos amigos que sempre me apoiaram aos estudos e com muita gentileza me proporcionam uma motivação para continuar nessa linha reta.
Fontes de estudo.: https://pt.wikipedia.org/wiki/Rudolf_Bayer https://github.com/barbaraneves/estrutura-de-dados-avancada-2017-1/tree/master/ProjetosEDA/Rubro-Negra https://youtu.be/_lTz-ePzWjk [[ED] Aula 107 - Implementando uma Árvore Rubro Negra ] https://pt.wikipedia.org/wiki/%C3%81rvore_rubro-negra [ wikipedia ] https://pages.cs.wisc.edu/~paton/readings/Red-Black-Trees/ [ James Paton. «Red-Black Trees» ]
O Estudo de Algoritmos para resolução de problemas de arvores sempre me fascinou, mas sempre o codifiquei em outras linguagens como por exemplo FORTRAn que é uma linguagem muito boa para codificação mais algoritma, por ser uma linguagem com muito poder computacional científico. O Desafio de estudar e aplicar isso dentro da minha zona de conforto em objetoPascal, é com certeza muito interessantee só amplia mais meu conhecimento e minhas técnicas para otimização. Estudar a RBT é um desafio adicional em Objectpacal, e é um cenário interessante para alicar e desenvolver isso com instruções diretas a registradores em determinados pontos codificando isso em uma linguagem mais próxima da máquina como Assembly.
Nesse desafio, o foco é aplicar meus conhecimentos em uma linguagem que estou familiarizado, mas ao mesmo tempo, mergulhar em novos conceitos e técnicas para a implementação eficiente de uma RBT. Acredito que ao dominar essa estrutura de dados e algoritmo, estarei melhor preparado para enfrentar problemas complexos e desenvolver soluções mais eficientes em minha área de atuação.
Cada passo nessa jornada de aprendizado e aplicação da RBT em Object Pascal é uma oportunidade de crescimento e enriquecimento do meu repertório técnico. Estou entusiasmado para enfrentar esse desafio e descobrir as soluções criativas e eficientes que posso desenvolver "mergulhando de cabeça" nesse conhecimento fascinante.
Árvore Rubro-Negra é uma estrutura de dados utilizada para armazenar e organizar informações de forma hierárquica. Ela é uma variação da árvore binária de busca, o que significa que cada nó possui no máximo dois filhos: um filho à esquerda e um filho à direita.
O que torna a RBT especial é a aplicação de um conjunto de regras que garantem seu balanceamento e, consequentemente, a sua eficiência na realização de operações de busca, inserção e remoção de elementos. Essas regras são simples e garantem que a altura da árvore seja sempre proporcional ao logaritmo do número de elementos presentes, o que torna as operações praticamente tão rápidas quanto em uma árvore perfeitamente balanceada.
Penso em utilizar instruções inline Assembly X86 em operações SIMD para otimização aos acesos e manipulações, com registradores temporários para o swap na Arvore, acredito que a minha motivação parte de um contexto de que se essas operações puderem ocorrer sem a alta camada de abstrações da linguagem , teria um código menos propenso gerando um trabalho mais preguçoso para o Front-End do compilador, e teria menos custo computacional para o Back_End do compilador otimizar essas operações.
Estudando o livro de algoritmos estruturados aplicados a ciência da computação em fortran percebi que algumas operações algumas operações de por exemplo remover O Nó da árvore e depois ter que reindexar novamente para se adequar a estrutura da árvore rubro-negra há um custo computacional de uma complexidade considerável e que acredito que isso de uma forma mais inline - contígua , se torne mais eficiente com menos processamento e custo de processmento e até mesmo custo para Representação IR .
Portanto tenho que pensar em algumas coisas como
Portabilidade, Manutenção e iteroperabilidade .
Rudolf Bayer é um cientista da computação alemão conhecido por suas contribuições significativas no campo da ciência da computação e estruturas de dados. Ele nasceu em 1943 na Alemanha. Bayer obteve seu doutorado em ciência da computação pela Universidade de Karlsruhe, onde desenvolveu seus primeiros trabalhos de pesquisa.
Uma das contribuições mais importantes de Rudolf Bayer foi a co-invenção da Árvore Rubro-Negra, Arvore B e outros algoritmos para otimização de grafos, juntamente com seu colega cientista da computação, Volker Strassen, em 1972. Essa estrutura de dados é amplamente utilizada para implementar árvores de busca binária balanceadas, garantindo uma complexidade de tempo eficiente para operações como busca, inserção e remoção de elementos.
Bayer recebeu seu Ph.D. (1966) da Universidade de Illinois. Depois de trabalhar no Boeing Research Labs, ele se tornou professor associado na Purdue University. Ele era professor de informática na Universidade Técnica de Muenchen desde 1972 e chefe do Grupo de Pesquisa Knowledge Bases no Bavarian Research Centre for Knowledge Based Systems (FORWISS).
Ele prestou consultoria para IBM, Siemens, Amdahl, DEC, Deutsche Telekom e foi professor visitante na IBM, XEROX PARC e em várias universidades no Japão, Austrália, Estados Unidos e Cingapura.
Ele é cofundador da TransAction SW GmbH e detém duas patentes. Ele é o vencedor de 2001 ACM SIGMOD Edgar F. Codd Innovations Award e German Federal Cross of Merit. Seus interesses de pesquisa incluem estruturas de dados, sistemas de banco de dados, bibliotecas digitais e armazenamento de dados.
Bayer definiu alguns aspectos essenciais para que uma arvore pode ser classificada como ARN.
As regras da ARN são as seguintes:
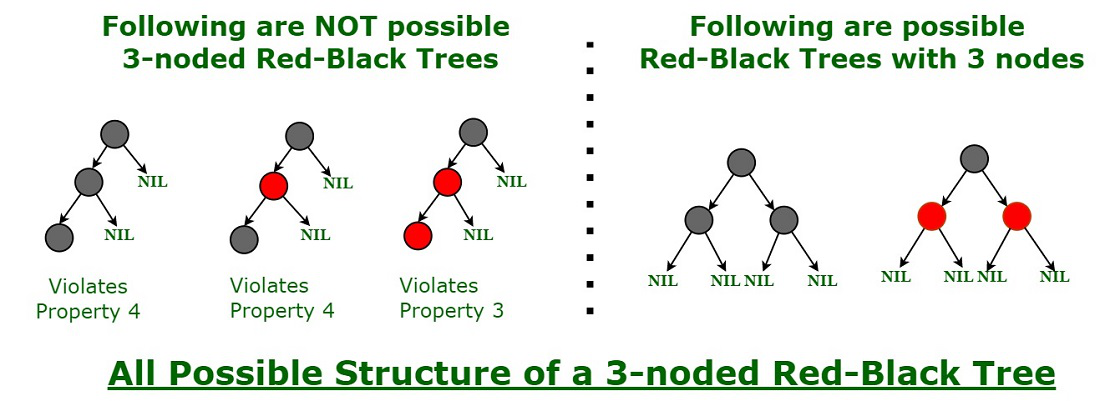
Cada nó é colorido, podendo ser vermelho ou preto.
- A raiz da árvore é sempre preta.
- Todos os nós folhas (nós sem filhos) são considerados pretos e não armazenam informações (por convenção, são considerados sentinelas).
- Se um nó é vermelho, seus filhos devem ser pretos.
- Todos os caminhos a partir de um nó até seus nós folhas descendentes contêm o mesmo número de nós pretos.
- Durante o processo de inserção e exclusão, siga as regras para manter uma disposição diferente dessas cores
Essas regras garantem que a árvore permaneça relativamente equilibrada mesmo após inserções ou remoções, evitando casos extremos de desbalanceamento que poderiam prejudicar o desempenho das operações.
As principais vantagens da Árvore Rubro-Negra são sua capacidade de manter-se balanceada e sua eficiência em operações de busca, inserção e remoção, todas com complexidade O(log n), onde "n" é o número de elementos na árvore.
Ao entender e implementar uma Árvore Rubro-Negra em Object Pascal, como tenho buscado fazer, podemos explorar os conceitos por trás dessa estrutura e aplicá-la em diversos cenários, como otimização de algoritmos e resolução de problemas complexos
O chamado equilíbrio da árvore significa que o número de descendentes esquerdos de cada nó na árvore deve ser aproximadamente igual ao número de descendentes à sua direita (não exatamente o mesmo número).
Para árvores binárias compostas de números aleatórios, geralmente é aproximadamente equilibrado, mas para dados sequenciais, pode levar a um desequilíbrio extremo de árvores binárias. Nos casos mais extremos, ele até degenerará em uma lista, momento em que a complexidade do tempo degenerará para O(n), em vez do O(logn) da árvore balanceada.
Quando uma árvore binária não está devidamente balanceada, como no caso de uma árvore binária de busca que contém dados sequenciais em ordem crescente ou decrescente, pode ocorrer um desequilíbrio extremo que leva a uma estrutura parecida com uma lista linear.
Essa situação, conhecida como "árvore degenerada" ou "árvore não balanceada", é problemática porque faz com que as operações de busca, inserção e remoção se tornem ineficientes, já que a altura da árvore deixa de ser logarítmica em relação ao número de elementos e se aproxima de um crescimento linear. Ou seja, em vez de uma complexidade de tempo O(log n), a complexidade torna-se O(n), onde "n" é o número de elementos na árvore.
Quando ocorre essa degeneração, a árvore deixa de ser uma estrutura eficiente para a realização das operações usuais e perde a vantagem de ser uma árvore binária de busca balanceada.
Em uma Árvore Rubro-Negra (ARN), cada nó é associado a uma cor, que pode ser vermelha ou preta. Essa cor é uma propriedade adicional que é usada para garantir o equilíbrio e a eficiência da árvore durante as operações de inserção e remoção.
A ideia por trás das cores é impor algumas regras especiais que devem ser seguidas para manter a árvore sempre balanceada. Essas regras são projetadas de forma que a altura da árvore seja mantida proporcional ao logaritmo do número de elementos, o que permite operações rápidas, com complexidade O(log n).
Uma árvore de pesquisa binária que satisfaz as regras de uma árvore ARN provavelmente ficaria assim de uma forma bem otimizada perceba que os nós são identificados por cores e essas cores elas ajudam a identificar com melhor velocidade, os valores contidos em cada nó para uma busca mais otimizada.
As operações de rotação são operações fundamentais em Árvores Rubro-Negras e outras árvores binárias balanceadas. Elas são usadas para preservar a propriedade de balanceamento da árvore após a inserção ou remoção de nós. Existem dois tipos de rotações: rotação à esquerda (left rotation) e rotação à direita (right rotation).
A rotação à esquerda é uma operação que envolve três nós: o nó atual (x), o filho à direita (y) e o neto esquerdo de y (b). Essa operação é usada quando o nó x está desequilibrado para a direita.
x y
/ \ / \
a y --> x c
/ \ / \
b c a bA rotação à direita é o oposto da rotação à esquerda e também envolve três nós: o nó atual (y), o filho à esquerda (x) e o neto direito de x (b). Essa operação é usada quando o nó y está desequilibrado para a esquerda.
y x
/ \ / \
x c --> a y
/ \ / \
a b b cAo inserir ou remover nós em uma Árvore Rubro-Negra, as rotações são aplicadas para ajustar a posição dos nós e preservar as propriedades da árvore, como a altura negra (o número de nós pretos em qualquer caminho da raiz às folhas é o mesmo). Dessa forma, a árvore mantém sua eficiência de busca e outras operações em O(log n) para a maioria das operações, onde n é o número de nós na árvore.
Considere esse esboço ..
Nessa árvore, os nós estão representados com seus valores entre parênteses e a cor de cada nó é indicada entre parênteses também (Preto ou Vermelho). Suponha que precisamos aplicar uma rotação à esquerda no nó 25 para equilibrar a árvore:
O nó atual é o 25 (nó que estamos rotacionando), o filho à direita é o 30 e o neto esquerdo de 30 é nulo (ou seja, não existe). Fazemos a rotação à esquerda, movendo o nó 30 para o lugar do nó 25 e tornando o nó 25 o filho à esquerda do nó 30. A árvore ficará assim:
Em uma Analogia do Mundo real, é como se nós Pegássemos onde queremos rotacionar com os dedos e a arvore se combinasse em cores ordenadas pelos seus valores.seguramos o numero 25 com os dedos e a árvore se moveu para o lado direito.
Algoritmos de inserção para ARN.
A inserção da árvore rubro-negra, a maior parte anterior é a mesma da árvore de busca binária ou seja, do nó raiz para baixo para encontrar a posição do nó a ser inserido, localizar inserir o no, depois de inserir o nó a mais uma operação verificar se a árvore está balanceada se ela está desbalanceada é necessário repará-la para que a árvore fique equilibrada novamente então concluímos que toda vez que temos que inserir um novo nó temos que Equilbra-la.
ao inserir um novo nó este nó é definido como vermelho, por que pode reduzir a probabilidade de violar as regras vermelhas e pretas, depois de inserir o nó vamos então realizar algumas análises.
Se O Nó P do nó inserido estiver preto ou seja estiver em conformidade com a regra nada será feito. Se o Nó P inserido no nó vermelhor e o nó U também for Vermelhor, então transforme o nó G em Vermelho e os nós P e U em Preto. Defina o nó G como sendo o nó Atual e reinicie o ajuste de balanceamento da árvore.
Se o nó P do nóe de inserçã estiver vermelho e o nó U estiver Preto ou ausente e o nó de inserção for o nó filho esquerdo do seu nó P e o nó P for filho esquerdo do nó G, entao gire o nó P para preto e o nó G para vermelho, execute a operação destra do nó G e reinicie o ajuste de banalceamento da árvore.