At minio we use a hash algorithm in order to detect bit rot for data blocks that are stored on disk. Thus far we have been using the Blake2b algorithm but recent developments have led us to do new research for a faster algorithm for bit rot protection.
Initially we looked into SipHash as well as Poly1305. Obviously Poly1305 is not a "traditional" hash function but since it has nice performance properties and could potentially fit our use case (if used in a particular way), we decided to test it out as well.
As a last algorithm we have analysed HighwayHash which has been finalized as of January 2018. It can produce checksums in 64, 128, or 256 bit sizes and significantly outperforms other hashing techniques allowing for speeds over 10GB/sec on a single core (as compared to roughly 1 GB/sec on a single core for Blake2b). We have developed a Golang implementation with accelerations for both Intel and ARM.
Due to the fact that we are interested specifically in bit rot detection, we tried to simulate bit rot by generating messages of varying lengths and by flipping (XOR-ring) a single bit across the full length of the message and computing the hash for each of these permutations. In addition we also run patterns of 2 up to 8 adjacent bits across each byte of each input message.
All hashes are sorted and then the smallest difference is searched for between two consecutive hashes. The number of leading zero bits that this smallest difference has then gives us a measure of how close (or how far apart depending on your point of view) we are to a collision with respect to the size (in number of bits) for the respective hash function.
The following table shows an overview for the number of leading zero bits for the different permutations.
| Permutations | HighwayHash (64) | HighwayHash (128) | HighwayHash (256) | Blake2b (512) | Poly1305 (128) | SipHash (128) |
|---|---|---|---|---|---|---|
| 9216 | 27 | 28 | 28 | 26 | 28 | 29 |
| 18432 | 31 | 28 | 30 | 28 | 31 | 28 |
| 36864 | 33 | 35 | 31 | 33 | 31 | 31 |
| 73728 | 32 | 32 | 31 | 30 | 33 | 31 |
| 147456 | 33 | 34 | 36 | 36 | 33 | 34 |
| 294912 | 37 | 39 | 38 | 36 | 38 | 35 |
| 589824 | 41 | 38 | 37 | 37 | 40 | 39 |
| 1179648 | 37 | 39 | 40 | 41 | 40 | 41 |
| 2359296 | 47 | 43 | 42 | 44 | 41 | 45 |
| 4718592 | 44 | 44 | 45 | 48 | 45 | 45 |
| 9437184 | 48 | 45 | 47 | 46 | 47 | 46 |
| 18874368 | 47 | 48 | 48 | 46 | 48 | 51 |
| 37748736 | 53 | 53 | 49 | 50 | 48 | 51 |
| 75497472 | 52 | 53 | 52 | 51 | 53 | 54 |
| 150994944 | 56 | 53 | 56 | 54 | 54 | 53 |
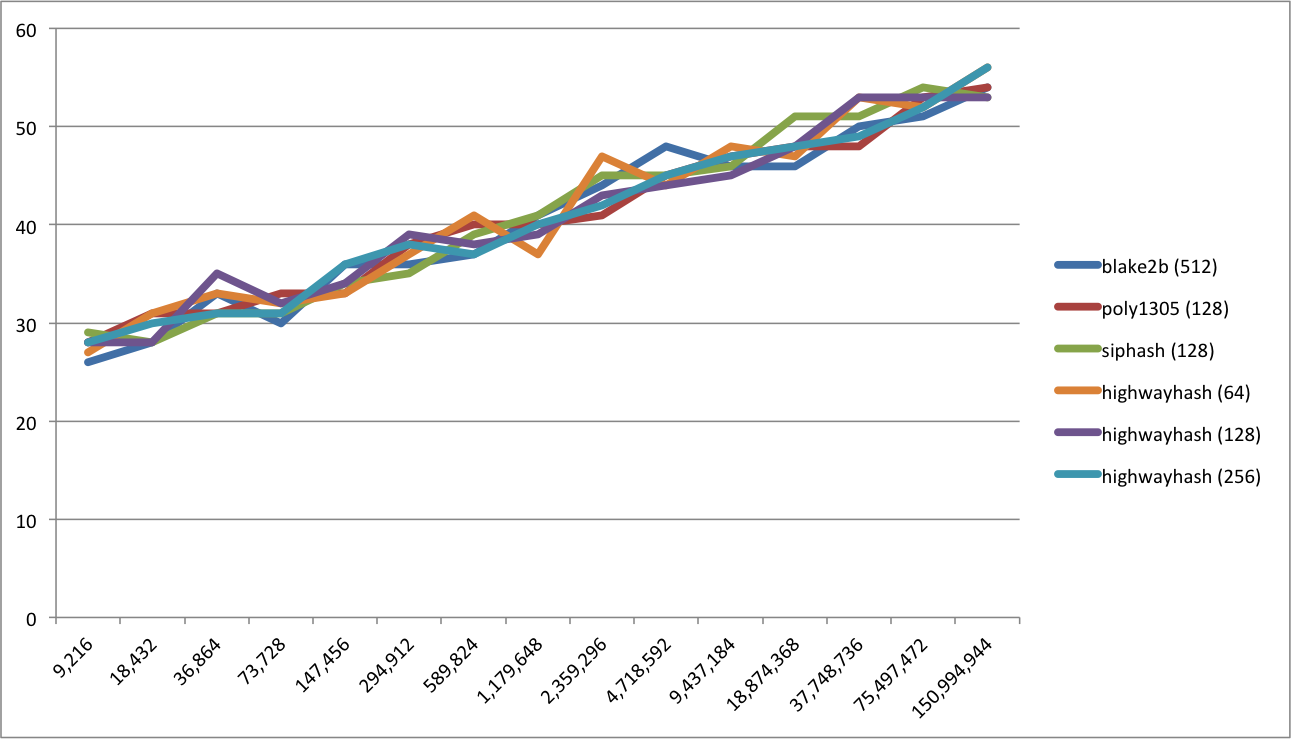
Graphically represented this gives the following overview:
In earlier research with respect to Blake2b we found that for the YFCC100m dataset (Yahoo Flickr Creative Commons 100M) we obtained a closest collision of 52 equal leading bits (at 100 million scale). Thus it is nice to know that for a different type of dataset the results are similar. Note that these were much larger objects and overall took several (combined) weeks of computing power.
While both SipHash and Poly1305 produce good results that could qualify them for bit rot detection, given the fact that they do not outperform HighwayHash means that there is no incentive for switching.
As can be concluded from the results presented above, HighwayHash produces qualitatively similar results as compared to Blake2b. Given the huge performance difference it thus makes sense to switch. That leaves the question which size of output to use.
Clearly the 64 bits version should not be used as it (at 100 million scale) gets "close" (within 10 bits) of the maximum value of 64 bits.
Although the finalization of HighwayHash-128 is slightly faster as compared to HighwayHash-256, that should not be the primary reason for making the decision.
Below are the detailed measurements as executed on dual Skylake CPUs (Xeon Gold 6152 with 22 Core @ 2.1 GHz).
h i g h w a y h a s h 6 4
---Permutations |--- Zero bits | Duration
-----------9216 |---------- 27 | 20.381302ms
----------18432 |---------- 31 | 27.571612ms
----------36864 |---------- 33 | 56.052397ms
----------73728 |---------- 32 | 104.601131ms
---------147456 |---------- 33 | 193.915563ms
---------294912 |---------- 37 | 326.372434ms
---------589824 |---------- 41 | 548.609056ms
--------1179648 |---------- 37 | 1.03530732s
--------2359296 |---------- 47 | 3.544088757s
--------4718592 |---------- 44 | 5.984269238s
--------9437184 |---------- 48 | 13.655630501s
-------18874368 |---------- 47 | 37.100825307s
-------37748736 |---------- 53 | 2m1.893114127s
-------75497472 |---------- 52 | 19m7.856193177s
------150994944 |---------- 56 | 2h27m53.158081067s
h i g h w a y h a s h 1 2 8
---Permutations |--- Zero bits | Duration
-----------9216 |---------- 28 | 12.780649ms
----------18432 |---------- 28 | 30.06254ms
----------36864 |---------- 35 | 68.784714ms
----------73728 |---------- 32 | 105.522995ms
---------147456 |---------- 34 | 226.163161ms
---------294912 |---------- 39 | 420.283355ms
---------589824 |---------- 38 | 663.253149ms
--------1179648 |---------- 39 | 1.432212157s
--------2359296 |---------- 43 | 2.781799607s
--------4718592 |---------- 44 | 6.316052298s
--------9437184 |---------- 45 | 17.407566111s
-------18874368 |---------- 48 | 41.393221202s
-------37748736 |---------- 53 | 2m11.951301187s
-------75497472 |---------- 53 | 19m41.172739809s
------150994944 |---------- 53 | 2h28m44.846577785s
h i g h w a y h a s h 2 5 6
---Permutations |--- Zero bits | Duration
-----------9216 |---------- 28 | 42.702422ms
----------18432 |---------- 30 | 73.954159ms
----------36864 |---------- 31 | 121.332344ms
----------73728 |---------- 31 | 222.526971ms
---------147456 |---------- 36 | 425.226972ms
---------294912 |---------- 38 | 840.404466ms
---------589824 |---------- 37 | 1.544777895s
--------1179648 |---------- 40 | 2.721589884s
--------2359296 |---------- 42 | 4.783848222s
--------4718592 |---------- 45 | 9.457394958s
--------9437184 |---------- 47 | 20.228981718s
-------18874368 |---------- 48 | 51.531855485s
-------37748736 |---------- 49 | 2m26.319665407s
-------75497472 |---------- 52 | 19m53.693452686s
------150994944 |---------- 56 | 2h23m55.834082563s
b l a k e 2 b
---Permutations |--- Zero bits | Duration
-----------9216 |---------- 26 | 61.13945ms
----------18432 |---------- 28 | 111.499262ms
----------36864 |---------- 33 | 189.275791ms
----------73728 |---------- 30 | 331.913372ms
---------147456 |---------- 36 | 692.136065ms
---------294912 |---------- 36 | 1.271843096s
---------589824 |---------- 37 | 2.44415668s
--------1179648 |---------- 41 | 4.454261956s
--------2359296 |---------- 44 | 10.528152825s
--------4718592 |---------- 48 | 28.531043005s
--------9437184 |---------- 46 | 1m28.637419899s
-------18874368 |---------- 46 | 5m7.323075536s
-------37748736 |---------- 50 | 18m59.189679076s
-------75497472 |---------- 51 | 1h13m26.851782323s
------150994944 |---------- 54 | 4h48m46.614104626s
p o l y 1 3 0 5
---Permutations |--- Zero bits | Duration
-----------9216 |---------- 28 | 22.267656ms
----------18432 |---------- 31 | 40.13137ms
----------36864 |---------- 31 | 76.420881ms
----------73728 |---------- 33 | 145.6595ms
---------147456 |---------- 33 | 238.326942ms
---------294912 |---------- 38 | 433.122249ms
---------589824 |---------- 40 | 804.927135ms
--------1179648 |---------- 40 | 1.823510133s
--------2359296 |---------- 41 | 6.213754498s
--------4718592 |---------- 45 | 9.823461941s
--------9437184 |---------- 47 | 26.058247821s
-------18874368 |---------- 48 | 1m21.038484996s
-------37748736 |---------- 48 | 4m37.082124066s
-------75497472 |---------- 53 | 24m55.351343578s
------150994944 |---------- 54 | 2h30m9.271630052s
s i p h a s h
---Permutations |--- Zero bits | Duration
-----------9216 |---------- 29 | 18.267322ms
----------18432 |---------- 28 | 37.565362ms
----------36864 |---------- 31 | 67.701024ms
----------73728 |---------- 31 | 134.268518ms
---------147456 |---------- 34 | 284.326987ms
---------294912 |---------- 35 | 336.299086ms
---------589824 |---------- 39 | 725.117538ms
--------1179648 |---------- 41 | 1.836565811s
--------2359296 |---------- 45 | 4.199563088s
--------4718592 |---------- 45 | 12.092629909s
--------9437184 |---------- 46 | 37.705131584s
-------18874368 |---------- 51 | 2m5.958026812s
-------37748736 |---------- 51 | 7m38.738874946s
-------75497472 |---------- 54 | 30m20.270643374s
------150994944 |---------- 53 | 2h35m57.478741043s