当一个函数在其函数体内调用自身,则称之为递归。最经典的例子便是计算斐波那契数列,即前两个数为1,从第三个数开始每个数均为前两个数之和。
数列如下所示:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, …
下面的程序可用于生成该数列:
package main
import "fmt"
func main() {
result := 0
for i := 0; i <= 10; i++ {
result = fibonacci(i)
fmt.Printf("fibonacci(%d) is: %d\n", i, result)
}
}
func fibonacci(n int) (res int) {
if n <= 1 {
res = 1
} else {
res = fibonacci(n-1) + fibonacci(n-2)
}
return
}输出:
fibonacci(0) is: 1
fibonacci(1) is: 1
fibonacci(2) is: 2
fibonacci(3) is: 3
fibonacci(4) is: 5
fibonacci(5) is: 8
fibonacci(6) is: 13
fibonacci(7) is: 21
fibonacci(8) is: 34
fibonacci(9) is: 55
fibonacci(10) is: 89许多问题都可以使用优雅的递归来解决,比如说著名的快速排序算法。
在使用递归函数时经常会遇到的一个重要问题就是栈溢出:一般出现在大量的递归调用导致的程序栈内存分配耗尽。这个问题可以通过一个名为懒惰求值的技术解决,在 Go 语言中,我们可以使用管道(channel)和 goroutine来实现。
Go 语言中也可以使用相互调用的递归函数:多个函数之间相互调用形成闭环。因为 Go 语言编译器的特殊性,这些函数的声明顺序可以是任意的。下面这个简单的例子展示了函数 odd 和 even 之间的相互调用:
package main
import (
"fmt"
)
func main() {
fmt.Printf("%d is even: is %t\n", 16, even(16)) // 16 is even: is true
fmt.Printf("%d is odd: is %t\n", 17, odd(17))
// 17 is odd: is true
fmt.Printf("%d is odd: is %t\n", 18, odd(18))
// 18 is odd: is false
}
func even(nr int) bool {
if nr == 0 {
return true
}
return odd(RevSign(nr) - 1)
}
func odd(nr int) bool {
if nr == 0 {
return false
}
return even(RevSign(nr) - 1)
}
func RevSign(nr int) int {
if nr < 0 {
return -nr
}
return nr
}转载自:http://www.ruanyifeng.com/blog/2015/04/tail-call.html
函数调用自身,称为递归。如果尾调用自身,就称为尾递归。
递归非常耗费内存,因为需要同时保存成千上百个调用记录,很容易发生"栈溢出"错误(stack overflow)。但对于尾递归来说,由于只存在一个调用记录,所以永远不会发生"栈溢出"错误。
function factorial(n) {
if (n === 1) return 1;
return n * factorial(n - 1);
}
factorial(5) // 120上面代码是一个阶乘函数,计算n的阶乘,最多需要保存n个调用记录,复杂度 O(n) 。
如果改写成尾递归,只保留一个调用记录,复杂度 O(1) 。
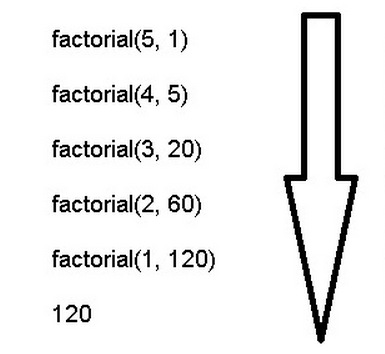
function factorial(n, total) {
if (n === 1) return total;
return factorial(n - 1, n * total);
}
factorial(5, 1) // 120尾递归的实现,往往需要改写递归函数,确保最后一步只调用自身。做到这一点的方法,就是把所有用到的内部变量改写成函数的参数。比如上面的例子,阶乘函数 factorial 需要用到一个中间变量 total ,那就把这个中间变量改写成函数的参数。这样做的缺点就是不太直观,第一眼很难看出来,为什么计算5的阶乘,需要传入两个参数5和1?
两个方法可以解决这个问题。方法一是在尾递归函数之外,再提供一个正常形式的函数。
function tailFactorial(n, total) {
if (n === 1) return total;
return tailFactorial(n - 1, n * total);
}
function factorial(n) {
return tailFactorial(n, 1);
}
factorial(5) // 120上面代码通过一个正常形式的阶乘函数 factorial ,调用尾递归函数 tailFactorial ,看起来就正常多了。
函数式编程有一个概念,叫做柯里化(currying),意思是将多参数的函数转换成单参数的形式。这里也可以使用柯里化。
function currying(fn, n) {
return function (m) {
return fn.call(this, m, n);
};
}
function tailFactorial(n, total) {
if (n === 1) return total;
return tailFactorial(n - 1, n * total);
}
const factorial = currying(tailFactorial, 1);
factorial(5) // 120上面代码通过柯里化,将尾递归函数 tailFactorial 变为只接受1个参数的 factorial 。
第二种方法就简单多了,就是采用ES6的函数默认值。
function factorial(n, total = 1) {
if (n === 1) return total;
return factorial(n - 1, n * total);
}
factorial(5) // 120上面代码中,参数 total 有默认值1,所以调用时不用提供这个值。
总结一下,递归本质上是一种循环操作。纯粹的函数式编程语言没有循环操作命令,所有的循环都用递归实现,这就是为什么尾递归对这些语言极其重要。对于其他支持"尾调用优化"的语言(比如Lua,ES6),只需要知道循环可以用递归代替,而一旦使用递归,就最好使用尾递归。
当在进行大量的计算时,提升性能最直接有效的一种方式就是避免重复计算。通过在内存中缓存和重复利用相同计算的结果,称之为内存缓存。最明显的例子就是生成斐波那契数列的程序:
要计算数列中第 n 个数字,需要先得到之前两个数的值,但很明显绝大多数情况下前两个数的值都是已经计算过的。即每个更后面的数都是基于之前计算结果的重复计算。
而我们要做就是将第 n 个数的值存在数组中索引为 n 的位置,然后在数组中查找是否已经计算过,如果没有找到,则再进行计算。
下面这段程序就是依照这个原则实现的,计算到第 40 位数字的性能对比:
- 普通写法:4.730270 秒
- 内存缓存:0.001000 秒
内存缓存的优势显而易见,而且还可以将它应用到其它类型的计算中,例如使用 map而不是数组或切片:
package main
import (
"fmt"
"time"
)
const LIM = 41
var fibs [LIM]uint64
func main() {
var result uint64 = 0
start := time.Now()
for i := 0; i < LIM; i++ {
result = fibonacci(i)
fmt.Printf("fibonacci(%d) is: %d\n", i, result)
}
end := time.Now()
delta := end.Sub(start)
fmt.Printf("longCalculation took this amount of time: %s\n", delta)
}
func fibonacci(n int) (res uint64) {
// memoization: check if fibonacci(n) is already known in array:
if fibs[n] != 0 {
res = fibs[n]
return
}
if n <= 1 {
res = 1
} else {
res = fibonacci(n-1) + fibonacci(n-2)
}
fibs[n] = res
return
}内存缓存的技术在使用计算成本相对昂贵的函数时非常有用(不仅限于例子中的递归),譬如大量进行相同参数的运算。这种技术还可以应用于纯函数中,即相同输入必定获得相同输出的函数。