RISC-V指令集:2010年开始被研发,是一种基于精简指令集(RISC)原则的开源指令集架构(ISA),有32bit/word和64bit/word之分。在本书中,规定 1word=4byte=32bits
指令的通用方法:
1.使用program counter(PC)获取当前指令位置,在执行完当前指令后,向后移动四个字节来读取下一条指令(PC+4,正好对应1word=32bits的要求)
2.从内存中读取指令,指令会表达该步骤将进行什么操作
3.ALU等将会执行这些操作
Sign Magnitude:原码
Two's Complement:二进制补码
Values of a Binary Number:Interger、Fixed Point Number(定点数)、Floating Point Number(浮点数)
其余已在数逻中学习过
在现代计算机中,整数通常使用二进制补码来表示,这样就可以将减法操作转化为加法操作处理
由于二进制补码可以表示的数的范围为-128~+127,因此可以根据符号位(在某些书中称为负权)判断是否存在溢出现象。
两正数做加法时,如果产生溢出,则溢出进位必然会使符号位变为1,则可以判断其是个负数,不符合常理,因此溢出;
一正一负的数做加法时,不会产生溢出;
两负数做加法时,如果产生溢出,则溢出进位会导致原位(符号位)变为0,则可以判断其为一个正数,不符合常理,因此溢出;
被减数是正数、但减数是负数时,如果产生溢出,则符号位必会溢出为1,则其结果为一个负数,不符合常理,因此溢出;
两数相减为同号时,不会产生溢出;
被减数为负数,但减数为正数时,如果产生溢出,则溢出进位会导致符号位为0,其变为一个正数,不符合常理,因此溢出。
1.ALU会检测是否有溢出发生,并生成异常(Generation of an exception),这会中断程序的正常运行
2.定位:Save the instruction address (not PC) in special register EPC(Exception Program Counter:异常返回地址寄存器,用于存储异常返回的地址)
3.Jump to specific routine in OS(跳转至操作系统中处理异常的指令流)
Correct & return to program(纠正错误)、Return to program with error code (保存现场)、 Abort program(终止程序)
实际上,计算机并没有明确ALU到底包含多少功能,但可以从最基本的功能开始,一步步构建复杂的模块
构成ALU的方式:模块化构建(如增加扩展以支持“加法”功能)、使用“Select”功能实现共享逻辑
构建步骤:从一位操作开始,逐步扩展到多位
数逻中已经提到,在减法转化为加法时只需要将减数取反,并将进位CarryIn设置为1即可实现,因此我们得到了下面的ALU,此ALU具有与、或、加、减四种功能。
在此基础上,我们可以进行进一步的扩展:
slt(set less than)指令:
slt rd,rs,rt 解释:if rs<rt,rd=1,else rd=0
具体操作:使用减法进行比较,(rs-rt):如果结果为负(利用符号位比较):则rs<rt
由上述讨论可以看到,最高位(符号位)在判断溢出、两数比较中十分重要,因此可以将最高位的结果单独作为一个输入组成一个模块,用于判断是否溢出和比较关系。改进后的ALU如下图所示:
以上均为单位ALU的组装,当我们将多个这样的单位ALU组装起来,再进行一些调试,就可以形成一个完全体ALU。构造如下:
特点:并行输入、每位的进位级联在一起、是一种波纹进位加法器(ripple carry adder)
但其有个致命的问题:在两数相等时,无法仅通过最高位判断二者是否相等,因此需要将每一位的结果再通过一个或非门判断相减结果是否均为零(是否相等),改进后的结果如下图所示:
在逻辑设计图中,ALU通常为如下的标志(并不是所有ALU都会有上述所有功能):
运行时间分析:
上述所使用的波纹进位加法器,由于较高的位需要等待较低的位计算出是否需要进位才能输出结果,就像”波纹“一样,因此其所占用时间是很长的。加法需要经过两个异或门,所以消耗时间为两个时钟周期;进位则需要2-3个时钟周期,因此n位波纹进位加法器需要
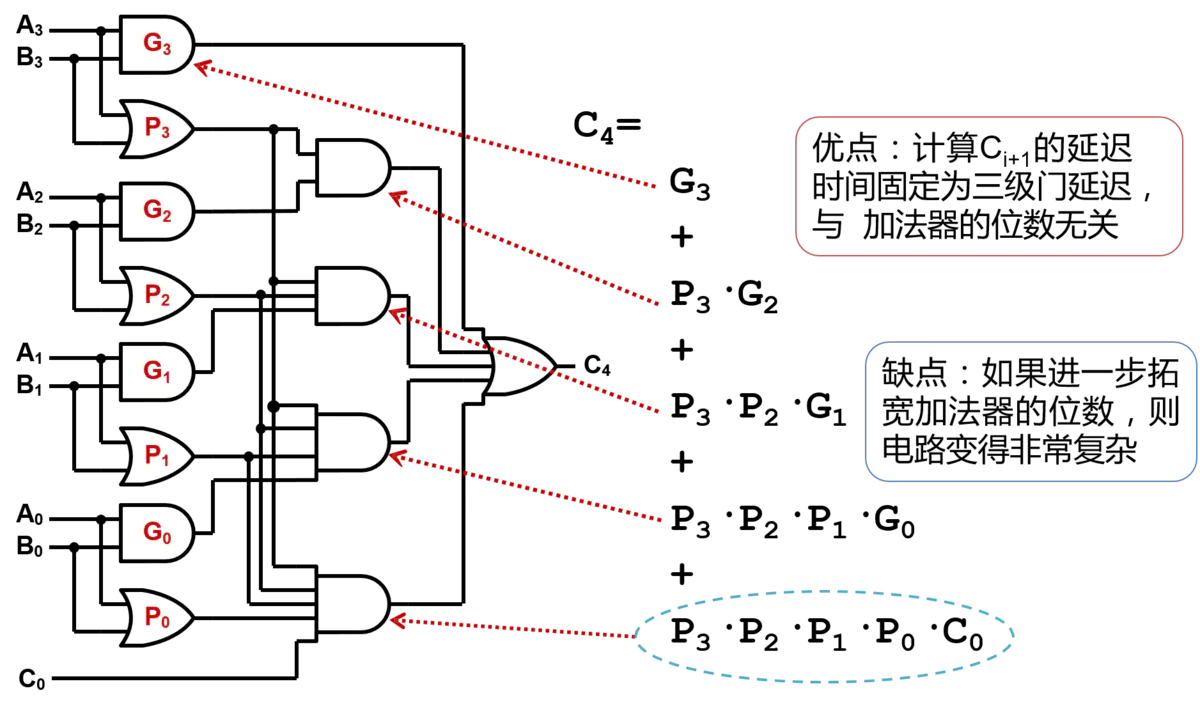
工作原理:鉴于波纹进位加法器需要等待前一位的进位结果(
观察某一位的
则通过上述分析可以得出:
将上述结果进行不断套娃,可以直接得到更高位的结果直接以外部变量表示的表达式。
以16位的超前进位加法器为例,其可以被分为四个子模块,然后再将其串起来,得到以下结构:
每一个子结构又如下所示:
进位跳过加法器是一种在面对最坏情况时较为快捷的处理进位的方法,其将整个
根据理论表明,当每一个小块的位宽为
注:$t_{sum}$ 为一位加法器得到本位结果的时间,也就是两个异或门的时间;
上述结果通过数学知识可得,当
进位选择加法器的原理也是将固定位数的加法运算分成更小的”块“,并在块中运用两个加法器分别计算进位分别是1、0的结果,最后由二选一复用器决定采用什么作为最后的结果。不同的是,该加法器的最终结构是将该方法不断递归运行下去,最后得到的时间损耗仅仅是做单个加法运算的
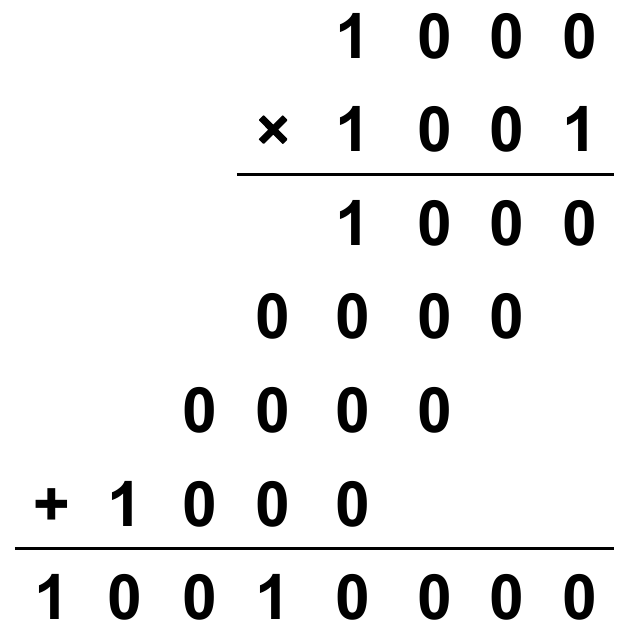
与我们使用竖式计算十进制乘法相同,我们也可以使用竖式计算二进制乘法,如下图是一个使用竖式计算二进制乘法 $1000 \times 1001 $ 的例子:
我们将1000称为 multiplicand(被乘数) ,将1001称为 multiplier(乘数)。
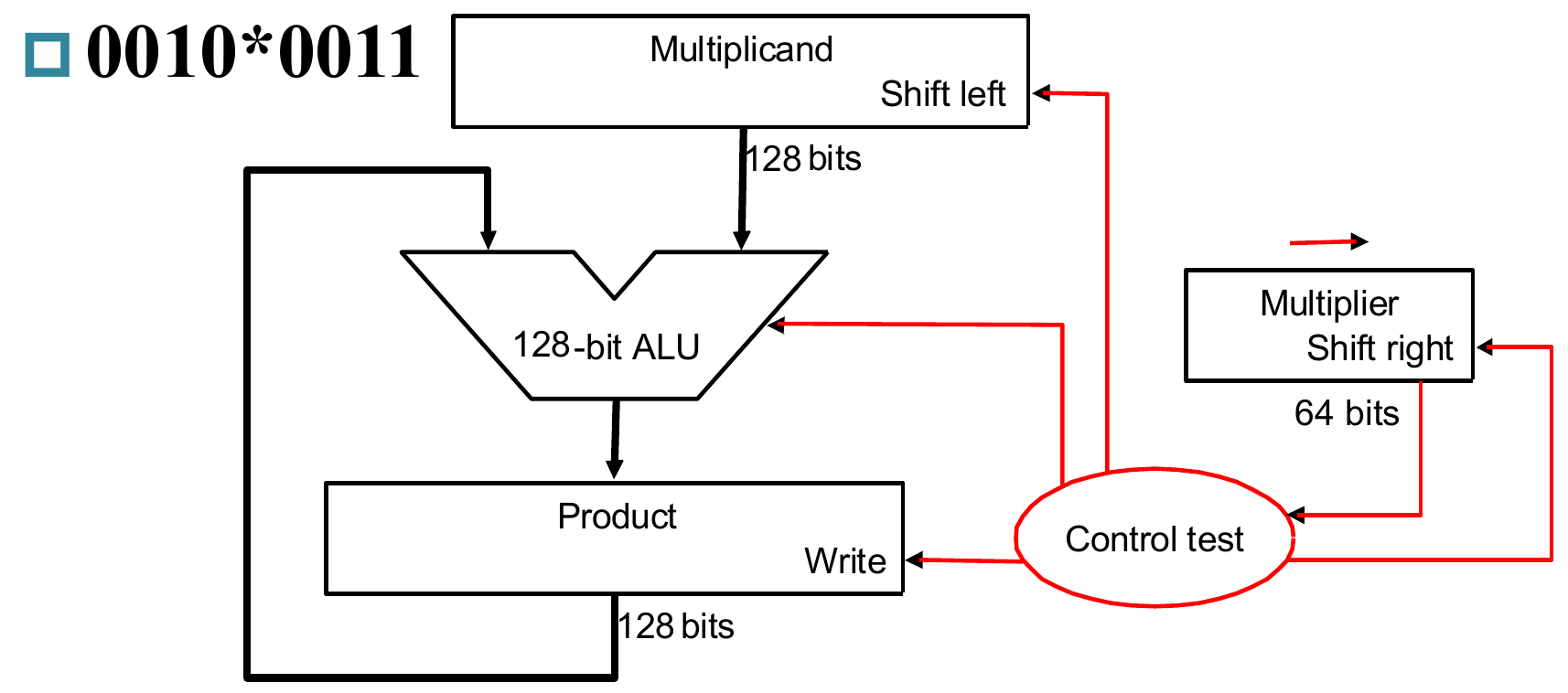
1.检测乘数最低位是否为1?如果是1,则将结果寄存器加被乘数,将结果返回至结果寄存器。
2.将被乘数整体左移一位、乘数整体右移一位。
3.判断是否已经移位64次(以64位乘法为例)。如果是,则运算结束、输出结果;否则继续循环。
所需两个128位寄存器和一个64位寄存器、128位ALU;
需要进行64次迭代,近200次循环。
时间和空间都有过多浪费!
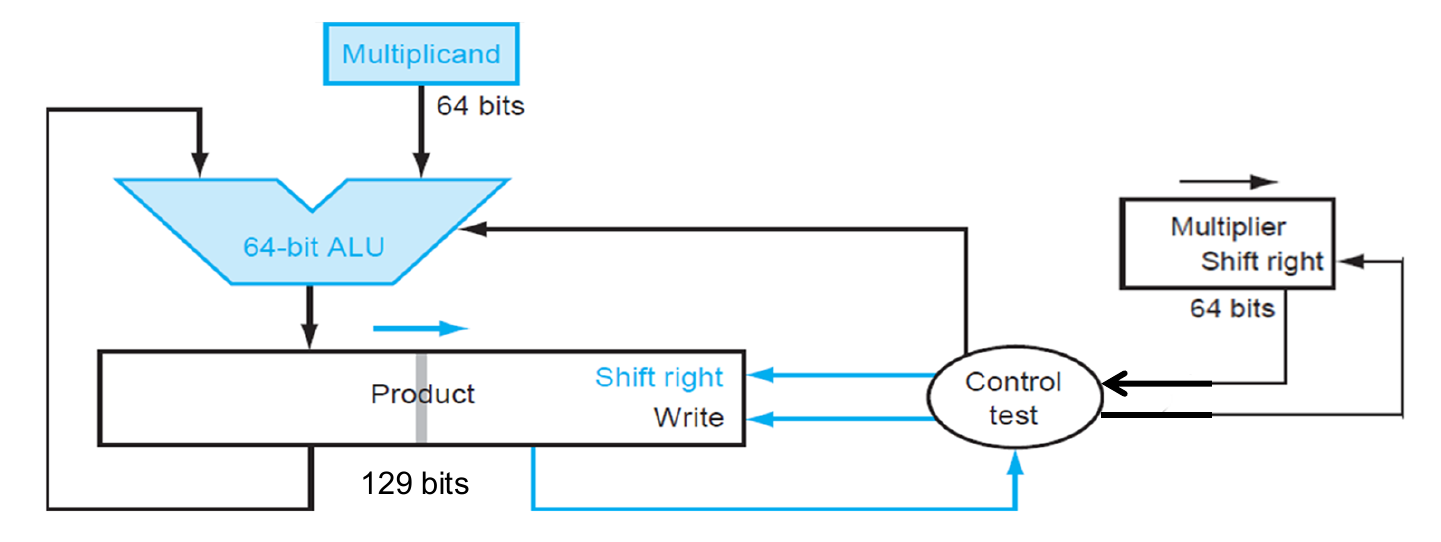
通过竖式计算我们可以看到:实际的运算只有64位,而128位只是产生的移位而已。因此我们想到,可以不将被乘数扩展为128位(不移位被乘数),仅移位乘积结果和乘数。这样的好处是可以将被乘数寄存器和ALU都降低为64位。
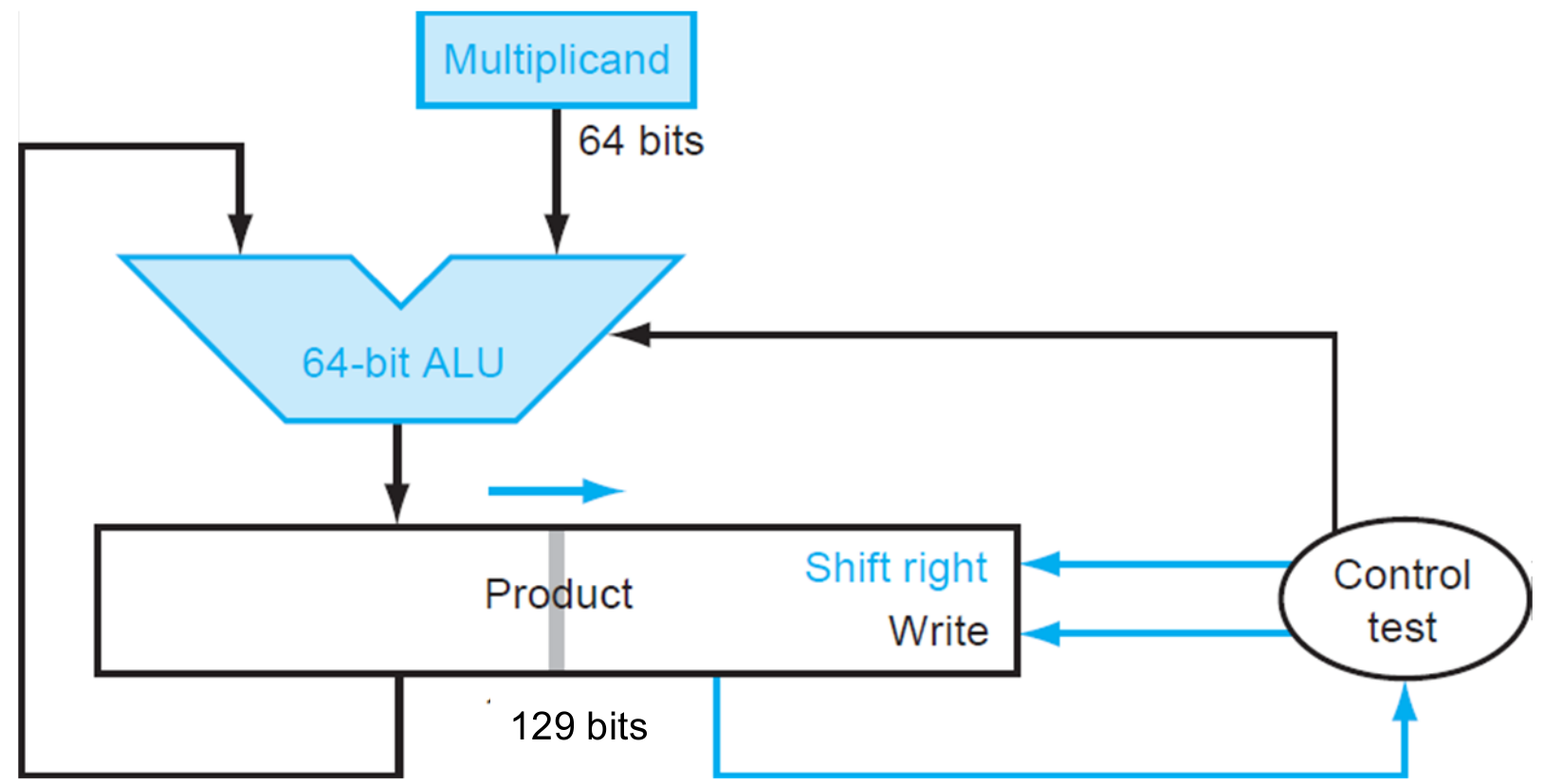
1.判断乘数最低位是否为1?如果是1,则将 结果寄存器的前64位与被乘数相加,将结果返回至结果寄存器中。
2.将结果和乘数都右移一位,
3.是否重复了64次?如果是,则输出结果寄存器的结果;否则继续循环。
请注意:结果寄存器是129位的,因为需要考虑移位时产生的进位现象。若没有左侧额外的一位,进位将无处保存!
所需两个64位寄存器、一个129位寄存器和一个64位的ALU,相比V-1.0大幅下降
时间和V-1.0相似
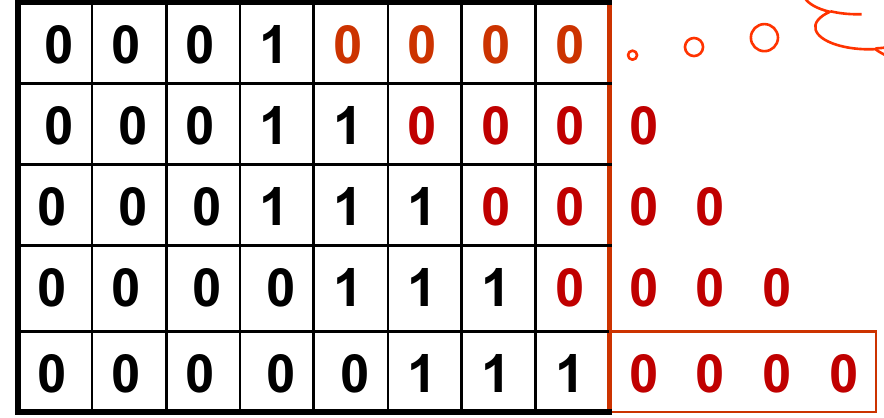
观察V-2.0所使用的129位的结果寄存器,可以发现:后边的64位一开始均为0,这些空间实际上被浪费掉了。如下图:
再联想到 每次我们只需要乘数的最末位,且使用过的位会被扔掉 ,我们想到,可以将 乘数放在结果寄存器的低位64位来节省空间 。
只需在V-2.0的基础上将乘数储存在结果寄存器的低位64位即可。
仅有一个64位寄存器、129位寄存器和64位ALU,最大限度地节省了空间和时间。
最基本的思路是:将其转化为无符号数的运算:
1.存储运算数的符号位
2.将有符号数转化为无符号数(使
3.进行乘法运算
4.将两个数的符号位进行异或操作以决定最终得数的符号位
但可以发现,这样的操作耗时耗力,还需要额外的电路模块,下面对其进行改进。
在面对一个运算数含有多个连续的”1“时,我们在上述V-3.0乘法模块中需要进行多次加法,但能不能将其简化为次数较少的加减法与多次移位相结合呢?比如,我们有如下一个例子(二进制):
而我们其实省略了中间的:
根据V-3.0所得,这些被省略的”0“只需要进行移位即可,无需在ALU中进行计算,这样就为我们对有符号数计算的简化提供了思路。
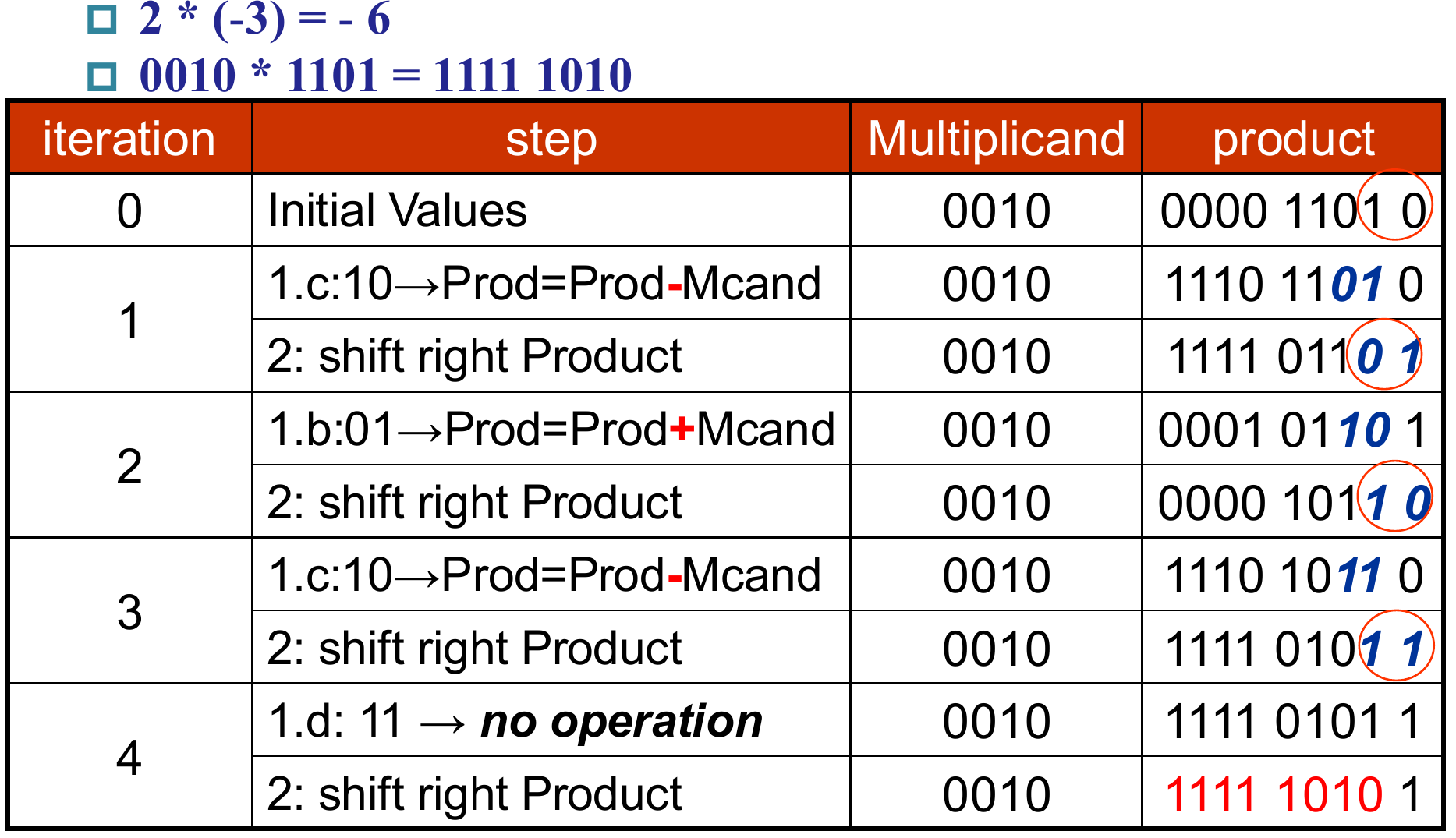
1.运算过程仍包含
2.(以64位乘法相乘为例)初始结果寄存器由前64位”0“、复制乘数的64位和最右侧被添加的”0“组成
3.每次比较结果寄存器最低的两位,所作操作如下表所示:
| 最低两位的组成 | 所进行操作 |
|---|---|
| 0 0 | 不进行任何操作,将整个结果寄存器 算术右移 |
| 1 1 | 不进行任何操作,将整个结果寄存器 算术右移 |
| 1 0 | 最高的64位减去被乘数,将整个结果寄存器 算术右移 |
| 0 1 | 最高的64位加上被乘数,将整个结果寄存器 算术右移 |
注:算术右移(arithmetic shift right)指的是右移一位,并将右移前的最高位的值赋给右移后的最高位(以保证该数的正负一致),而逻辑右移(logical shift right)则是右移后直接在最高位补”0“,具体区别请看下表:
| 右移类型 | 四位”1101“的变化 | 四位”0101“的变化 |
|---|---|---|
| 算术右移(arithmetic shift right) | 1110 | 0010 |
| 逻辑右移(logical shift right) | 0110 | 0010 |
4.重复上述操作直至
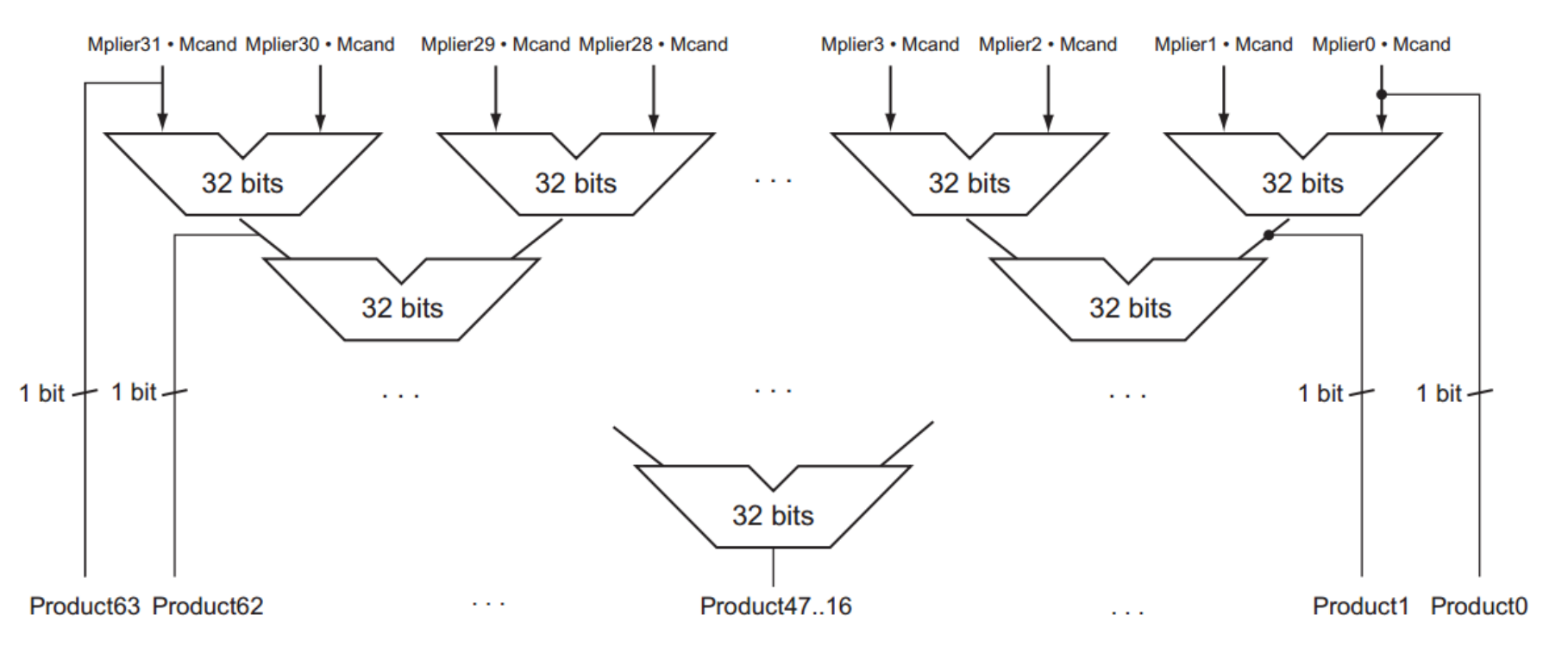
无论是以上哪个版本的乘法模块,都要经过64次串行循环,极大地浪费了时间。因此人们考虑能不能不进行如此循环,而是通过增大电路成本压缩运算时间:
这一设计强调了:
1.Follow the Moore's Law。
2.Performance via Pipelining。
可以通过该指令判断64位的溢出
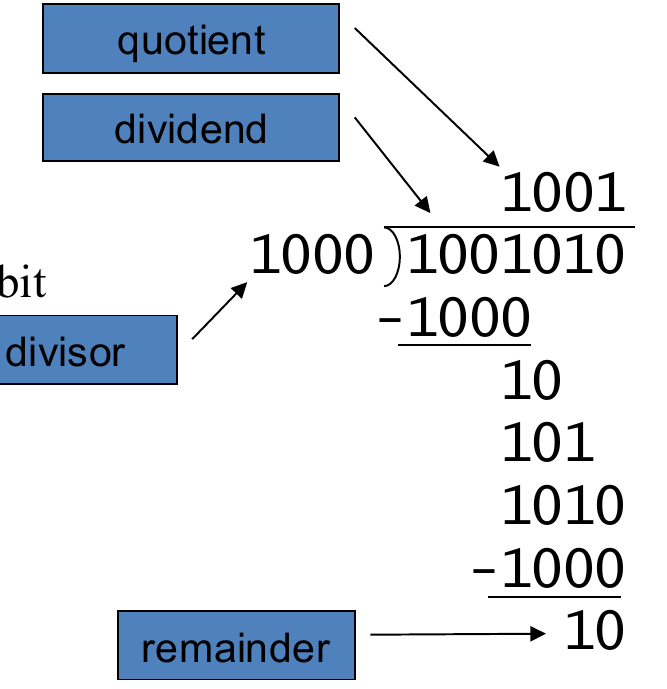
在日常运算中,我们进行除法运算时通常采用的是长除法,即下图的例子:
在二进制除法的构建中,我们也会模拟这样的步骤:
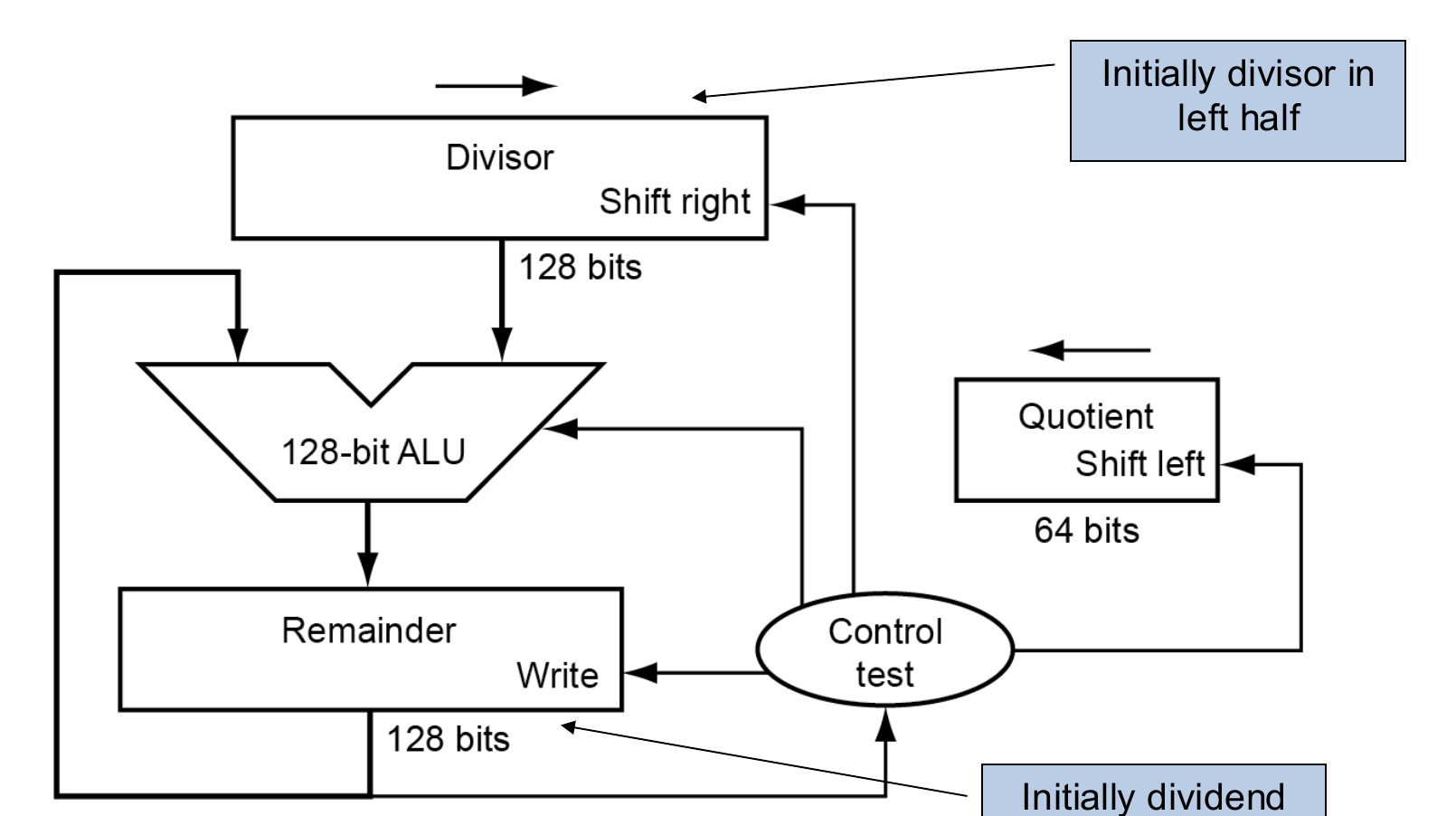
1.检查除数是否为0,若为0,则溢出并返回一个特定的值;否则将除数储存在除数寄存器的高位上。将被除数储存在余数寄存器的低位中。
2.进行长除:将余数寄存器中的被除数减去除数寄存器的值并储存在余数寄存器中,如果结果大于0,则此位的商为1,保留减法得到的结果;如果结果小于0,则此位的商为0,将被除数还原(加上除数)
3.除数右移一位,继续进行循环,直至做了65(
本模块使用了两个128位寄存器分别作为被除数和除数,一个64位寄存器用于存储商的结果,一个128位ALU用于处理被除数与除数之间的减法运算。就像乘法的V-1.0版本一样,该设计仍然消耗了过多的空间。
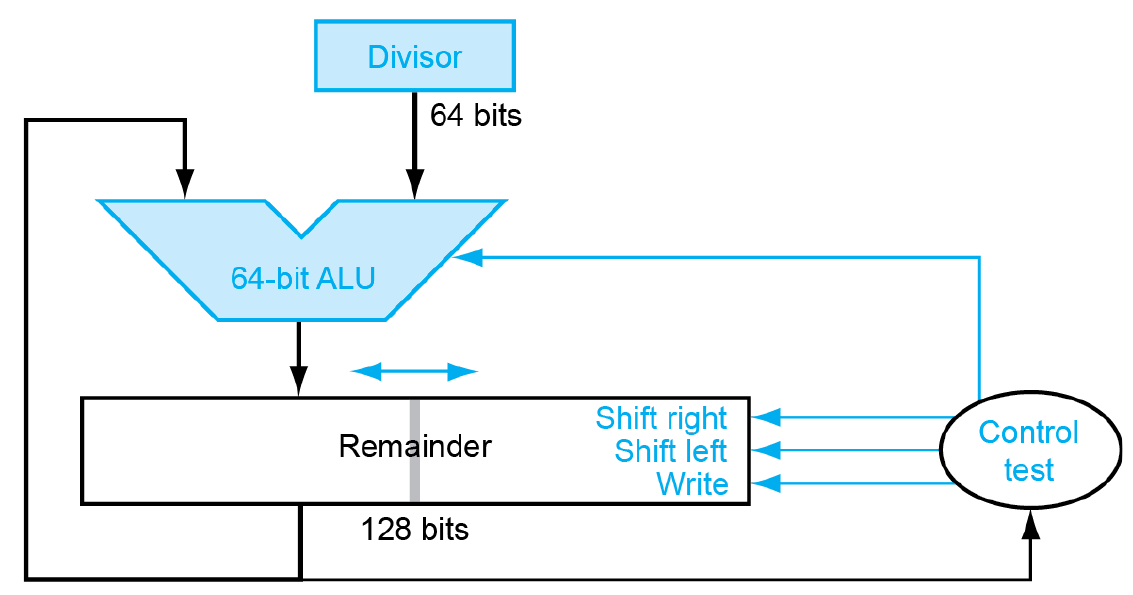
在V-1.0中我们通过“扩充”除数来达到长除的目的,但这样既浪费了一定的空间,还让ALU从
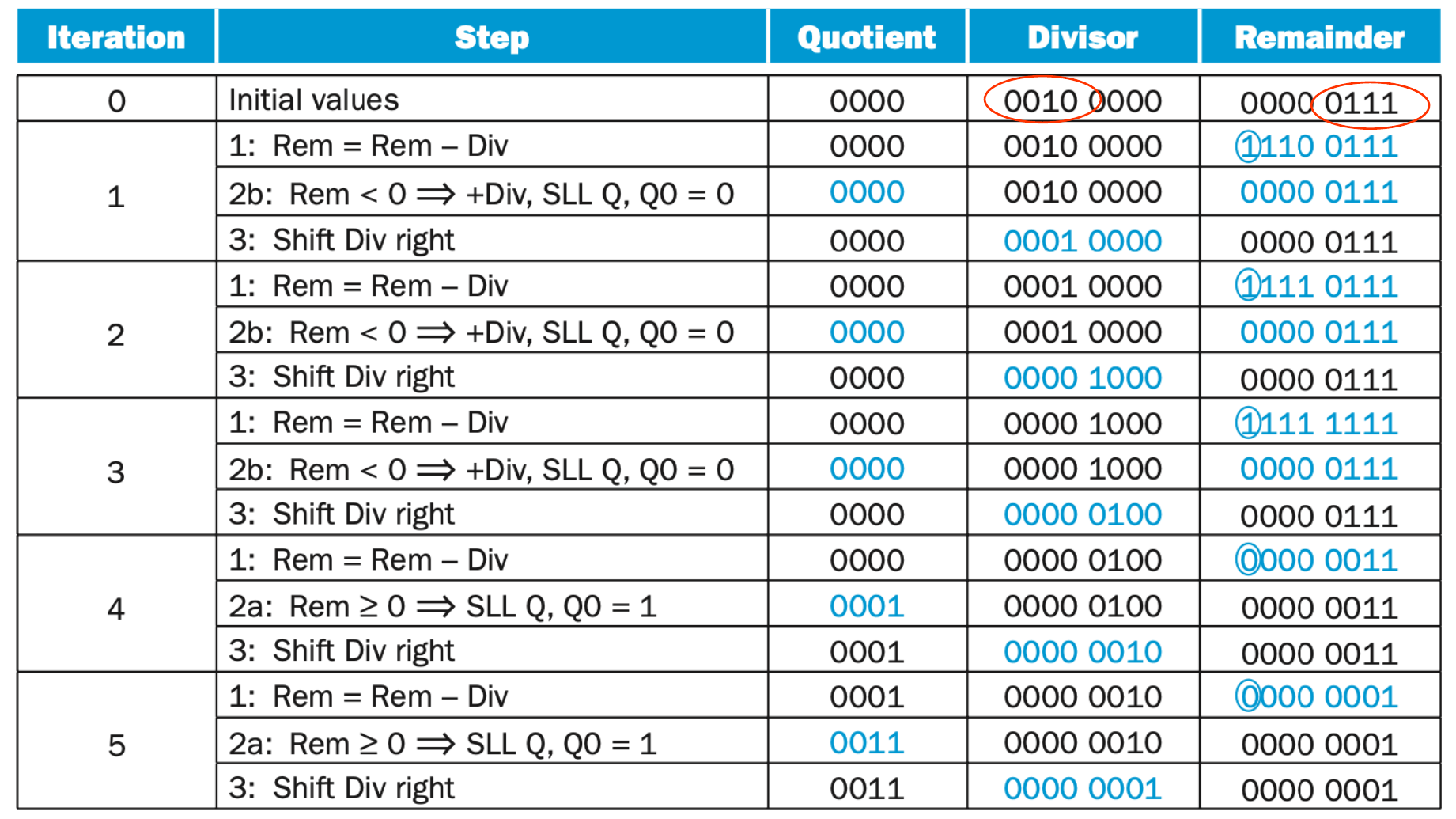
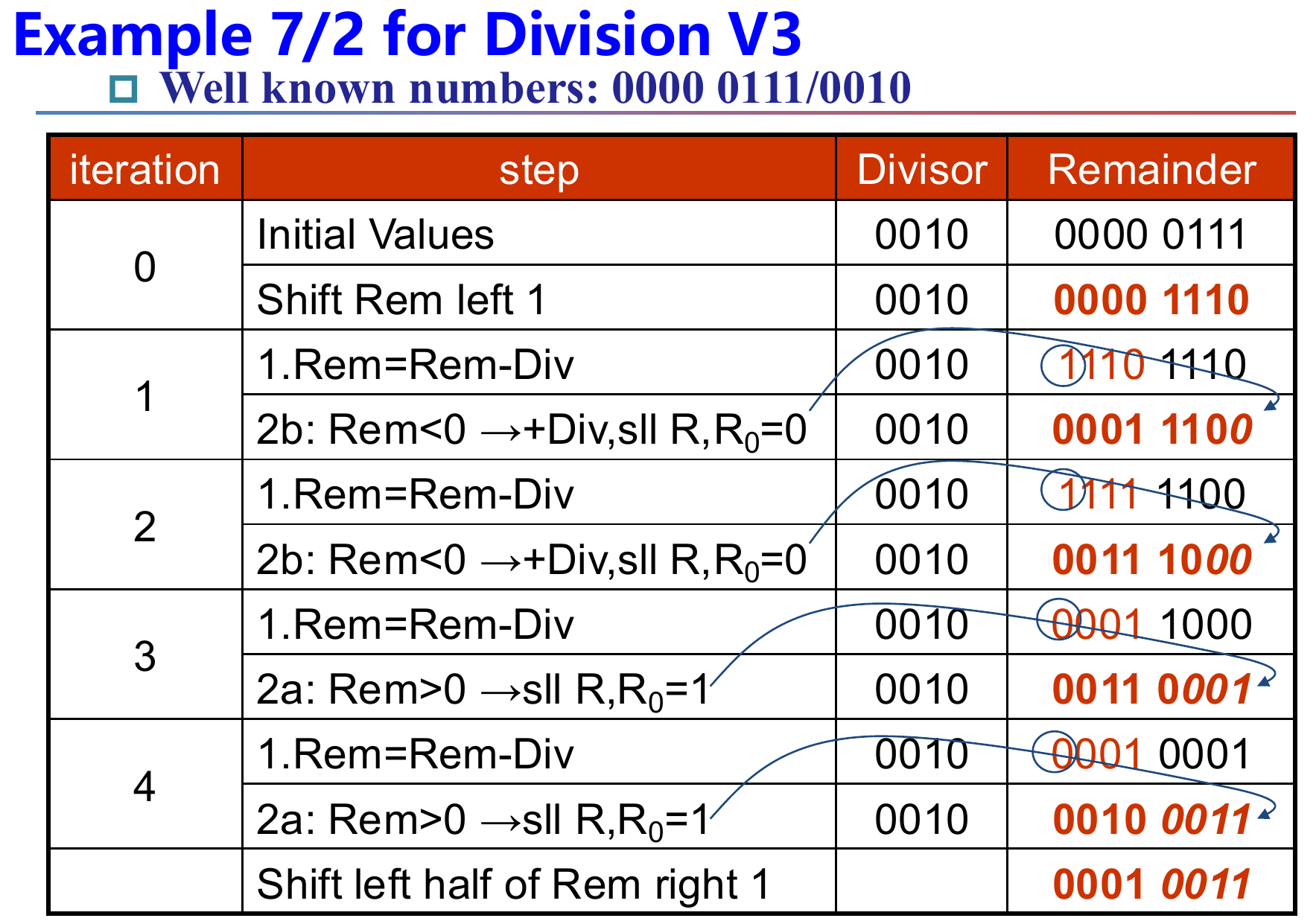
1.首先将被除数输入为余数寄存器的64位低位,高位全部置0。逻辑左移余数寄存器一位(右端补0)。
2.余数寄存器64位高位减去除数,判断结果是否大于0(可直接通过最高位判断):若结果大于0,则逻辑左移余数寄存器,再+1(将最低位由0变为1);若结果小于0,则将余数寄存器64位高位复原并逻辑左移余数寄存器。
3.重复第二步直至进行64次循环为止。
4.将余数寄存器64位高位逻辑右移1位。余数寄存器的64位高位即为结果的余数;64位低位即为结果的商。
这个版本的除法模块在最大限度地节省了空间的同时,将ALU也设法减负到了最低水平。
在寄存器记忆被除数和除数的符号之后,余数和商的符号也就确定了下来:余数符号与被除数相同,商的符号为两符号异或的结果:被除数和除数符号相同,商的符号为正,否则为负。
div,rem:signed divide, remainder
divu,remu:unsigned divide, reminder
这两个寄存器属于协处理器,一般不在通用寄存器的范围内,用于处理乘除操作。能够协助中央处理器完成一些其无法完成或效率低下的任务。
随着芯片技术的发展,乘除、浮点数运算等都已集成于中央处理器内,PC已经不再有协处理器。
根据摩尔定律,我们可以通过优化硬件的方式提高运算速度。但我们没有办法像并行计算乘法那样并行计算除法。但我们有更好的办法通过预测提高运算速度。例如SRT算法:SRT除法的一些理解 - 知乎 (zhihu.com)
我们在使用科学计数法来规范化表示一个数时,会规定其小数点的位置(必须在从左往右数第一个数字后)。例如:
其中,
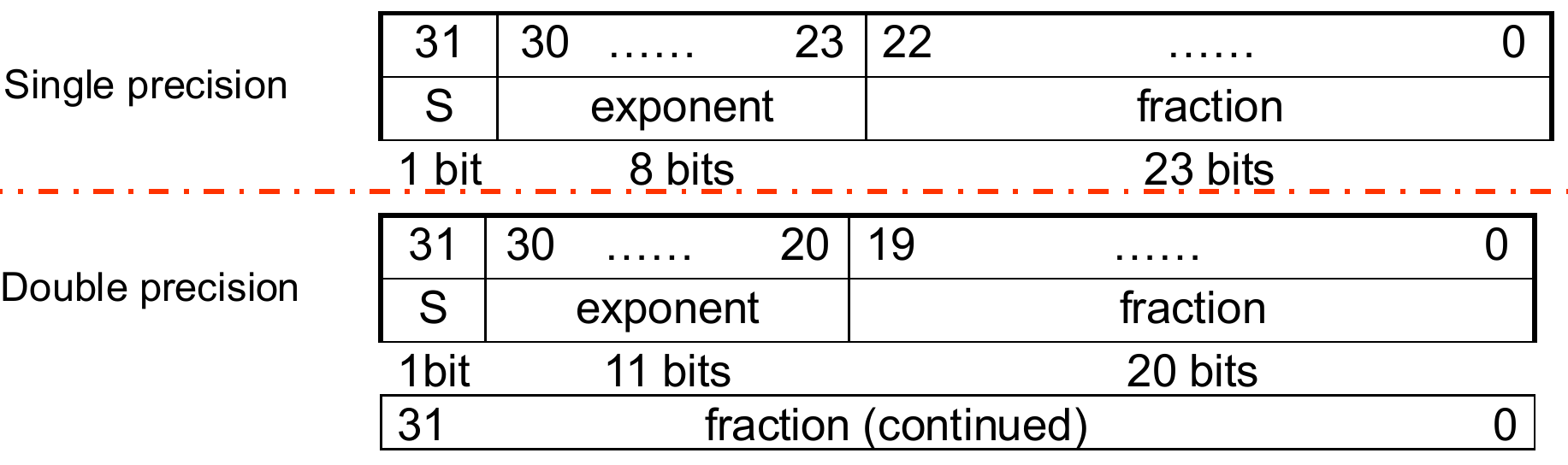
单精度浮点数由32位组成,双精度浮点数由64位组成。
符号位仅在最高位占一位,0表示正数,1表示负数。
由于阶码有正有负,因此阶码由移码表示,也就是说其有一定的偏移量(bias)。实际的阶码值应由阶码的纸面值减去偏移值。不同的浮点数对应偏移值也不同:
| Type | Bias |
|---|---|
| Single precision(单精度) | 127 |
| Double precision (双精度) | 1023 |
注意:虽然最小和最大的阶码分别是000...000和111...111。但在计算正常浮点数阶码范围时,正常情况下不使用000...000—111...111而使用000...001—111...110作为其范围,因为首位两个数在表示时有其独特的应用。
尾数码使用原码表示,即所见即所得。也就是标准规范中的
单精度浮点数:
根据单精度浮点数1位符号位,8位阶码,23位尾数码,对其进行分割:
红色的符号位1表示这是一个负数;绿色的阶码1000001是移位表示,需要转为真值。也就是
最小的阶码为00000001,真值为
最大的阶码为11111110,真值为
同理可得,双精度浮点数的最小值、最大值分别为:
浮点数所有的尾数码都有其意义和表示,因此需要从尾数码找到其能表示的最低精确数字。
单精度浮点数能表示到约
双精度浮点数能表示到约
阶码全为1、尾数码全为0:
阶码全为1、尾数码不全为0:
阶码全为0,此时浮点数的表示为非规格化数,此时尾数码将不再有隐含的1.0。可用于表示非常接近0的小数。
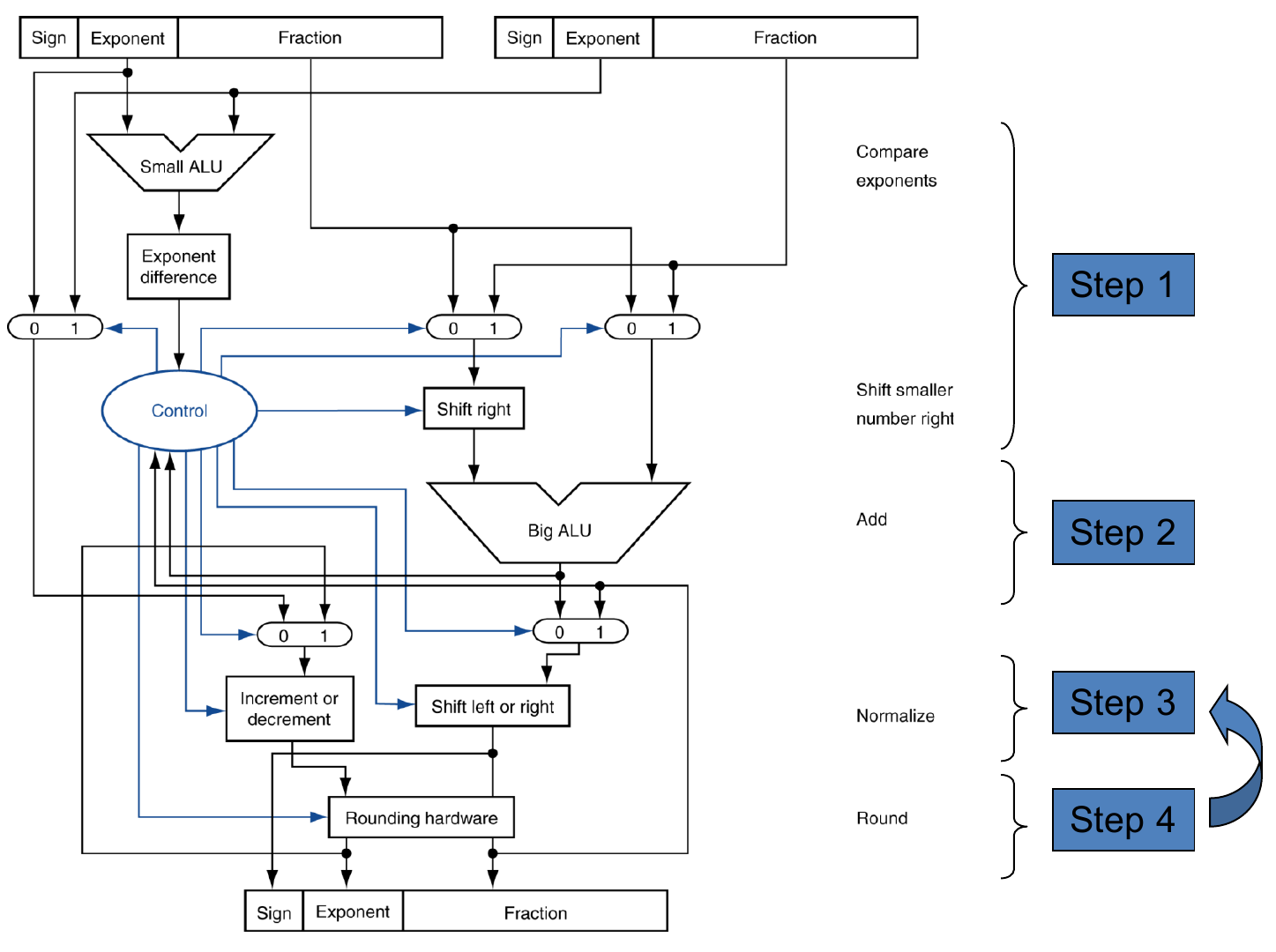
1.Alignment(对齐):将两个浮点数的阶码进行比较,将较大的阶码作为最后结果的阶码,并对阶码较小的浮点数进行对齐(阶码每递增1,尾数码就要对应逻辑右移一位)
2.Addition of significands:将已经对齐好的两浮点数的尾数码相加,得到一个结果。(当然此时的相加减需要考虑到两个数的符号)
3.Normalisation of the result:上述的结果未必符合浮点数表示的正确规范,因此要结合尾数码和阶码对结果进行调整(正如我们十进制的科学计数法需要调整小数点的位置一样)
4.Rounding(舍入):对结果进行舍入的调整,具体的四种舍入方法将会在后文给出。
具体分析:左上半部分是我们所说的比对对齐操作,通过一个小型(只支持减法)的ALU来判断两个浮点数的阶码大小及差距并将结果返回至控制中心,控制中心再反过来根据结果控制尾数码的右移。在右移之后,尾数码便能进行真正的加减法(与符号位有关),并在后续执行Normalize和Round过程。
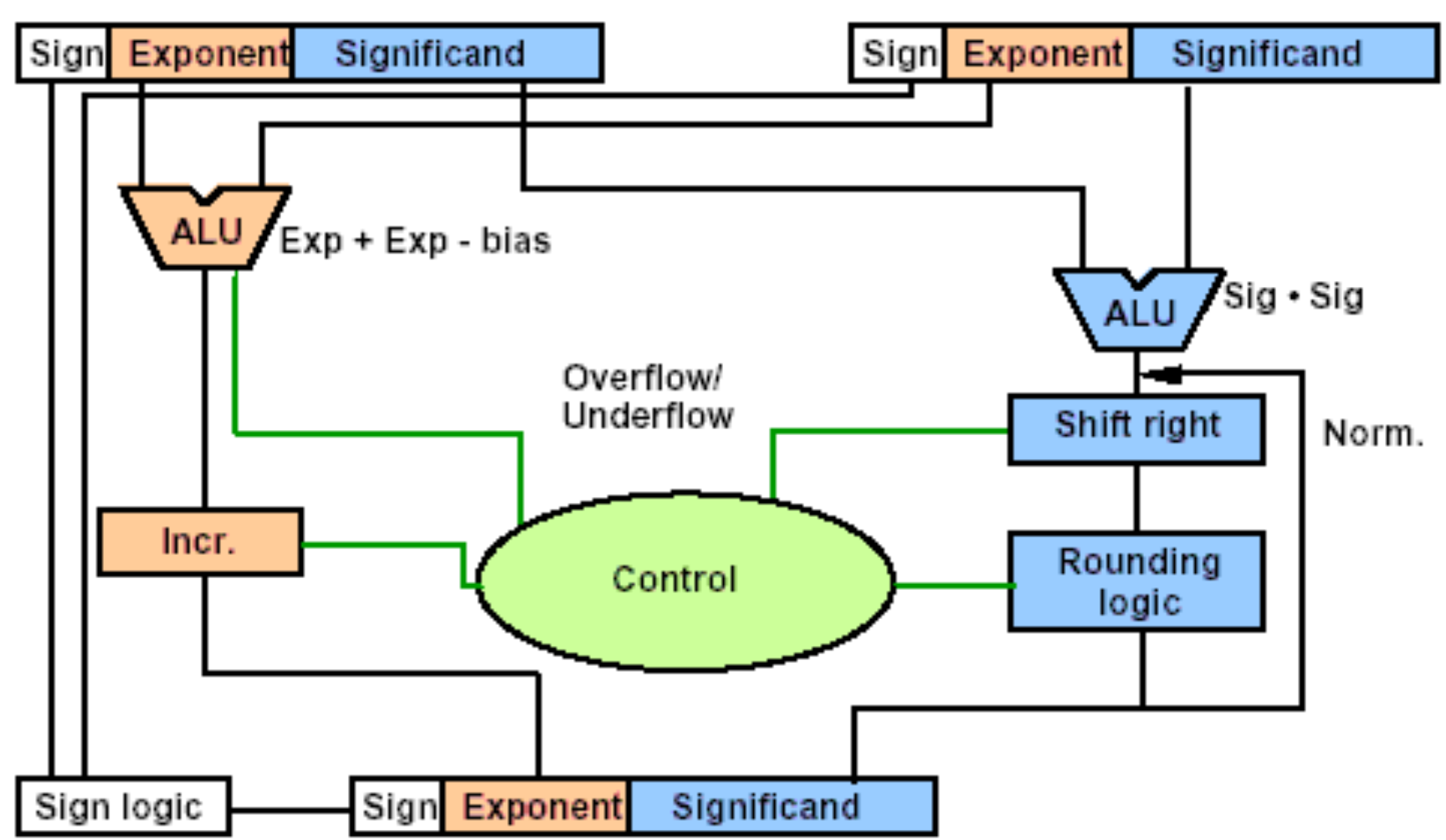
除法与乘法步骤几乎相同。
1.阶码相减
2.尾数码相除
3.Normalisation
4.Rounding
5.Sign
以下面的运算为例:
如果最终只有三位有效位,则需要进行取舍:
Guard位:有效位的低一位,也就是本例中的“5”。
Round位:在英文中这既代表“Round”这一过程,同时也可表示Guard位的低一位,也就是本例中的6.
Sticky位:只要在Round位的更低位中有非0的存在即为1(用于在某些特定情况下判断是否恰好在两精确数的中间)
units in the last place(ulp):偏移比例,前后相加必为1.例如:若浮点数可以精确表示2.33和2.38,则对2.35的表示中,2.33的ulp即为0.4ulp,2.38即为0.6ulp。
以最接近且大于的数替代
以最接近且不大于的数替代
直接将有效位之外的位截断
1.寻找ulp最小的数替代
2.如果出现ulp均为0.5的情况:
总是使最低有效位(LSB)为0(如下图)