在概率论中,卷积表示成这样
连续型
离散型
并且也解释了,先对g函数进行翻转,相当于在数轴上把g函数从右边褶到左边去,也就是卷积的“卷”的由来。
然后再把g函数平移到n,在这个位置对两个函数的对应点相乘,然后相加,这个过程是卷积的“积”的过程。
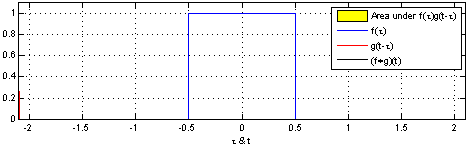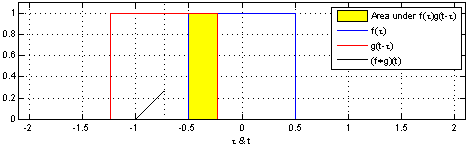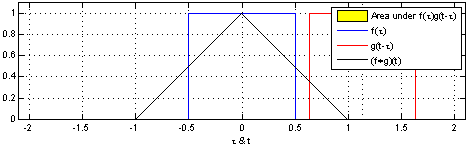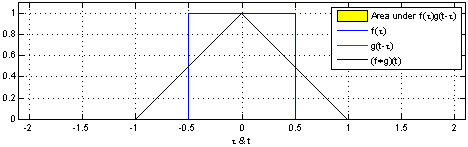
下图很好地表示了卷积的过程
在图像处理中,同样需要卷积来减小运算量。
现在一个图片动则几MB,考虑三种颜色,参数可能至少上百万,单个图片就如此高,那么多个图片更不用想了。
于是我们通过卷积来减小运算量。
具体的,如下图,我们定义一些卷积核函数,这些函数能表示图像中的特征,且可以通过组合卷积核来拼凑出完整的图像。
我们将卷积核逐个上面原始图片,将卷积后的值作为卷积后特征
可以看出,卷积后的结果没有减少太多资源,因为只有n-1行(列)被消除了
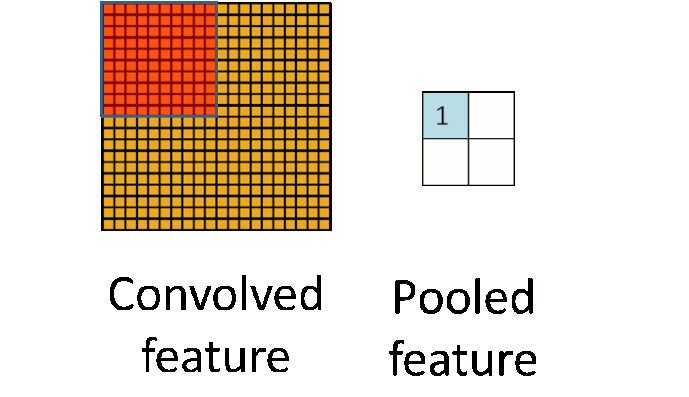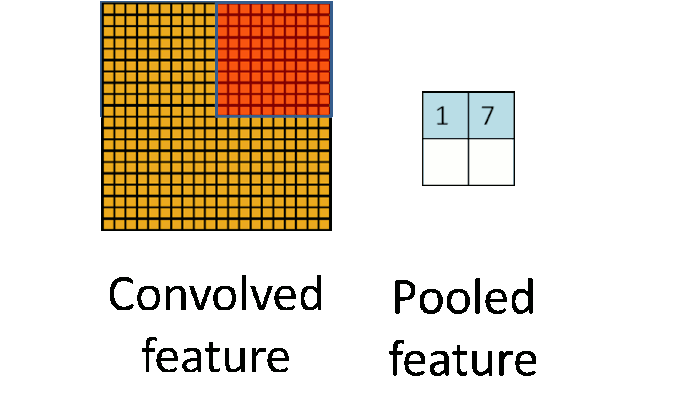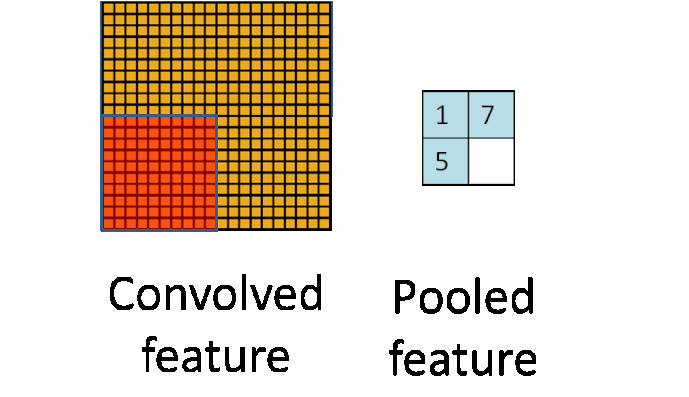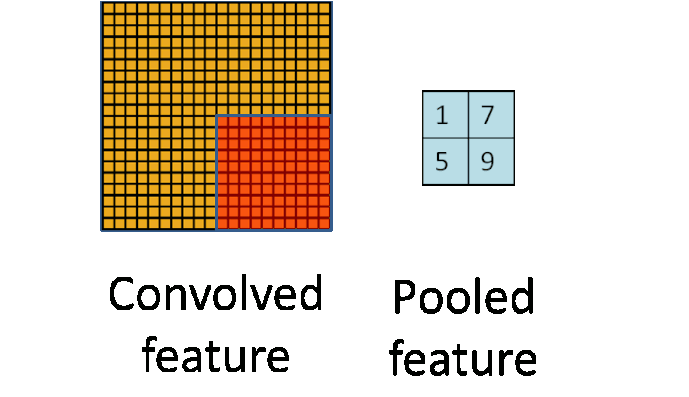
我们可以考虑将卷积后的结果降维,最简单的当然是分成几块各自运算没有重复。
这个部分就是最后一步了,经过卷积层和池化层处理过的数据输入到全连接层,得到最终想要的结果。
经过卷积层和池化层降维过的数据,全连接层才能”跑得动”,不然数据量太大,计算成本高,效率低下,还会出现过拟合。