-
Notifications
You must be signed in to change notification settings - Fork 3
/
P7_rasterPackageAdvanced_I-v1.Rmd
437 lines (297 loc) · 19.9 KB
/
P7_rasterPackageAdvanced_I-v1.Rmd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
---
title: "P7 – Advanced techniques with raster data (part-1) - Unsupervised Classification"
author: "Joao Goncalves"
date: "25 November 2017"
output:
html_document:
self_contained: no
pdf_document: default
---
```{r setup, include=FALSE}
knitr::opts_chunk$set(echo = TRUE)
knitr::opts_chunk$set(fig.path = "img/")
knitr::opts_chunk$set(fig.width = 5, fig.height = 4.5, dpi = 80)
```
### Background
-------------------------------------------------------------------------------------------------------
The process of _unsupervised classification_ (UC; also commonly known as _clustering_) uses the properties and
moments of the statistical distribution of pixels within a feature space (e.g., formed by different spectral
bands) to differentiate between relatively similar groups. _Unsupervised classification_ provides an
effective way of partitioning remotely-sensed imagery in a multispectral feature space and extracting useful
land-cover information. We can perhaps differentiate UC from clustering because the first implies that we
investigate _a posteriori_ the results and, label each class accordingly to its properties. For example, if
the objective is to obtain a land cover map, then different groups will perhaps be differentiated and labeled
into urban, agriculture, forest and other classes alike.
Clustering is also known as a _data reduction_ technique, i.e. it compresses highly diverse information at
pixel-level into groups or clusters of pixels with similar and more homogeneous values. Contrarily to
_supervised classification_ , the _unsupervised_ version does not require the user to
provide training samples or cases. In fact, UC needs minimal inputs from the operator and typically only the
definition of the number of groups and which bands to use are given. Then the algorithm attempts to provide
the best solution to cluster pixel values such that _'within-group'_ distances are minimized and _'between-groups'_
separation is maximized.
In this post we will explore how to:
* Perform unsupervised classification / clustering,
* Compare the performance of different clustering algorithms, and,
* Assess the _"best"_ number of clusters/groups to capture the data.
One satellite scene from [Landsat 8](https://landsat.gsfc.nasa.gov/landsat-8/landsat-8-bands/)
will be used for this purpose. The data contains [surface reflectance](http://glcf.umd.edu/data/gls_SR/)
information for seven spectral bands (or layers, following the terminology for `RasterStack` objects)
in GeoTIFF file format.
The following table summarizes info on Landsat 8 spectral bands used in this tutorial.
Band # | Band name | Wavelength (micrometers)
-------- | ------------------------------ | -------------------------
Band 1 | Ultra Blue | 0.435 - 0.451
Band 2 | Blue | 0.452 - 0.512
Band 3 | Green | 0.533 - 0.590
Band 4 | Red | 0.636 - 0.673
Band 5 | Near Infrared (NIR) | 0.851 - 0.879
Band 6 | Shortwave Infrared (SWIR) 1 | 1.566 - 1.651
Band 7 | Shortwave Infrared (SWIR) 2 | 2.107 - 2.294
Landsat 8 spatial resolution (or pixel size) is equal to 30 meters. Valid reflectance decimal values
are typically within 0.00 - 1.00 but, for decreasing file size, the valid range is multiplied
by a 10^4^ scaling factor to be in integer range 0 - 10000. Image acquisition date is the 15^th^ of July 2015.
For more information on raster data processing see [here](http://r-exercises.com/tags/raster-data), as well as the [tutorial part-1](https://www.r-exercises.com/2017/11/29/spatial-data-analysis-introduction-to-raster-processing-part-1), [tutorial part-2](https://www.r-exercises.com/2017/12/13/spatial-data-analysis-introduction-to-raster-processing-part-2), [tutorial part-3](https://www.r-exercises.com/2018/01/10/spatial-data-analysis-introduction-to-raster-processing-part-3), and, [tutorial part-4](https://www.r-exercises.com/2018/01/24/spatial-data-analysis-introduction-to-raster-processing-part-4) of this
series.
### Unsupervised classification / clustering
-------------------------------------------------------------------------------------------------------
For performing the unsupervised classification / clustering we will employ and compare two algorithms:
- __K-means__, and,
- __CLARA__
#### K-means algorithm
The _k-means_ clustering algorithm attempts to define the centroid of each cluster with its mean value.
This means that data are partitioned into _k_ clusters in which each observation belongs to the cluster
with the nearest mean, serving as a prototype of the cluster. In a geometric interpretation, k-means
partitions the data space into _Voronoi cells_ (see plot below). K-means provides an "exclusive" solution,
meaning that each observation belongs to one (and only one) cluster. The algorithm is generally efficient
for dealing with large dataset which commonly happens for raster data (e.g., satellite or aerial images).

#### CLARA algorithm
The CLARA (Clustering LARge Application) algorithm is based on the Partition Around Medoids (PAM) algorithm
which in turn is an implementation of K-medoids... `r emo::ji("worried")`... so let's try to dig in by parts.
Also, since these posts are intended to be _'short-and-sweet'_, I will not use mathematical notation
nor pseudocode in descriptions. There are plenty of awesome books and online resources on these subjects
that can be consulted for more information.
The _k-medoids_ algorithm is a clustering algorithm similar to k-means. Both are _partitional_ algorithms
in the sense that they break-up up the data into groups and both attempt to minimize the distance between
points labeled in a cluster and a point designated as the center of that cluster.
However, in contrast to the k-means algorithm, k-medoids chooses specific data-points as centers (named as _medoids_)
and works with a generalization of the Manhattan Norm to define the distance between data-points. A medoid
can be defined as the object of a cluster whose average dissimilarity to all the objects in the
cluster is minimal. i.e., it is a most centrally located point in the cluster.
Generally, k-medoids is more robust to noise and outliers as compared to k-means because it minimizes
a sum of pairwise dissimilarities instead of a sum of squared Euclidean distances.
_PAM_, is the most common realization of the k-medoids clustering algorithm. PAM uses a greedy search which
may not find the optimum solution, however it is faster than a exhaustive search. PAM has a high computational
cost and uses a large amount of memory to compute the dissimilarity object. This leads us to the _CLARA_ algorithm!
_CLARA_ randomly chooses a small portion of the actual data as a representative of the data and then medoids are
chosen from this sample using _PAM_. If the sample is robustly selected, in a fairly random manner and with
enough data-points, it should closely represent the original dataset.
_CLARA_ draws multiple samples of the dataset, applies PAM to each sample, finds the medoids, and then returns
its best clustering as the output. At first, a sample dataset is drawn from the original dataset and the
PAM algorithm is applied to find the _k_ medoids. Using these _k_ medoids and the whole dataset, the 'current'
dissimilarity is calculated. If it is smaller than the one you get in the previous iteration, then these
_k_ medoids are kept as the best ones. This process of selection is iteratevely repeated a specified
number of times.
In R, the `clara` function from the `cluster` package implements this algorithm. It accepts
dissimilarities calculated based on `"euclidean"` or `"manhattan"` distance. Euclidean distances
are root sum-of-squares of differences while Manhattan distances are the sum of absolute
differences.
#### Workflow
Our approach to clustering the Landsat 8 spectral raster data will employ two stages:
(i) Cluster image data with _K-means_ and _CLARA_ for a _number of clusters_ between 2 and 12;
(ii) Assess each clustering solution performance through the average _Silhouette Index_.
Let's start by downloading and uncompressing the Landsat-8 surface reflectance sample data for
the Peneda-Geres National Park:
```{r P7_download_data, eval=FALSE, echo=TRUE, message=FALSE, warning=FALSE}
## Create a folder named data-raw inside the working directory to place downloaded data
if(!dir.exists("./data-raw")) dir.create("./data-raw")
## If you run into download problems try changing: method = "wget"
download.file("https://raw.githubusercontent.com/joaofgoncalves/R_exercises_raster_tutorial/master/data/LT8_PNPG_MultiBand.zip", "./data-raw/LT8_PNPG_MultiBand.zip", method = "auto")
## Uncompress the zip file
unzip("./data-raw/LT8_PNPG_MultiBand.zip", exdir = "./data-raw")
```
Now, let's read the multi-band GeoTIFF file into R as a `RasterBrick` object:
```{r P7_load_data_into_r, message=FALSE, warning=FALSE}
library(raster)
# Load the multi-band GeoTIFF file with brick function
rst <- brick("./data-raw/LC82040312015193LGN00_sr_b_1_7.tif")
# Change band names
names(rst) <- paste("b",1:7,sep="")
```
Plot the data in RGB display (bands 4,3,2) to see if everything is fine:
```{r P7_plot_rgb_LT8, fig.height=5, fig.width=5, eval=FALSE, echo=TRUE}
plotRGB(rst, r=4, g=3, b=2, scale=10000, stretch="lin", main="RGB composite (b4,b3,b2) of Landsat-8")
```

Data is OK which means we can proceed with _step #1_, i.e. clustering raster data with both algorithms
and for different numbers of clusters (from 2 to 12).
For simplifying the processing workflow, the 'internal' values of the raster object will be entirely load up
into memory into a `data.frame` object (in this case with `r ncell(rst)` rows - one for
each cell; and, `r nbands(rst)` columns - one for each layer; see also `?values` and `?getValues`
for more info on this). Although this makes things easier and faster, in some cases, depending on the size of the
image and its number of layers/bands it will be unfeasible to push all the data into RAM.
However, if your raster object is too large to fit into a data frame object in memory,
you can still use R to perform K-means clustering. Packages such as __RSToolbox__ provide an implementation
of k-means that may be more suited for your case.
Check out [here](https://github.com/bleutner/RStoolbox) and
the function
`unsuperClass` [here](https://github.com/bleutner/RStoolbox/blob/9394b0297b7d7f564aca94b1bf6907f685ecd836/R/unsuperClass.R).
Also, we will need to be careful regarding `NA`'s because clustering algorithms will not run with these values
(typically throwing an error). One simple way is to use a logical index to subset the data.
Let's see how this works out in actual R code (use comments as guidance):
```{r P7_do_multi_cluster, message=FALSE, warning=FALSE, eval=FALSE, echo=TRUE}
library(cluster)
# Extract all values from the raster into a data frame
rstDF <- values(rst)
# Check NA's in the data
idx <- complete.cases(rstDF)
# Initiate the raster datasets that will hold all clustering solutions
# from 2 groups/clusters up to 12
rstKM <- raster(rst[[1]])
rstCLARA <- raster(rst[[1]])
for(nClust in 2:12){
cat("-> Clustering data for nClust =",nClust,"......")
# Perform K-means clustering
km <- kmeans(rstDF[idx,], centers = nClust, iter.max = 50)
# Perform CLARA's clustering (using manhattan distance)
cla <- clara(rstDF[idx, ], k = nClust, metric = "manhattan")
# Create a temporary integer vector for holding cluster numbers
kmClust <- vector(mode = "integer", length = ncell(rst))
claClust <- vector(mode = "integer", length = ncell(rst))
# Generate the temporary clustering vector for K-means (keeps track of NA's)
kmClust[!idx] <- NA
kmClust[idx] <- km$cluster
# Generate the temporary clustering vector for CLARA (keeps track of NA's too ;-)
claClust[!idx] <- NA
claClust[idx] <- cla$clustering
# Create a temporary raster for holding the new clustering solution
# K-means
tmpRstKM <- raster(rst[[1]])
# CLARA
tmpRstCLARA <- raster(rst[[1]])
# Set raster values with the cluster vector
# K-means
values(tmpRstKM) <- kmClust
# CLARA
values(tmpRstCLARA) <- claClust
# Stack the temporary rasters onto the final ones
if(nClust==2){
rstKM <- tmpRstKM
rstCLARA <- tmpRstCLARA
}else{
rstKM <- stack(rstKM, tmpRstKM)
rstCLARA <- stack(rstCLARA, tmpRstCLARA)
}
cat(" done!\n\n")
}
# Write the clustering solutions for each algorithm
writeRaster(rstKM,"./data-raw/LT8_PGNP_KMeans_nc2_12-1.tif", overwrite=TRUE)
writeRaster(rstCLARA,"./data-raw/LT8_PGNP_CLARA_nc2_12-1.tif", overwrite=TRUE)
```
```{r P7_load_raster_data, echo=FALSE}
rstKM <- brick("./data-raw/LT8_PGNP_KMeans_nc2_12-1.tif")
rstCLARA <- brick("./data-raw/LT8_PGNP_CLARA_nc2_12-1.tif")
```
### Evaluating unsupervised classification / clustering performance
-------------------------------------------------------------------------------------------------------
For evaluating the performance of each clustering solution and selecting the _"best"_ number of
clusters for partitioning the sample data, we will use the __silhouette Index__.
More specifically, the _silhouette_ refers to a method of interpreting and validating the consistency
within clusters of data (hence its called an _internal criteria_ in `clusterCrit` package). In a nutshell,
this method provides a graphical representation that depicts how well each clustered object lies within
its cluster. Also, the silhouette value is a measure of how similar an object is to its own cluster
(assessing intra-cluster _cohesion_) compared to other clusters (denoting between-clusters' _separation_).
The silhouette index ranges from −1 to +1, where a high value indicates that the object is well matched
to its own cluster and poorly matched to neighboring clusters. If most objects have a high value, then
the clustering configuration is considered appropriate. If many points have a low or negative value,
then the clustering configuration may have too many or too few clusters.
In R, the `clusterCrit` package provides an implementation of this internal clustering criteria in the
`intCriteria`(among many other, such as the Dunn, Ball-Hall, Davies-Bouldin, Dunn, GDI, Tau indices).
Check out `library(help="clusterCrit")` and `vignette("clusterCrit")` for more info on this package.
Now that we have defined the conceptual underpinnings of the silhouette index, we can implement
it in R code. One important detail before we proceed: since calculating the silhouette index is a
rather slow process for large numbers' of observations (>5000), we will use a stratified random
sampling approach.
This means that we will take a subset of cells from each cluster and calculate the index based on those.
We are assuming that the sample is somewhat robust and representative of the whole cells. Ideally, this
process should be repeated several times and then an average value could calculated (using a _bootstrap_
approach would also be nice here). However, for the sake of simplicity (and also because estimation
generally yields relatively low errors... you have to trust me here... `r emo::ji("wink")`) we will use
a single sample of cells in this example.
Let's see how this works out (use comments to guide you through the code):
```{r P7_calculate_clust_Perf_silhouette_idx, eval=FALSE, echo=TRUE}
library(clusterCrit)
# Start a data frame that will store all silhouette values
# for k-means and CLARA
clustPerfSI <- data.frame(nClust = 2:12, SI_KM = NA, SI_CLARA = NA)
for(i in 1:nlayers(rstKM)){ # Iterate through each layer
cat("-> Evaluating clustering performance for nClust =",(2:12)[i],"......")
# Extract random cell samples stratified by cluster
cellIdx_RstKM <- sampleStratified(rstKM[[i]], size = 2000)
cellIdx_rstCLARA <- sampleStratified(rstCLARA[[i]], size = 2000)
# Get cell values from the Stratified Random Sample from the raster
# data frame object (rstDF)
rstDFStRS_KM <- rstDF[cellIdx_RstKM[,1], ]
rstDFStRS_CLARA <- rstDF[cellIdx_rstCLARA[,1], ]
# Make sure all columns are numeric (intCriteria function is picky on this)
rstDFStRS_KM[] <- sapply(rstDFStRS_KM, as.numeric)
rstDFStRS_CLARA[] <- sapply(rstDFStRS_CLARA, as.numeric)
# Compute the sample-based Silhouette index for:
#
# K-means
clCritKM <- intCriteria(traj = rstDFStRS_KM,
part = as.integer(cellIdx_RstKM[,2]),
crit = "Silhouette")
# and CLARA
clCritCLARA <- intCriteria(traj = rstDFStRS_CLARA,
part = as.integer(cellIdx_rstCLARA[,2]),
crit = "Silhouette")
# Write the silhouette index value to clustPerfSI data frame holding
# all results
clustPerfSI[i, "SI_KM"] <- clCritKM[[1]][1]
clustPerfSI[i, "SI_CLARA"] <- clCritCLARA[[1]][1]
cat(" done!\n\n")
}
write.csv(clustPerfSI, file = "./data-raw/clustPerfSI.csv", row.names = FALSE)
```
```{r P7_load_CSV, echo=FALSE}
clustPerfSI <- read.csv("./data-raw/clustPerfSI.csv")
```
Let's print out a nice table with the silhouette index results for comparing each clustering
solution:
```{r P7_print_SI_values}
knitr::kable(clustPerfSI, digits = 3, align = "c",
col.names = c("#clusters","Avg. Silhouette (k-means)","Avg. Silhouette (CLARA)"))
```
We can also make a plot for better comparing the two algorithms:
```{r P7_silhouette_plot_clust_algos, fig.height = 4, fig.width=4.5, eval=FALSE, echo=TRUE}
plot(clustPerfSI[,1], clustPerfSI[,2],
xlim = c(1,13), ylim = range(clustPerfSI[,2:3]), type = "n",
ylab="Avg. Silhouette Index", xlab="# of clusters",
main="Silhouette index by # of clusters")
# Plot Avg Silhouette values across # of clusters for K-means
lines(clustPerfSI[,1], clustPerfSI[,2], col="red")
# Plot Avg Silhouette values across # of clusters for CLARA
lines(clustPerfSI[,1], clustPerfSI[,3], col="blue")
# Grid lines
abline(v = 1:13, lty=2, col="light grey")
abline(h = seq(0.30,0.44,0.02), lty=2, col="light grey")
legend("topright", legend=c("K-means","CLARA"), col=c("red","blue"), lty=1, lwd=1)
```
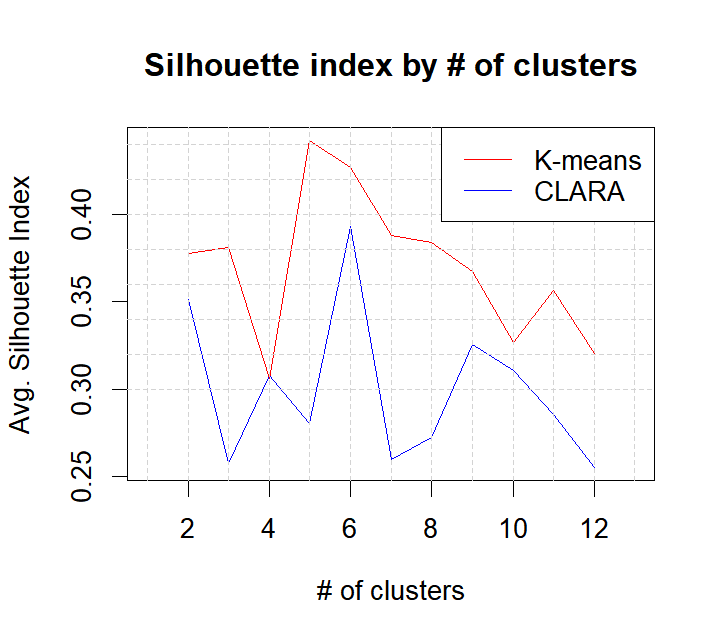
From both the table and the plot we can see widely different results in terms of clustering performance
with the __k-means algorithm performing clearly better__. This may be due to the fact that CLARA works on a
subset of the data and hence is less capable of finding the best cluster centers. In addition, for
the k-means algorithm, we can see that partioning the data into 5 groups/clusters seems to be the best option
(although 6 also seems a perfectly reasonable solution).
Finally let's make a plot of the best solution according to the silhouette index:
```{r P7_best_clust_solution, eval=FALSE, echo=TRUE}
plot(rstKM[[4]])
```
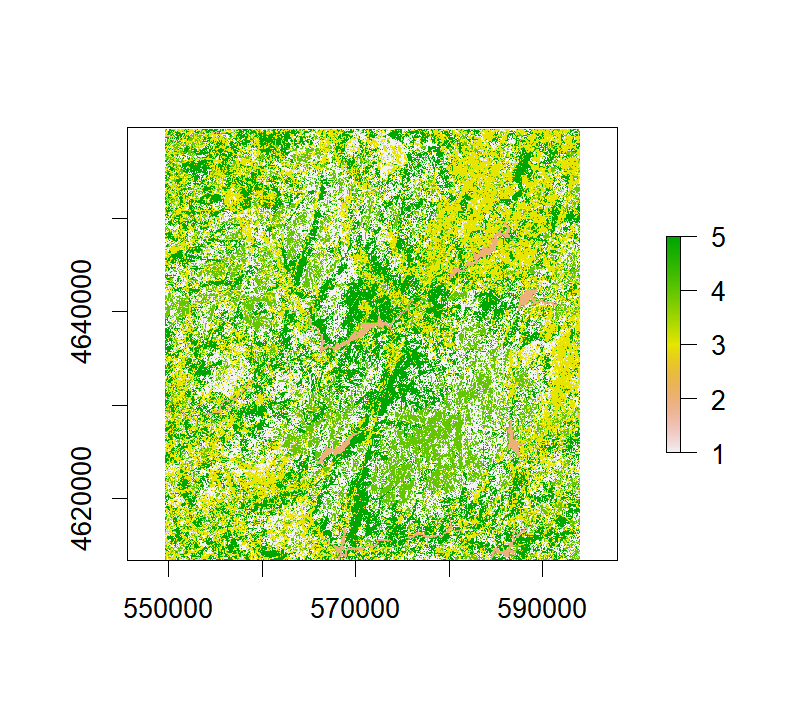
One final step (typical in the Remote Sensing domain) would be to interpret the clustering
results, analyze their spectral and land cover properties and provide a label to each cluster (e.g.,
urban, agriculture, forest). Albeit very important, that is outside the scope of this tutorial
`r emo::ji("wink")` `r emo::ji("wink")`
This concludes our exploration of the raster package and unsupervised classification for
this post. Hope you find it useful! `r emo::ji("smile")` `r emo::ji("thumbsup")` `r emo::ji("thumbsup")`