-
Notifications
You must be signed in to change notification settings - Fork 3
/
P9_rasterPackageAdvanced_III-v1.Rmd
503 lines (326 loc) · 18.4 KB
/
P9_rasterPackageAdvanced_III-v1.Rmd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
---
title: "P8 Advanced techniques with raster data (part-3) - Regression Kriging"
author: "João Gonçalves"
date: "04 December 2017"
output:
html_document:
self_contained: no
---
```{r setup, include=FALSE}
knitr::opts_chunk$set(echo = TRUE)
knitr::opts_chunk$set(fig.path = "img/")
knitr::opts_chunk$set(fig.width = 5, fig.height = 4.5, dpi = 80)
```
### Background
-------------------------------------------------------------------------------------------------------
In this post, the ninth of the geospatial processing series with raster data, I will
focus on interpolating and modelling air surface temperature data recorded at weather stations.
For this purpose I will explore __regression-kriging__ (RK), a spatial prediction technique
commonly used in geostatistics that combines a regression of the dependent variable (air
temperature in this case) on auxiliary/predictive variables (e.g., elevation, distance from shoreline)
with kriging of the regression residuals. RK is mathematically equivalent to the interpolation
method variously called universal kriging and kriging with external drift, where auxiliary
predictors are used directly to solve the kriging weights.
__Regression-kriging__ is an implementation of the best linear unbiased predictor (BLUP) for spatial
data, i.e. the best linear interpolator assuming the _universal model of spatial variation_. Hence, RK is
capable of modelling the value of a target variable at some location as a sum of a deterministic commponent
(handled by regression) and a stochastic component (kriging). In RK, both deterministic and stochastic
components of spatial variation can be modeled separately. Once the deterministic part of variation has
been estimated, the obtained residuals can be interpolated with kriging and added back to the
estimated trend.

__Regression-kriging__ is used in various fields, including meteorology, climatology, soil mapping,
geological mapping, species distribution modeling and similar. The only requirement for using RK
is that one or more covariates exist which are significantly correlated with the dependent variable.
Although powerful, RK can perform poorly if the point sample is small and non-representative of the target
variable, if the relation between the target variable and predictors is non-linear (although some non-linear
regression techniques can help on this aspect), or if the points do not represent feature space or represent
only the central part of it.
Seven regression algorithms will be used and compared through cross-validation (10-fold CV):
- Interpolation:
- Ordinary Kriging (OK)
- Regression:
- Generalized Linear Model (GLM)
- Generalized Additive Model (GAM)
- Random Forest (RF)
- Regression-kriging:
- GLM + OK of residuals
- GAM + OK of residuals
- RF + OK of residuals
The sample data used for examples is the annual average air temperature for mainland Portugal which
includes and summarizes daily records that range from 1950 to 2000. A total of 95 stations are
available, unevenly dispersed throughout the country.
Four auxiliary variables were considered as candidates to model the variation of air temperature:
- Elevation (_Elev_ in meters a.s.l.),
- Distance to the coastline (_distCoast_ in degrees);
- Latitude (_Lat_ in degrees), and,
- Longitude (_Lon_ in degrees).
One raster layer _per_ predictive variable, with a spatial resolution of 0.009 deg (ca. 1000m) in WGS 1984
Geographic Coordinate System, is available for calculating a continuous surface of temperature values.
### Model development
-------------------------------------------------------------------------------------------------------
#### Data loading and inspection
We will start by downloading and unzipping the sample data from the GitHub repository:
```{r P9_download_data_from_github, message=FALSE, warning=FALSE, paged.print=FALSE, echo=TRUE, eval=FALSE}
## Create a folder named data-raw inside the working directory to place downloaded data
if(!dir.exists("./data-raw")) dir.create("./data-raw")
## If you run into download problems try changing: method = "wget"
download.file("https://raw.githubusercontent.com/joaofgoncalves/R_exercises_raster_tutorial/master/data/CLIM_DATA_PT.zip", "./data-raw/CLIM_DATA_PT.zip", method = "auto")
## Uncompress the zip file
unzip("./data-raw/CLIM_DATA_PT.zip", exdir = "./data-raw")
```
Now, let's load the raster layers containing the predictive variables used to build
the regression model of air temperature:
```{r P9_load_data, message=FALSE, warning=FALSE}
library(raster)
# GeoTIFF file list
fl <- list.files("./data-raw/climData/rst", pattern = ".tif$", full.names = TRUE)
# Create the raster stack
rst <- stack(fl)
# Change the layer names to coincide with table data
names(rst) <- c("distCoast", "Elev", "Lat", "Lon")
```
```{r P9_raster_layers, echo=TRUE, eval=FALSE}
plot(rst)
```
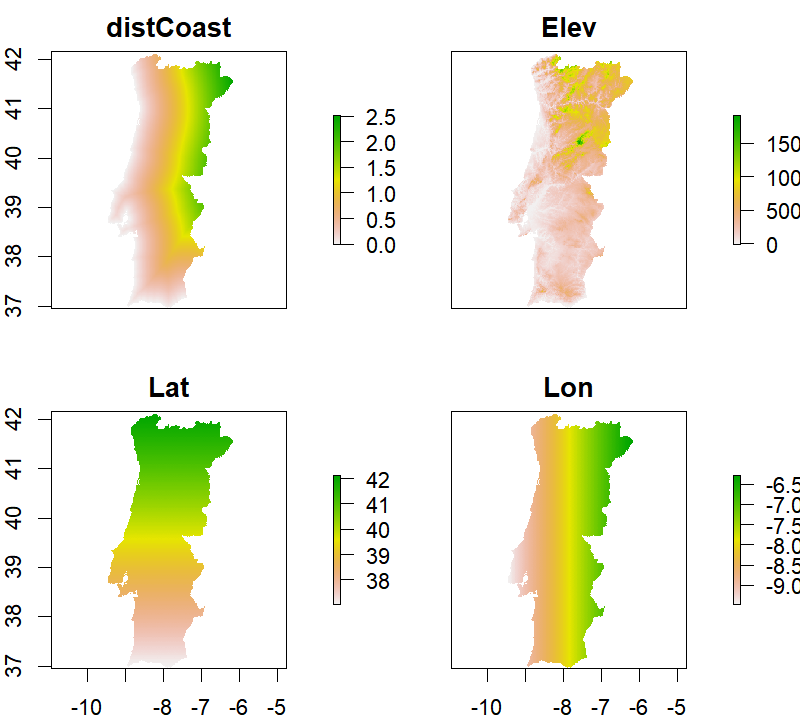
Next step, let's read the point data containing annual average temperature values along with
location and predictive variables for each weather station:
```{r P9_read_point_weather_st_data, message=FALSE, warning=FALSE}
climDataPT <- read.csv("./data-raw/ClimData/clim_data_pt.csv")
knitr::kable(head(climDataPT, n=10))
```
Based on the previous data, create a `SpatialPointsDataFrame` object to store all points and make
some preliminary plots:
```{r P9_load_as_sp, message=FALSE, warning=FALSE, paged.print=FALSE, fig.width=8}
proj4Str <- "+proj=longlat +ellps=WGS84 +datum=WGS84 +no_defs"
statPoints <- SpatialPointsDataFrame(coords = climDataPT[,c("Lon","Lat")],
data = climDataPT,
proj4string = CRS(proj4Str))
```
```{r P9_make_sp_object, eval=FALSE, echo=TRUE}
par(mfrow=c(1,2),mar=c(5,6,3,2))
plot(rst[["Elev"]], main="Elevation (meters a.s.l.) for Portugal\n and weather stations",
xlab = "Longitude", ylab="Latitude")
plot(statPoints, add=TRUE)
hist(climDataPT$AvgTemp, xlab= "Temperature (ºC)", main="Annual avg. temperature")
```

From the figure we can see that: (i) weather stations tend to cover more the areas close to
the coastline and with lower altitude, and, (ii) temperature values are 'left-skewed' with a median
equal to `r round(median(climDataPT$AvgTemp), 3)` and a median-absolute deviation (MAD) of
`r round(median(climDataPT$AvgTemp), 3)`.
Before proceeding, it is a good idea to inspect the correlation matrix to analyze the strength of
association between the response and the predictive variables. For this, we will use the package
`corrplot` with some nit graphical options `r emo::ji("thumbsup")` `r emo::ji("thumbsup")`
```{r P9_corrplot, message=FALSE, warning=FALSE, paged.print=FALSE, fig.height = 5, fig.width = 5.25, eval=FALSE, echo=TRUE}
library(corrplot)
corMat <- cor(climDataPT[,3:ncol(climDataPT)])
corrplot.mixed(corMat, number.cex=0.8, tl.cex = 0.9, tl.col = "black",
outline=FALSE, mar=c(0,0,2,2), upper="square", bg=NA)
```
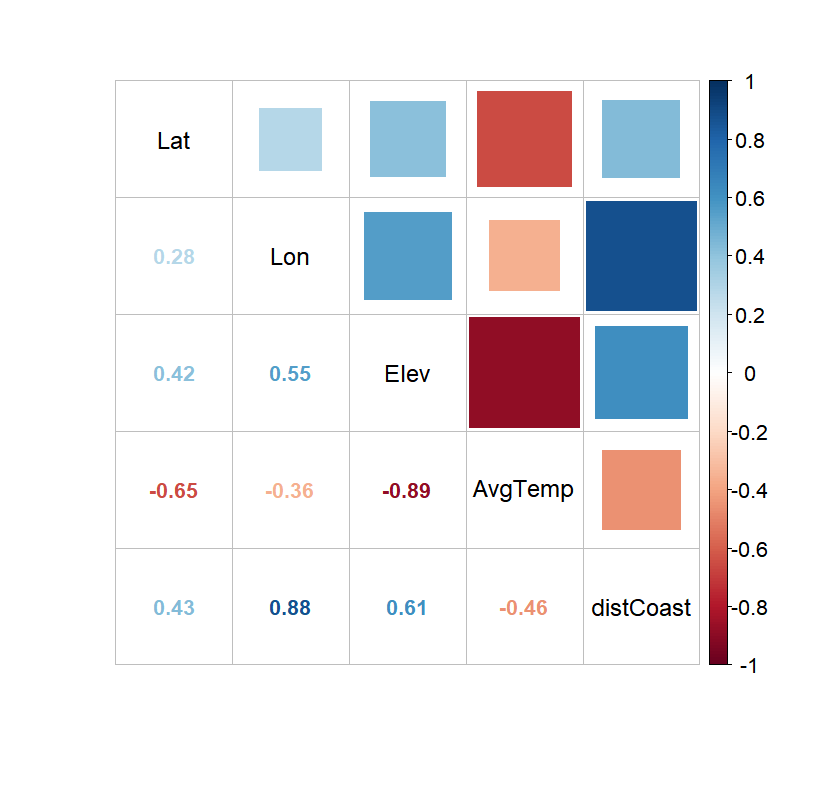
The correlation plot evidences that all predictive variables seem to be correlated with the
average temperature, especially 'Elevation' and 'Latitude' which are well-known regional controls of
temperature variation. It also shows that (as expected, given the country geometric shape) both
'Longitude' and 'Distance to the coast' are highly correlated. As such, given that 'Longitude' is
less associated to temperature and its climatic effect is less "direct" (compared to 'distCoast')
we will remove it.
#### Regression-kriging and model comparison
For comparing the different RK algorithms, we will use 10-fold cross validation and the Root-mean
square error as the evaluation metric.
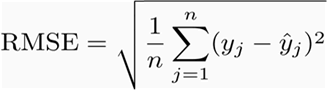
_Kriging parameters_ __nugget__, (partial) __sill__, and __range__ will be fit through Ordinary
Least Squares (OLS) from a set of previously defined values that were adjusted with the help of
some visual inspection and trial-and-error. The _Exponential_ model was selected since it gave
generally best results in preliminary analyses.

The functionalities in package `gstat` were used for all geostatistical analyses.
--------------------------------------------------------------------------------------
Now, let's define some ancillary functions for creating the k-fold train/test data splits
and for obtaining the regression residuals out of a random forest object:
```{r P9_ancillary_functions}
# Generate the K-fold train--test splits
# x are the row indices
# Outputs a list with test (or train) indices
kfoldSplit <- function(x, k=10, train=TRUE){
x <- sample(x, size = length(x), replace = FALSE)
out <- suppressWarnings(split(x, factor(1:k)))
if(train) out <- lapply(out, FUN = function(x, len) (1:len)[-x], len=length(unlist(out)))
return(out)
}
# Regression residuals from RF object
resid.RF <- function(x) return(x$y - x$predicted)
```
We also need to define some additional parameters and initialize the matrix that will store all
RMSE values (one for each training round).
```{r P9_set_some_params_init_eval_obj}
set.seed(12345)
k <- 10
kfolds <- kfoldSplit(1:nrow(climDataPT), k = 10, train = TRUE)
evalData <- matrix(NA, nrow=k, ncol=7,
dimnames = list(1:k, c("OK","RF","GLM","GAM","RF_OK","GLM_OK","GAM_OK")))
```
Now we are ready to start modelling! `r emo::ji("happy")` One code block, inside the 'for' loop, will
be used for each regression algorithm tested. Notice how (train) residuals are interpolated through
kriging and then (test) residuals are added to (test) regression results for evaluation. Use
```{r P9_model_dev_and_eval, message=FALSE, warning=FALSE}
library(randomForest)
library(mgcv)
library(gstat)
for(i in 1:k){
cat("K-fold...",i,"of",k,"....\n")
# TRAIN indices as integer
idx <- kfolds[[i]]
# TRAIN indices as a boolean vector
idxBool <- (1:nrow(climDataPT)) %in% idx
# Observed test data for the target variable
obs.test <- climDataPT[!idxBool, "AvgTemp"]
## ----------------------------------------------------------------------------- ##
## Ordinary Kriging ----
## ----------------------------------------------------------------------------- ##
# Make variogram
formMod <- AvgTemp ~ 1
mod <- vgm(model = "Exp", psill = 3, range = 100, nugget = 0.5)
variog <- variogram(formMod, statPoints[idxBool, ])
# Variogram fitting by Ordinary Least Sqaure
variogFitOLS<-fit.variogram(variog, model = mod, fit.method = 6)
#plot(variog, variogFitOLS, main="OLS Model")
# kriging predictions
OK <- krige(formula = formMod ,
locations = statPoints[idxBool, ],
model = variogFitOLS,
newdata = statPoints[!idxBool, ],
debug.level = 0)
ok.pred.test <- OK@data$var1.pred
evalData[i,"OK"] <- sqrt(mean((ok.pred.test - obs.test)^2))
## ----------------------------------------------------------------------------- ##
## RF calibration ----
## ----------------------------------------------------------------------------- ##
RF <- randomForest(y = climDataPT[idx, "AvgTemp"],
x = climDataPT[idx, c("Lat","Elev","distCoast")],
ntree = 500,
mtry = 2)
rf.pred.test <- predict(RF, newdata = climDataPT[-idx,], type="response")
evalData[i,"RF"] <- sqrt(mean((rf.pred.test - obs.test)^2))
# Ordinary Kriging of Random Forest residuals
#
statPointsTMP <- statPoints[idxBool, ]
statPointsTMP@data <- cbind(statPointsTMP@data, residRF = resid.RF(RF))
formMod <- residRF ~ 1
mod <- vgm(model = "Exp", psill = 0.6, range = 10, nugget = 0.01)
variog <- variogram(formMod, statPointsTMP)
# Variogram fitting by Ordinary Least Sqaure
variogFitOLS<-fit.variogram(variog, model = mod, fit.method = 6)
#plot(variog, variogFitOLS, main="OLS Model")
# kriging predictions
RF.OK <- krige(formula = formMod ,
locations = statPointsTMP,
model = variogFitOLS,
newdata = statPoints[!idxBool, ],
debug.level = 0)
rf.ok.pred.test <- rf.pred.test + RF.OK@data$var1.pred
evalData[i,"RF_OK"] <- sqrt(mean((rf.ok.pred.test - obs.test)^2))
## ----------------------------------------------------------------------------- ##
## GLM calibration ----
## ----------------------------------------------------------------------------- ##
GLM <- glm(formula = AvgTemp ~ Elev + Lat + distCoast, data = climDataPT[idx, ])
glm.pred.test <- predict(GLM, newdata = climDataPT[-idx,], type="response")
evalData[i,"GLM"] <- sqrt(mean((glm.pred.test - obs.test)^2))
# Ordinary Kriging of GLM residuals
#
statPointsTMP <- statPoints[idxBool, ]
statPointsTMP@data <- cbind(statPointsTMP@data, residGLM = resid(GLM))
formMod <- residGLM ~ 1
mod <- vgm(model = "Exp", psill = 0.4, range = 10, nugget = 0.01)
variog <- variogram(formMod, statPointsTMP)
# Variogram fitting by Ordinary Least Sqaure
variogFitOLS<-fit.variogram(variog, model = mod, fit.method = 6)
#plot(variog, variogFitOLS, main="OLS Model")
# kriging predictions
GLM.OK <- krige(formula = formMod ,
locations = statPointsTMP,
model = variogFitOLS,
newdata = statPoints[!idxBool, ],
debug.level = 0)
glm.ok.pred.test <- glm.pred.test + GLM.OK@data$var1.pred
evalData[i,"GLM_OK"] <- sqrt(mean((glm.ok.pred.test - obs.test)^2))
## ----------------------------------------------------------------------------- ##
## GAM calibration ----
## ----------------------------------------------------------------------------- ##
GAM <- gam(formula = AvgTemp ~ s(Elev) + s(Lat) + s(distCoast), data = climDataPT[idx, ])
gam.pred.test <- predict(GAM, newdata = climDataPT[-idx,], type="response")
evalData[i,"GAM"] <- sqrt(mean((gam.pred.test - obs.test)^2))
# Ordinary Kriging of GAM residuals
#
statPointsTMP <- statPoints[idxBool, ]
statPointsTMP@data <- cbind(statPointsTMP@data, residGAM = resid(GAM))
formMod <- residGAM ~ 1
mod <- vgm(model = "Exp", psill = 0.3, range = 10, nugget = 0.01)
variog <- variogram(formMod, statPointsTMP)
# Variogram fitting by Ordinary Least Sqaure
variogFitOLS<-fit.variogram(variog, model = mod, fit.method = 6)
#plot(variog, variogFitOLS, main="OLS Model")
# kriging predictions
GAM.OK <- krige(formula = formMod ,
locations = statPointsTMP,
model = variogFitOLS,
newdata = statPoints[!idxBool, ],
debug.level = 0)
gam.ok.pred.test <- gam.pred.test + GAM.OK@data$var1.pred
evalData[i,"GAM_OK"] <- sqrt(mean((gam.ok.pred.test - obs.test)^2))
}
```
Let's check the average and st.-dev. results for the 10-folds CV:
```{r P9_average_RMSE_results}
round(apply(evalData,2,FUN = function(x,...) c(mean(x,...),sd(x,...))),3)
```
From the results above we can see that RK performed generally better than
the regression techniques alone or tahn Ordinary Kriging. The __GAM-based RK method
obtained the best scores__ with a RMSE of ca. `r round(mean(evalData[,"GAM_OK"]), 3)`.
These are pretty good results!! `r emo::ji("happy")` `r emo::ji("thumbsup")` `r emo::ji("thumbsup")`
To finalize, we will predict the temperature values for the entire surface of mainland Portugal
based on GAM-based Regression Kriging, which was the best performing technique on the test. For this
we will not use any test/train partition but the entire dataset:
```{r P9_GAM_modelling}
GAM <- gam(formula = AvgTemp ~ s(Elev) + s(Lat) + s(distCoast), data = climDataPT)
rstPredGAM <- predict(rst, GAM, type="response")
```
Next we need to obtain a surface with kriging-interpolated residuals. For that, we have to
convert the input `RasterStack` or `RasterLayer` into a `SpatialPixelsDataFrame` so that
the `krige` function can use it as a reference:
```{r P9_create_spatial_pixels_DF}
rstPixDF <- as(rst[[1]], "SpatialPixelsDataFrame")
```
Like before, we will interpolate the regression residuals with kriging and add them
back to the regression results.
```{r P9_krig_resid, message=FALSE, warning=FALSE, paged.print=FALSE, eval=FALSE, echo=TRUE}
# Create a temporary SpatialPointsDF object to store GAM residuals
statPointsTMP <- statPoints
crs(statPointsTMP) <- crs(rstPixDF)
statPointsTMP@data <- cbind(statPointsTMP@data, residGAM = resid(GAM))
# Define the kriging parameters and fit the variogram using OLS
formMod <- residGAM ~ 1
mod <- vgm(model = "Exp", psill = 0.15, range = 10, nugget = 0.01)
variog <- variogram(formMod, statPointsTMP)
variogFitOLS <- fit.variogram(variog, model = mod, fit.method = 6)
# Plot the results
plot(variog, variogFitOLS, main="Semi-variogram of GAM residuals")
```

The exponential semi-variogram looks reasonable although some lack-of-convergence problems...
`r emo::ji("worried")` `r emo::ji("pensive")`
Finally, let's check the average temperature map obtained from GAM RK:
```{r P9_final_map, fig.height=8, fig.width=5, eval=FALSE, echo=TRUE}
residKrigMap <- krige(formula = formMod ,
locations = statPointsTMP,
model = variogFitOLS,
newdata = rstPixDF)
residKrigRstLayer <- as(residKrigMap, "RasterLayer")
gamKrigMap <- rstPredGAM + residKrigRstLayer
plot(gamKrigMap, main="Annual average air temperature\n(GAM regression-kriging)",
xlab="Longitude", ylab="Latitude", cex.main=0.8, cex.axis=0.7, cex=0.8)
```

This concludes our exploration of the raster package and regression kriging for
this post. Hope you find it useful! `r emo::ji("smile")` `r emo::ji("thumbsup")` `r emo::ji("thumbsup")`