Point-free style is a paradigm in which function definitions do not include information about its arguments. Instead, functions are defined in terms of combinators and composition (Wikipedia). Hee is a concatenative, functional programming language built for no practical purpose -- my goal is to use it as a vehicle for understanding PL topics.
Hee is in the very early stages of development. Some aspects of the syntax haven't settled enough to allow providing examples. This includes the type syntax, comments, function declarations, and type declarations. The general goal is to keep the concrete syntax as minimal as possible, so I'm still looking for ways to implement these features without adding "extra" syntax.
The preliminary type system is not usable. Several issues must be addressed before certain simple terms can be correctly typed. Some terms that pose interesting problems are:
-
dup compose, becauseA (B → B) → A (B → B)is not sufficiently general. This is the type inferred by HM for the analogous lambda calculus expressionλf x. f (f x). We should be able to derive a principle type for it that admits expressions like[+] dup composeand[33] dup compose. -
dupitself which seems to break concatenativity without impredicative polymorphism. That is,[id] [id]has the type(∀T. T → T) (∀U. U → U), so we should assign[id] dupthe same type. Without impredicative polymorphism we will derive∀T. (T → T) (T → T)instead. -
dup unquote, the U-combinator, requires recursive types. This permits general recursion.
I'm starting from a clean slate in Haskell. Prerequisites include ghc 7.4 and haskell-platform 2012.
$ git clone git://github.com/kputnam/hee.git
$ cd hee
$ cabal install
$ cat examples/test.hee
increment
: num -> num
" doc string follows type (and is optional)
= 1 +
decrement
" types declarations are optional
= 1 -
main
= 10
increment
decrement
10 ==
$ cat examples/test.hee | hee-parse
[DNameBind "inc"
(Just "num -> num")
(Just " doc string follows type (and is optional)\n")
(ECompose (ELiteral (LInteger Decimal 1)) (EName "+"))
,DNameBind "decrement"
(Just " type declarations are optional\n")
(ECompose (ELiteral (LInteger Decimal 1)) (EName "-"))
,DNameBind "main"
Nothing
Nothing
(ECompose
(ELiteral (LInteger Decimal 10))
(ECompose
(EName "increment")
(ECompose
(EName "decrement")
(ECompose
(ELiteral (LInteger Decimal 10))
(EName "==")))))]
Programs must be a set of top-level declarations (no top-level expressions
will be parsed). The main definition will be executed.
$ echo 'main = 5 [swap dup 1 <= [pop pop 1] [dup 1 - dig u *] if] u' | hee-eval
120
Note that type declarations are currently ignored and there are no static type checks.
$ cabal configure --enable-tests
$ cabal build
$ cabal test
There is a type checker that serves as a proof of concept in
attic/src/main/haskell. You can
infer the type of expressions like so:
attic$ rake hee:check 'swap cons swap cons swap cons'
"swap cons swap cons swap cons"
"(A a a a ([] a) -> A ([] a))"
The above type states, given a stack with three elements (of the same type a)
and a list of elements, the expression will produce a list of a elements.
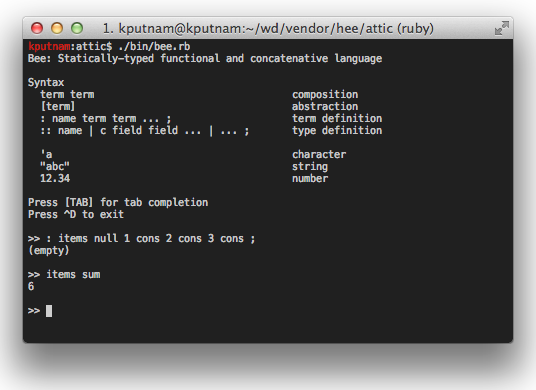
There's a REPL written in Ruby, in attic/bin/bee.rb.
This includes a few features like tab-completion, execution traces, and the
ability to save definitions created in the REPL to an external file. The
interpreter achieves tail-call optimization easily because it effectively
implements subroutine threading.
There is a small runtime library in attic/runtime
directory that is loaded when the REPL starts. Mostly this includes some type
definitions, like lists and booleans with a number of functions to operate on
these types. These files include what appears to be module declarations and
comments, however these are parsed as top-level expressions which are discarded
by the parser. The parser only reads definitions from files.
My primary motivations for developing hee are to gain a deeper theoretical and practical understanding of programming languages and type systems. I am less concerned with developing a practically usable language.
For example, one motivation behind using postfix syntax is it is simple to parse, though may be harder for humans to read and write. Using point-free notation means the symbol table doesn't need to maintain information about the current scope: there are no "local variables". These kinds of choices simplify the language implementation, and may (or may not) yield benefits for programmers using the language.
Some features I'd like to explore include:
- Module systems
- Type inference
- Quasiquotation
- Interactive development
- Comprehensible type errors
Like many stack-based languages, hee uses an postfix syntax for expression.
Operands are written before operators, e.g. 1 3 +.
κ,ι ::= @ -- stack
| * -- manifest
| κ → ι -- function
Kinds classify types. Hee distinguishes stack-types, value-types, and type constructors from one another.
Stacks (rows), with kind @
σ,φ ::= ∅ -- empty
| S,T -- type variable
| σ τ -- non-empty stack
Values, with kind *
τ,υ ::= a,b -- type variable
| σ → φ -- function on stacks
| int
| str
| ...
Currently the type system is too under-powered to be useful. Several features like quantified types, qualified types, type constructors, type classes, and higher-rank polymorphism are intended, once I understand them better.
e,f ::= ∅ -- empty (identity)
| e f -- composition
| [e] -- abstraction
| name -- top-level definition
| literal -- char, num, str, etc
Unlike an applicative language, terms are built entirely by function composition.
For instance, + * composes an addition with a multiplication. Similarly, 1 +
composes a function 1 that pushes the numeric value one on the stack with a
function + that pops the top two stack elements and pushes their sum.
These combinators are used to manipulate abstractions (function values). Here are some of the type signatures:
quote
: S a → S (T → T a)
" convert a value to an abstraction that yields that value
compose
: S (T → U) (U → V) → S (T → V)
" composes two abstractions, eg [3] [4] compose ==> [3 4]
unquote
: S (S → T) → T
" applies an abstraction, eg [3] unquote ==> 3
dip
: S a (S → T) → T a
" applies an abstraction, eg 4 [3] dip ==> 3 4
Because arguments aren't explicitly named, they must be accessed according to their position on the stack. Several stack-shuffling combinators are provided to move values around. Below are type signatures of some of these:
pop : S a → S
dup : S a → S a a
swap : S a b → S b a
over : S a b → S a b a
dig : S a b c → S b c a
Declaring an algebraic data type implicitly creates a deconstructor. This is a
function which takes function arguments corresponding to each constructor, in
the same order as the constructor definitions. For instance, true ["T"] ["F"] unboolean yields "T". Note if is nothing more than unboolean.
:: boolean
| true
| false
;
-- unboolean is created implicitly
-- unboolean : S boolean (S → T) (S → T) → T
Boolean operators can be implemented like so:
: not [false] [true] unboolean ;
: and [id] [pop false] unboolean ;
: or [pop true] [id] unboolean ;
Like other languages with algebraic data types, each constructor can wrap any fixed number of values. The current notation is inadequate for type checking, and the field names are ignored -- this will change.
:: list
| null
| cons tail head
;
-- unlist is created implicitly
-- unlist : S a-list (S → T) (S a-list a → T) → T
In most non stack-based languages, functions can return at most one value. Multiple values can be simulated by packing them into a single value, and then unpacking them in the caller.
nextFree :: Int → [Int] → (Int, [Int])
nextFree current [] = (current+1, [])
nextFree current (v:vs) = if current+1 < v
then (current+1, v:vs)
else nextFree v vs
In a stack-based language, "functions" can return any number of values,
including zero, by pushing them onto the stack. For example, the next-free
function, given a sorted list of bound ids and a starting point, shrinks
the list of bound ids that need to searched on the next call, and also
returns the next free id.
: next-free -- S num-list num → S num-list num
swap -- id xs
[1 + null swap] -- id → null id'
[dig 1 + 2dup > -- id xs' x → xs' x id' → xs' x id' bool
[[cons] dip] -- xs' x id' → xs id'
[pop next-free] -- xs' x id' → ...
if]
unlist ;
This lets us call next-free like so:
-- define a list of integers: 2, 4, 5
: bound-vars null 5 cons 4 cons 2 cons ;
bound-vars -1 -- (2,4,5) -1
next-free -- (2,4,5) 0
next-free -- (2,4,5) 1
next-free -- (4,5) 3
next-free -- () 6
next-free -- () 7
Hee doesn't have lexical scopes, mutable bindings, or parameter names so closures as we know them aren't meaningful. However, we can exploit other features of the language to achieve similar results.
: generate-free' -- xs x
next-free -- xs' x'
swap quote -- x' [xs']
over quote -- x' [xs'] [x']
[generate-free'] -- x' [xs'] [x'] [generate-free']
compose compose ; -- x' [xs' x' generate-free']
Values can be lifted to functions using quote, and functions can be composed
with compose. This enables immutable state to be encapsulated inside a function.
: generate-free
quote [-1 generate-free'] compose ;
These two features also enable partial application, e.g. [-1 generate-free'].
Using this technique we have hidden the list of unbound ids from the caller.
bound-vars -- [2,4,5]
generate-free -- [...]
unquote -- 0 [...]
unquote -- 0 1 [...]
unquote -- 0 1 3 [...]
unquote -- 0 1 3 6 [...]
Each time the function is applied, it produces the next free variable and also produces the next function which embeds any necessary state to generate the remaining free ids.
Each rule corresponds to one of the syntactical forms for terms
T-EMPTY -----------
∅ : S → S
e : S → T f : T → U
T-COMPOSE ------------------------
e f : S → U
e : S → T
T-QUOTE ---------------------
[e] : U → U (S → T)
Γ(name) = S → T
T-NAME ------------------
name : S → T
T-LITERAL ------------------------------------------------------------
1 : S → S int 'a : S → S char "x" : S → S str ...
The type context Γ is elided from most rules for brevity, and also because expressions cannot extend it during computation. That is, only top-level definitions (not expressions) can bind values to names.
Consider the expression swap compose unquote 1 +. We'll perform type inference
on this expression by evaluating one type judgement at a time.
First, swap. This is viewed as a composition with the empty term, so we'll
use T-COMPOSE to infer the type of ∅ swap.
e : S → T f : T → U
- - .---. .---.
∅ : S → S swap : A b c → A c b
---------------------------------- T-COMPOSE
∅ swap : A b c → A c b
'----' '---'
e f : S → U
So the pre-conditions of T-COMPOSE are unified with the types of ∅ and
swap. That is, S = S, T = S, T = A b c, and U = A c b. We perform
unification on the two equations for T, which yields the substitution:
S = A b c
We apply this substitution to the post-condition of T-COMPOSE, which is
S → U. This yields the type of ∅ swap : A b c → A c b. This shows that
composition with the empty term ∅ is unsurprisingly trivial.
Now we compose swap with the term compose, which follows similar steps.
S → T T → U
.---. .---. .---------------. .-------.
swap : A b c → A c b compose : D (E → F) (F → G) → D (E → G)
----------------------------------------------------------------- T-COMPOSE
swap compose : A (F → G) (E → F) → A (E → G)
We've unified both equations for T from the premise of the T-COMPOSE
rule: A c b with D (E → F) (F → G), resulting in the substitution:
c = E → F
b = F → G
Then we can apply that substitution to S → T, the conclusion of T-COMPOSE,
which gives us swap compose : A (F → G) (E → F) → A (E → G).
Next, compose the term swap compose with the term unquote:
S → T T → U
.---------------. .-------. .-------. -
swap compose : A (F → G) (E → F) → A (E → G) unquote : H (H → I) → I
----------------------------------------------------------------------- T-COMPOSE
swap compose unquote : A (F → G) (A → F) → G
Here we unify A (E → G) with H (H → I), resulting in the substitution
I = G
H = E
H = A
E = A
This time, the constraints propagated backward to the input S. Now the
function at the top of the stack must have the domain A, matching the stack
below the second element. Previously, its domain was E which was unrelated
to A.
Lastly, we compose the term swap compose unquote with the term +:
S → T T → U
.---------------. - .-------. .---.
swap compose unquote : A (F → G) (A → F) → G + : K int int → K int
--------------------------------------------------------------------- T-COMPOSE
swap compose unquote + : A (F → K int int) (A → F) → K int
Like before, we unify G with K int int, resulting in the substitution:
G = K int int
Then we apply this substitution to S → U, which is A (F → G) (A → F) → K int
in this case. Notice again that constraints propagated so we've restricted the
type of the input merely by composing with another term.