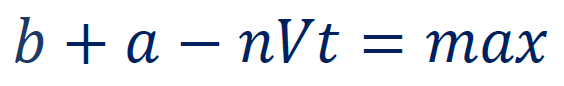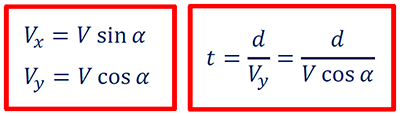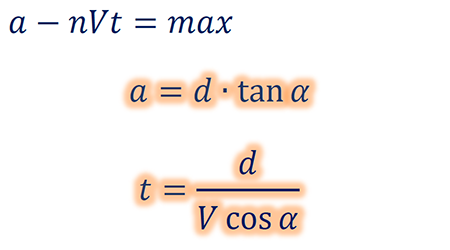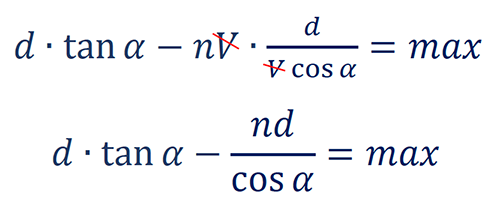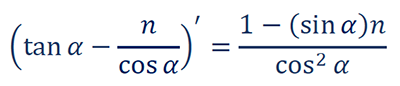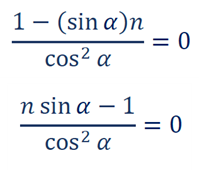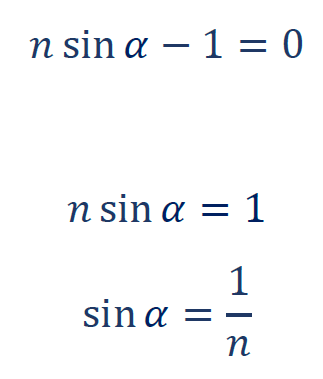In Georgian (ქართული): https://drive.google.com/file/d/0B_4P3RNorJzTN3h0Z3cwaG04SXc
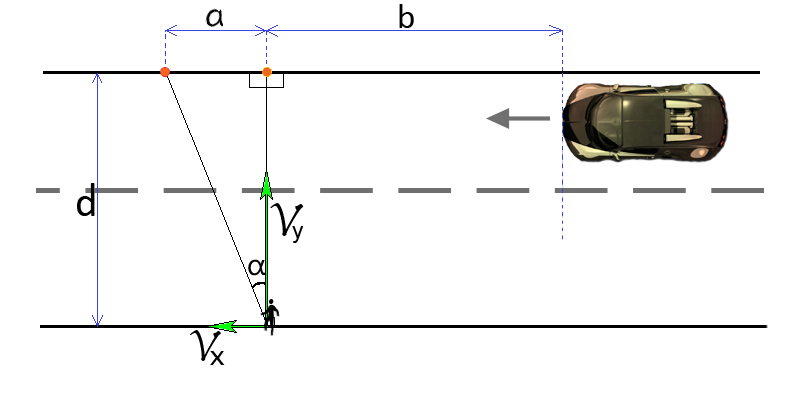
The car has n times more speed than the pedestrian. What is the best α angle from the perpendicular to maximize the chance of crossing the road in time before the car approaches?
1) n > 1
2) 0 ≤ α < 90°
3) The width of the road is unknown
4) The distance between the car and the pedestrian is unknown
In order to get the best angle with maximum probability of crossing the road before the car approaches ---- when the pedestrian crosses the road, the distance between the car and him/her must be maximum:
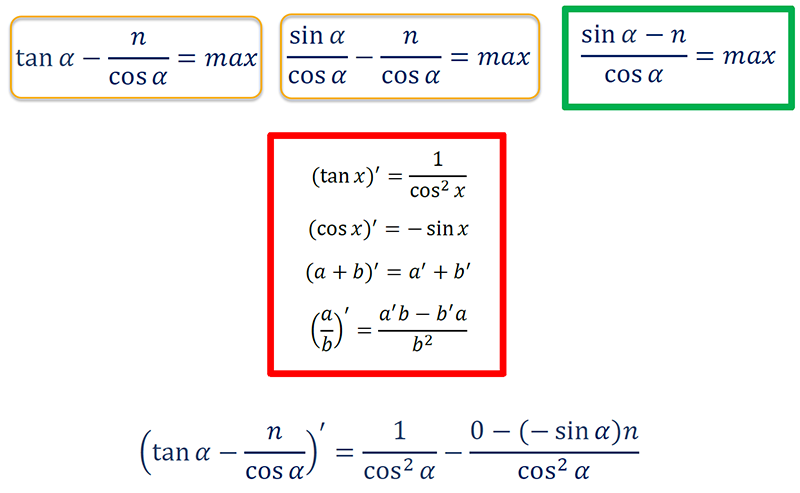
First, define the variables:
Speed of the pedestrian — V
Speed of the car — n⋅V
Horizontal speed of the pedestrian — Vx
Vertical speed of the pedestrian — Vy
Horizontal distance between the first and the last point of the pedestrian — a (not α)
Horizontal distance between the car and the pedestrian — b
Width of the road — d
Time spent to cross the road — t
b affects the maximum, but it does not affect the best angle to get maximum, so we can remove it.
d affects the maximum, but it does not affect the best angle to get maximum, so we can remove it.
In order to find the extremum of a function, we must equalize its derivative to zero:
cos2(α) cannot be zero, so α cannot be 90°, and therefore:
And finally, α = arcsin(1/n) because we already knew that 0 ≤ α < 90° and n > 1.
α = arcsin(1/n)
| n (n > 1) | α (0 ≤ α < 90°) |
|---|---|
| 1.1 | ≈65.380023° |
| 1.5 | ≈41.810315° |
| 2 | =30° |
| 3 | ≈19.471221° |
| 4 | ≈14.477512° |
| 5 | ≈11.536959° |
| 10 | ≈5.73917° |
| 15 | ≈3.822554° |
| 20 | ≈2.865984° |
| 50 | ≈1.145992° |
| 100 | ≈0.572967° |
| 1000 | ≈0.057296° |
y = b + d ⋅ tan(α) - n⋅V⋅d/(V ⋅ cos(α))
and
α = arcsin(1/n)
https://www.geogebra.org/m/YV7g2YKA