显式几何表示方式: 三角形顶点, 贝塞尔曲面, 细分曲面, 非均匀有理B样条(NURBS), 点云,
如何用三角形面来表示物体呢?
和编译出来的 obj 不一样, 这里的 obj 是文本文件

这里描述的是一个立方体, 所以有 8 2111个顶点v. 另外还描述了 6 个法线vn (因为有公用所以重复了2个). 另外如何用三角形描述面呢? 关注 f 开头的描述 f 第n个点/纹理坐标/法线 ...
https://zhuanlan.zhihu.com/p/38052123
https://www.jianshu.com/p/f7f3e7b6ebf5
v 1.00 -1.00 -1.00 表示一个点
vt 0.74 0.75 vt 表示纹理坐标
vn -1.00 0.00 0.00 法线坐标
f 1/1/1 2/2/1 3/3/1 三个点组成的面
f v1/vt1 v2/vt2 v3/vt3 ... 顶点纹理索引 1个斜杠/
f v1/vt1/vn1 v2/vt2/vn2 v3/vt3/vn3 顶点纹理法线索引 2个/
f v1//vn1 v2//vn2 v3//vn3 顶点法线索引 也是2个/ 中间的值不写
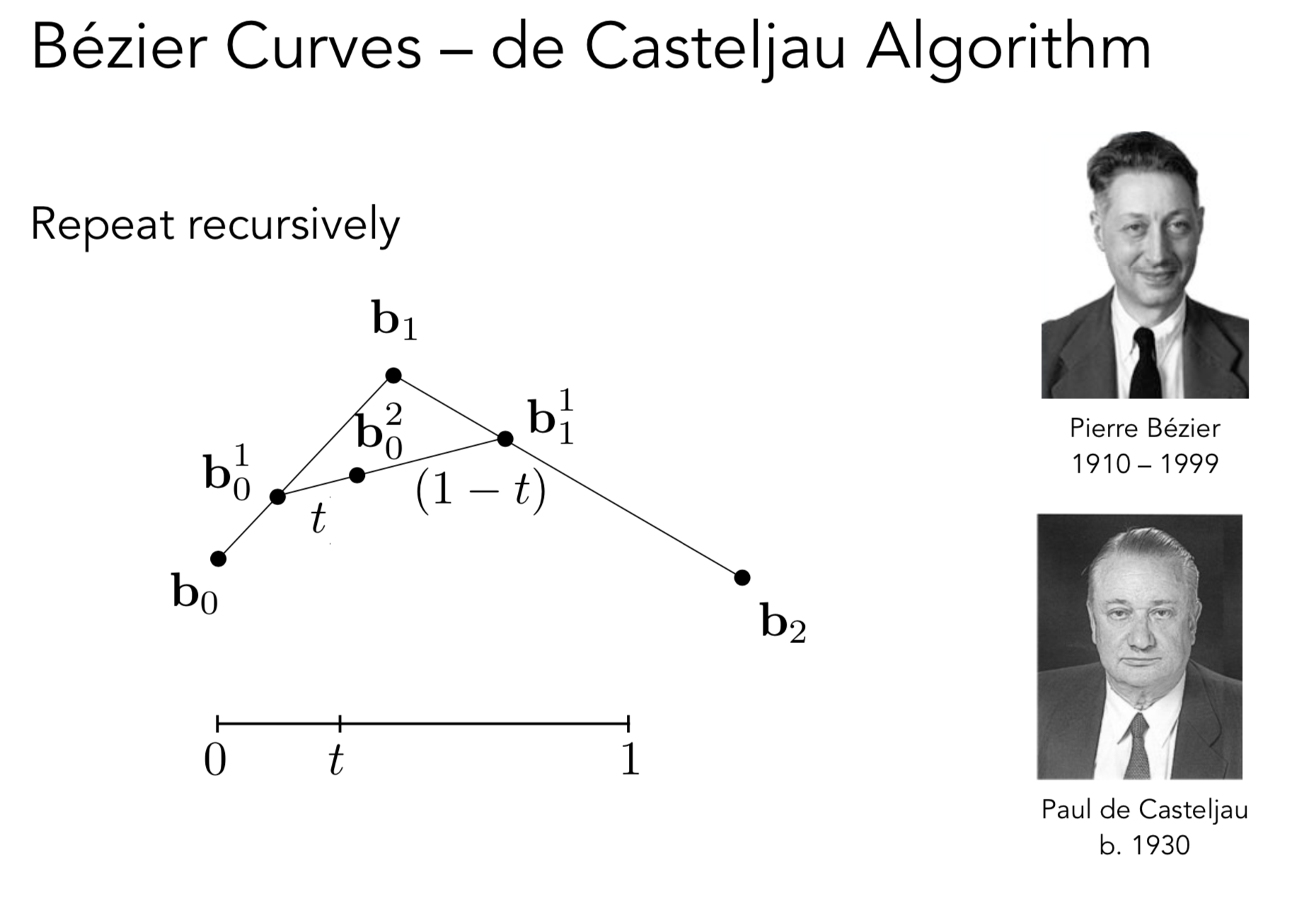
用一系列控制点去定义曲线
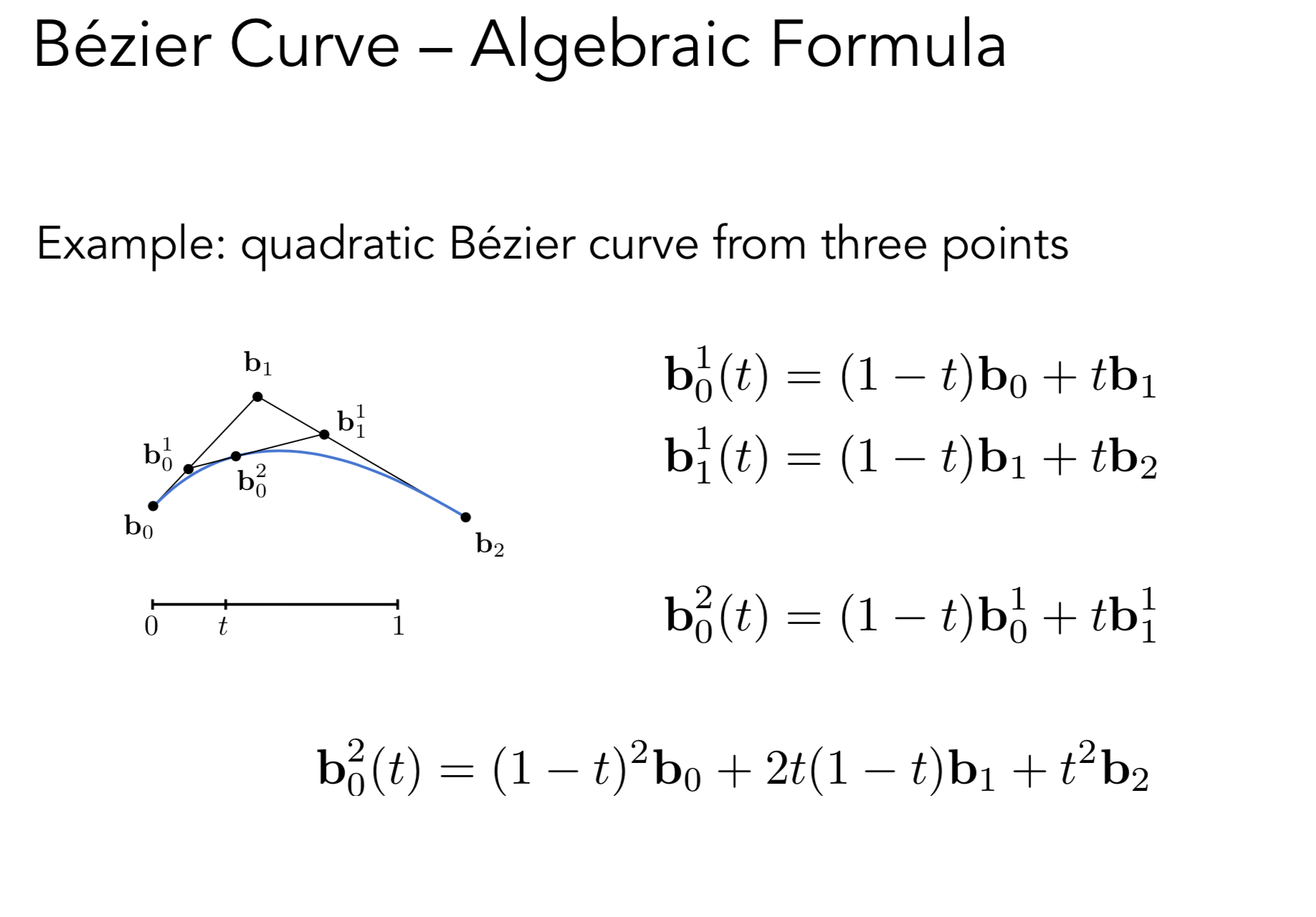
给定三个点: 生成二次贝塞尔曲线
t 代表时间
b02 这个点表示时间t的时候 曲线所在的位置
PS 曲线并不一定要经过控制点 只要经过起始点和结束点就行
绘制贝塞尔曲线的方法
https://blog.csdn.net/lafengxiaoyu/article/details/56294678
https://blog.csdn.net/venshine/article/details/51758841
https://github.com/venshine/BezierMaker
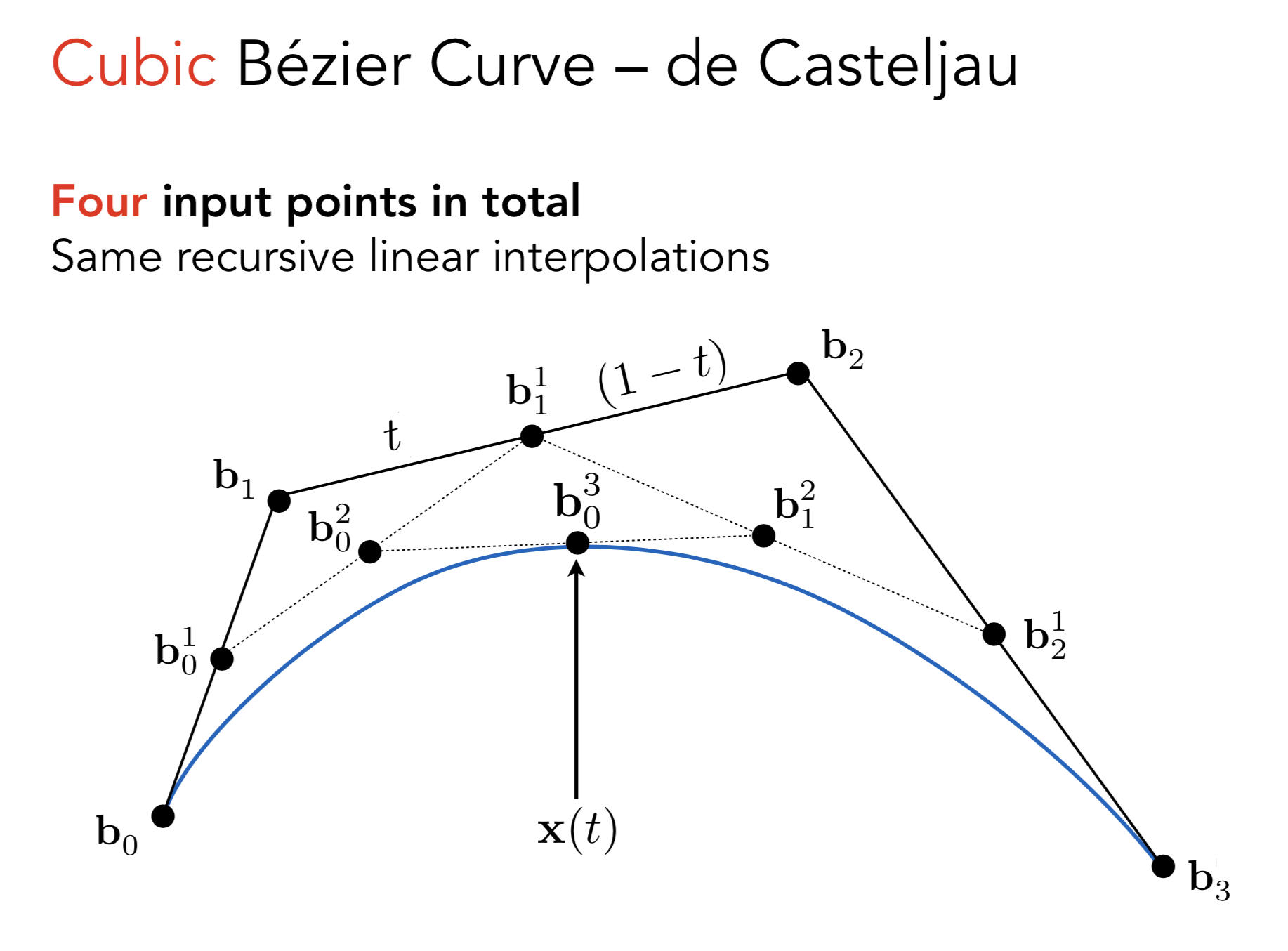
对于4个控制点的情形:
从原来4个点 3条线段(b0b1 b1b2 b2b3)
变为三个点两条线段(b01b11 b11 b21) 问题规模缩小了
递归扫什么程度呢? 到三点在一条线上的时候 (就上一个图那样)
四个控制点的贝塞尔曲线, 也就是三次贝塞尔曲线 Cubic Bezier
t = 0的时候 就应该是b0
t = 1 的时候 就是 b1
b01t 是 b0和b1做线性插值得到
b0 应该时间t 距离b0 的距离 也就是 1-t
b02 是 b01 b11 做线性插值得到
该公式描述了 n+1 个(从0~1)控制点
下面的公式是一个二项分布的多项式 竖着的(n, i)表示 n 里面选择 i
1 3 3 1 二项式定理(杨辉三角)
 贝塞尔曲线当然不仅仅是局限在平面上, 3维空间中的点一样适用
贝塞尔曲线当然不仅仅是局限在平面上, 3维空间中的点一样适用
性质2 对于4个控制点的三次贝塞尔曲线来说, b'(0)的切线是 3(b1 - b0)???
性质3 贝塞尔曲线在仿射变换下的性质 (放射不变性) :
对控制点做了仿射变换之后, 这些控制点形成的贝塞尔曲线 == 根据这些控制点做出贝塞尔曲线做仿射变换之后得到的曲线.
但是其他变换不行, 比如投影变换
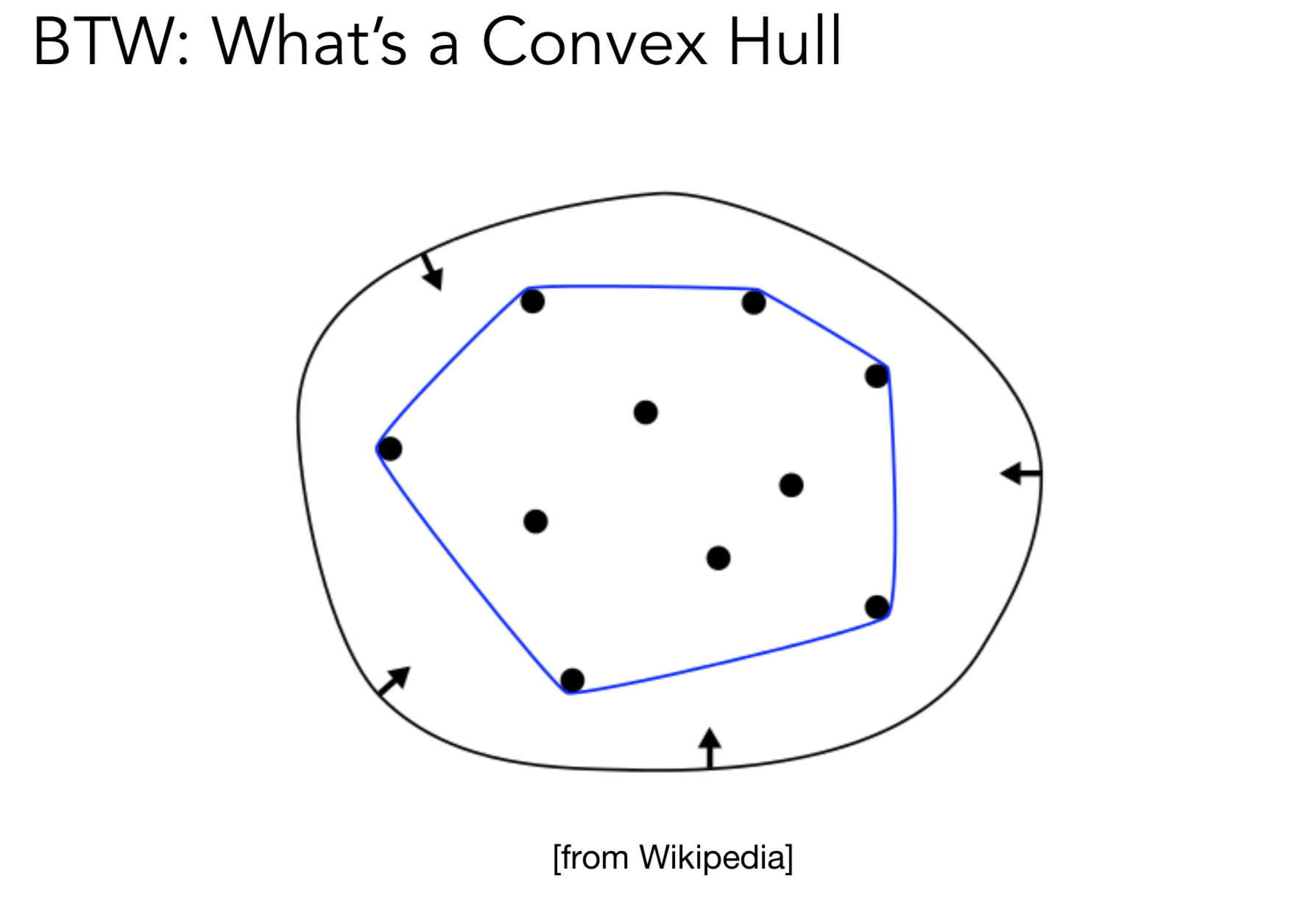
性质4 画出的贝塞尔曲线一定在控制点形成的凸包内
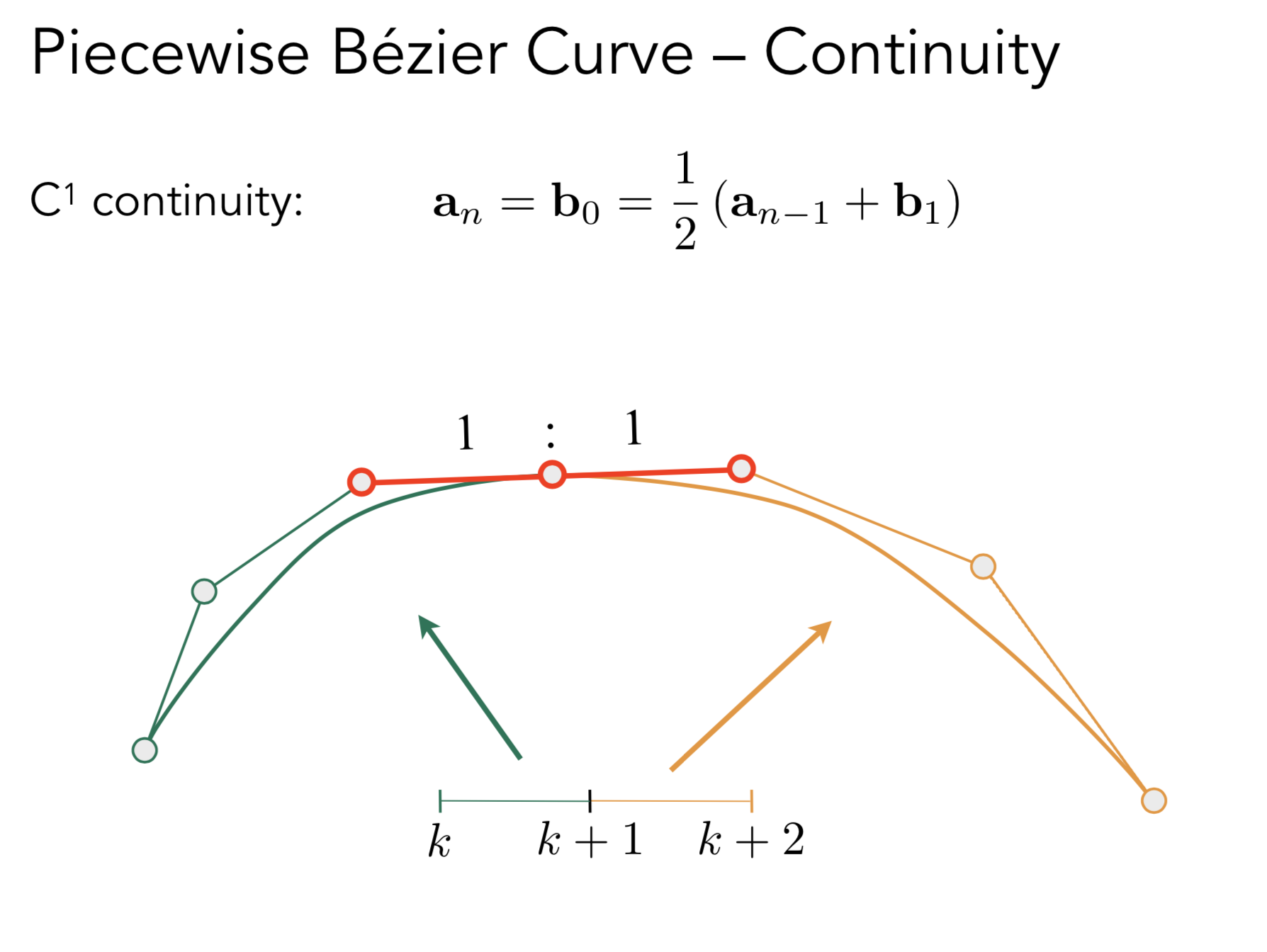
一般人们习惯使用4个控制点去定义一条曲线, 下面这个曲线由多段贝塞尔曲线构成
为了保证多个贝塞尔曲线的光滑性质 新增的线段的控制点要和原先最后两个的控制点形成的线段共线 , 且长度相等.
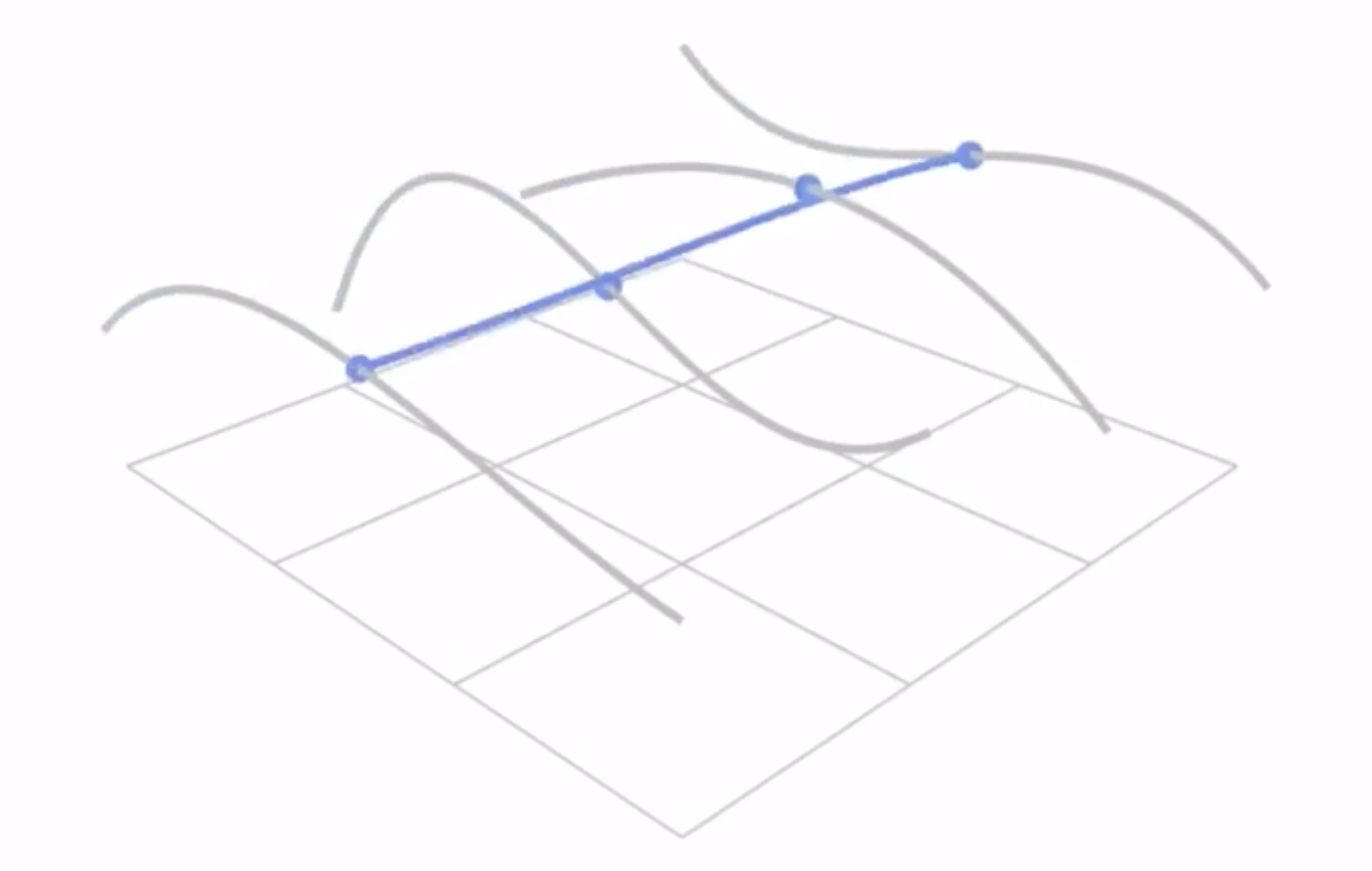
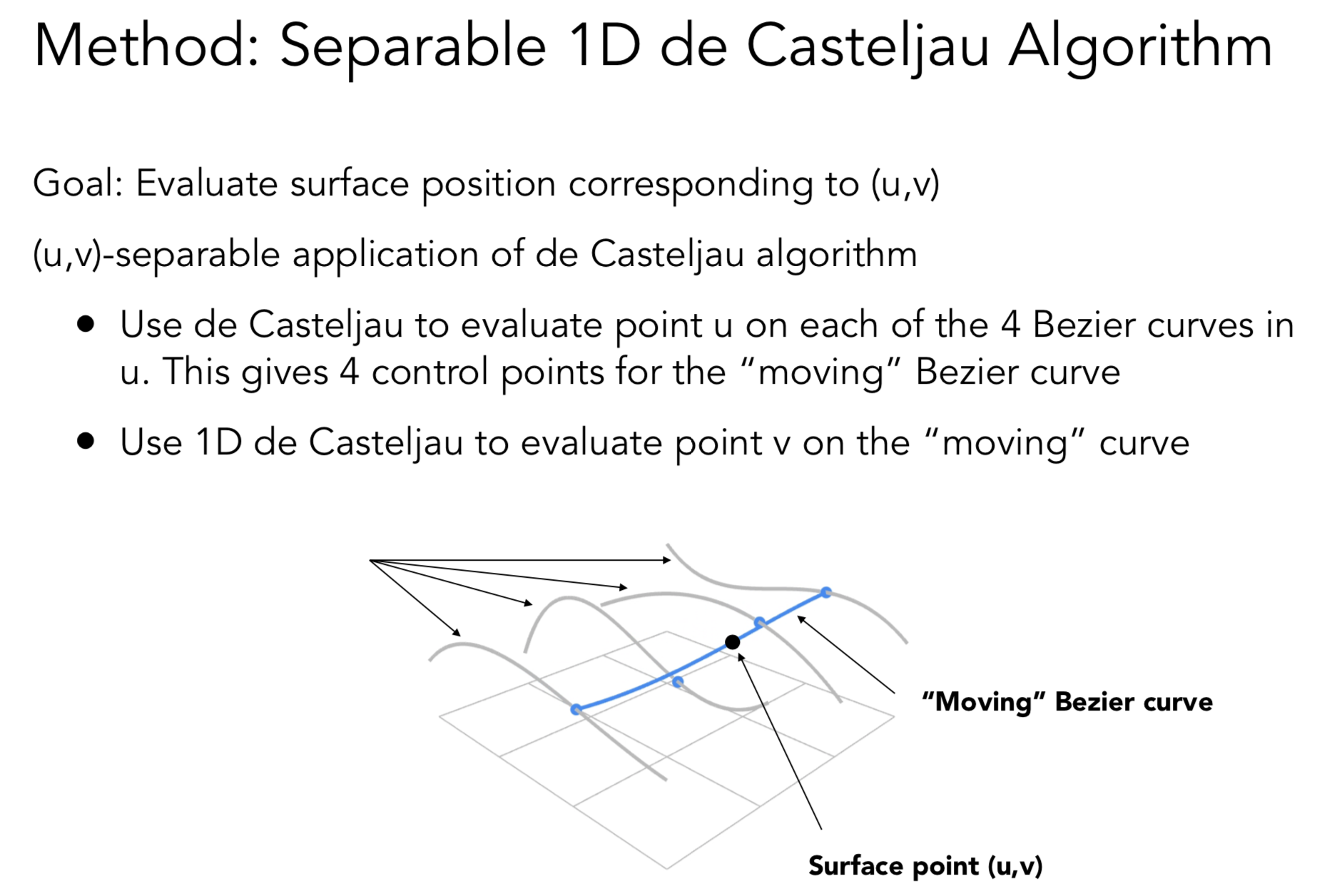
相当于 x 方向 和 y 方向都有贝塞尔曲线. 总共 4 * 4 = 16 个点来控制一小段曲面
贝塞尔曲面是显示表示, 因为是参数映射