- Scale
- Reflection Matrix
- Shear Matrix
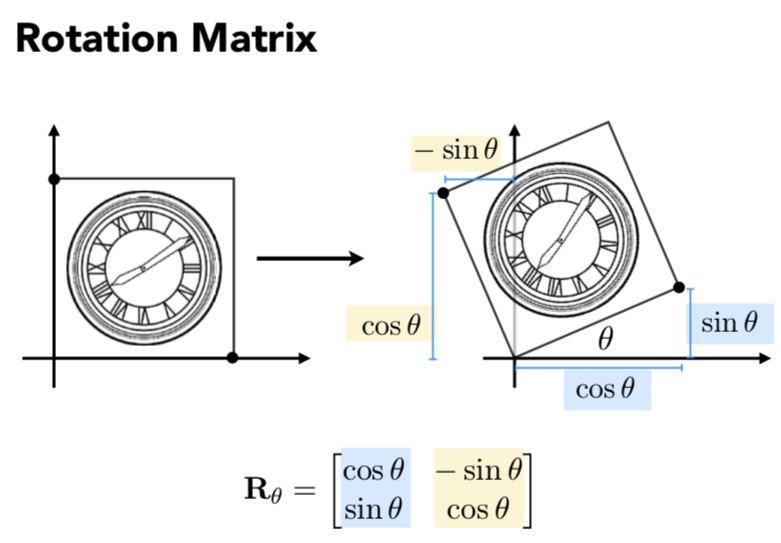
- Rotation Matrix
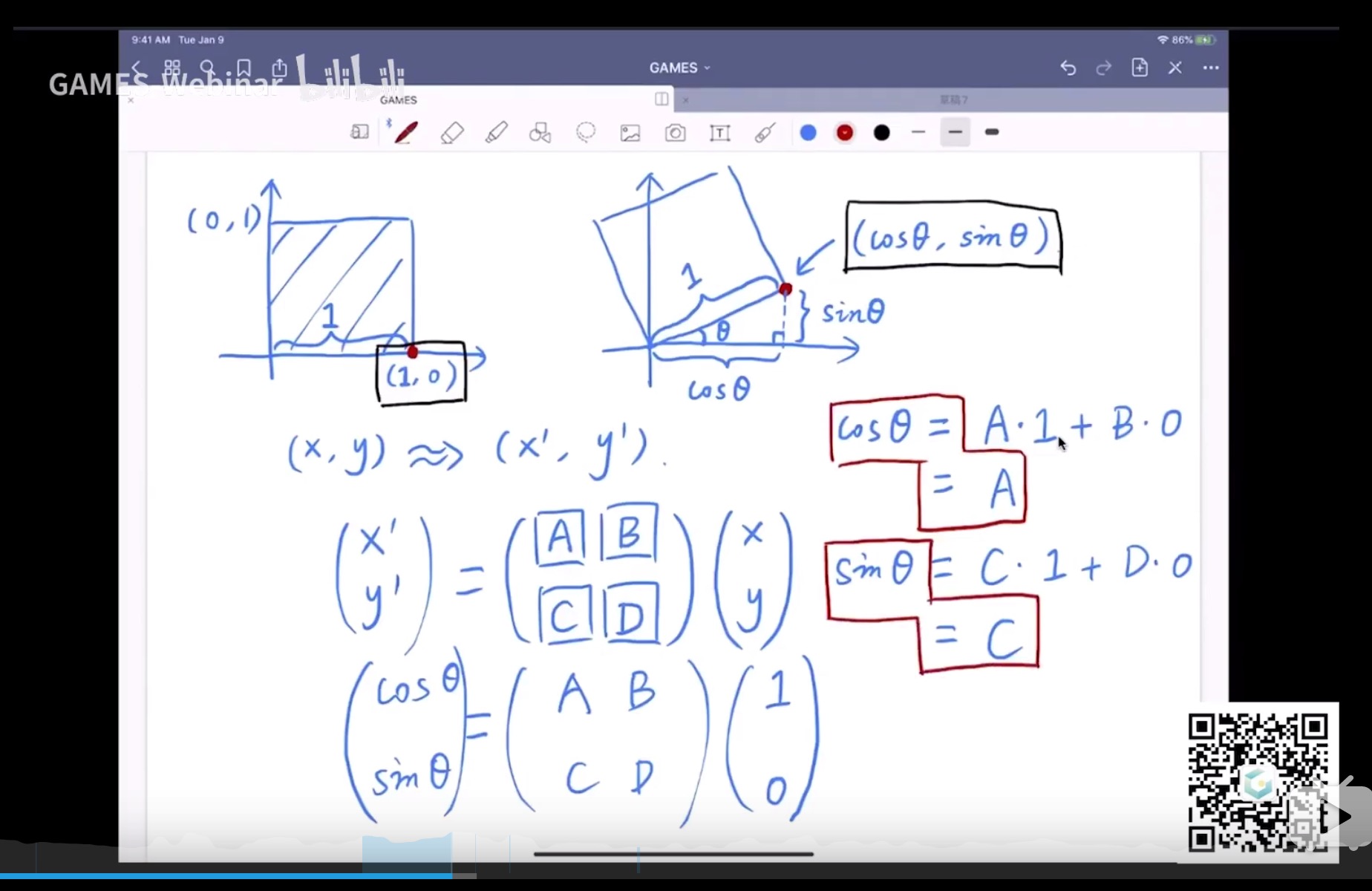
旋转矩阵的推导
先考虑特殊点 (1, 0) 可以得到 A 和 C 之后在考虑特殊点(0, 1) 可以推算到 B D
这些变换都可以写成一种线性组合,
简而言之,齐次坐标就是用N+1维来代表N维坐标
PS: 齐次坐标可让包括无穷远点的点坐标以有限坐标表示
考虑到 ponit + point 的运算(这样w 分量就是2了), 于是又扩展了齐次坐标的定义
PS 对于向量(x, y, z, w), 只要 w !=0 就认为所在三维坐标空间中的点是(x/w, y/w, z/w)
PS 关于齐次坐标向量和点的区别
在齐次坐标中, 对于点新增的维度值是 1. 而对于向量, 新增的维度值是0
向量平移要满足不变性, 也就是说一个向量(x, y) 在平移后, 仍然是(x, y)
所以, 向量新增的维度应该是0 我们把平移矩阵作用在这个新增了一个维度的向量之后发现, 果然结果仍是(x, y, 0)
并且, 根据 point - point = vector 向量的新增的这个维度也恰好是0.
也就是说, 齐次坐标新增的这个维度, 不影响现有的向量计算.
“仿射变换”就是:“线性变换”+“平移”
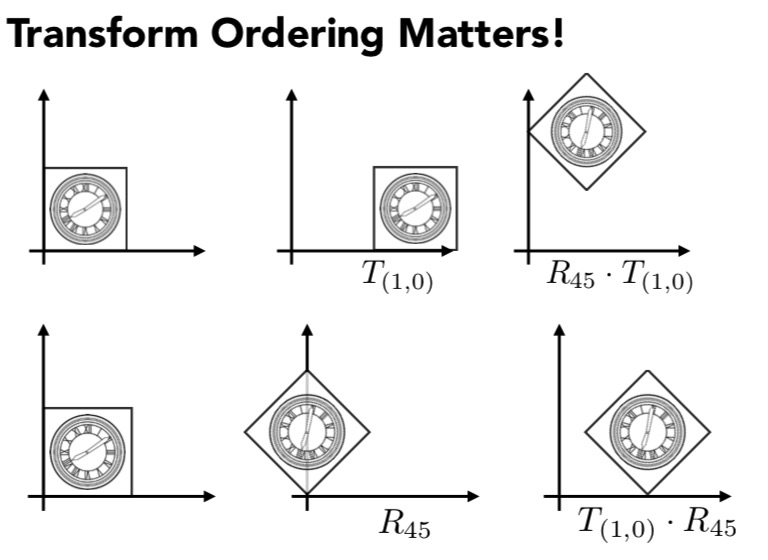
既然变换是用矩阵来表达, 所以多个变换就如同矩阵乘法, 顺序不可以调换. 因为矩阵乘法不满足交换律.
下面表示最先做 A1 变换, 再做 A2 变换 ...最后到An
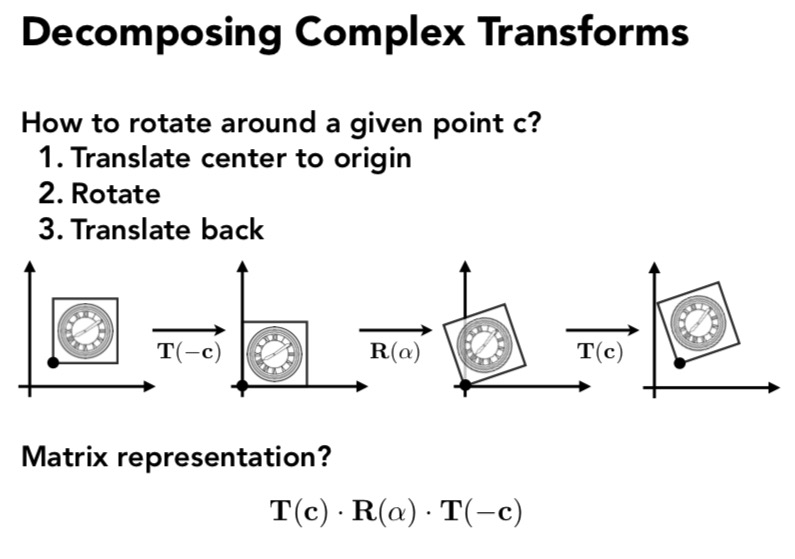
对于不在原点上物体做变换, 可以先移动它到原点, 变换之后再移动回去.