- 🌦 Intro
- 📂 Data preprocessing
- 🧹 Data Cleaning
- 📐 Feature engineering
- 🤖 Design the model
- 🕖 Train the model and validate it
- 🏆 Final Results
Implement an algorithm that performs next day rain prediction by training machine learning models on the target variable RainTomorrow.
The dataset contains about 10 years of daily weather observations from various locations in Australia.
RainTomorrow is the target variable to be predicted. It means - it rained the next day, this column is Yes if the rain that day was 1mm or more.
Available at: ./data/weatherAUS.csv
| Date | Location | MinTemp | MaxTemp | Rainfall | Evaporation | Sunshine | WindGustDir | WindGustSpeed | WindDir9am | WindDir3pm | WindSpeed9am | WindSpeed3pm | Humidity9am | Humidity3pm | Pressure9am | Pressure3pm | Cloud9am | Cloud3pm | Temp9am | Temp3pm | RainToday | RainTomorrow | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 99612 | 2009-03-10 | MountGambier | 12.0 | 27.6 | 0.0 | 4.2 | 4.9 | E | 37.0 | ESE | ESE | 20.0 | 11.0 | 82.0 | 36.0 | 1020.5 | 1017.5 | 7.0 | 6.0 | 16.5 | 27.3 | No | No |
RangeIndex: 145460 entries, 0 to 145459
Data columns (total 23 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Date 145460 non-null object
1 Location 145460 non-null object
2 MinTemp 143975 non-null float64
3 MaxTemp 144199 non-null float64
4 Rainfall 142199 non-null float64
5 Evaporation 82670 non-null float64
6 Sunshine 75625 non-null float64
7 WindGustDir 135134 non-null object
8 WindGustSpeed 135197 non-null float64
9 WindDir9am 134894 non-null object
10 WindDir3pm 141232 non-null object
11 WindSpeed9am 143693 non-null float64
12 WindSpeed3pm 142398 non-null float64
13 Humidity9am 142806 non-null float64
14 Humidity3pm 140953 non-null float64
15 Pressure9am 130395 non-null float64
16 Pressure3pm 130432 non-null float64
17 Cloud9am 89572 non-null float64
18 Cloud3pm 86102 non-null float64
19 Temp9am 143693 non-null float64
20 Temp3pm 141851 non-null float64
21 RainToday 142199 non-null object
22 RainTomorrow 142193 non-null object
dtypes: float64(16), object(7)
Wind directions are represented in Cardinal directions (e.g. N, S, SW,...). In order to make the dataset only with numbers, let's convert these directions into angles (degrees).
| WindGustDir | WindDir9am | WindDir3pm | |
|---|---|---|---|
| 0 | W | W | WNW |
weather_df['WindGustDir'] = weather_df['WindGustDir'].apply(lambda w: portolan.middle(str(w)) if str(w)!='nan' else w) weather_df['WindDir9am'] = weather_df['WindDir9am'].apply(lambda w: portolan.middle(str(w)) if str(w)!='nan' else w) weather_df['WindDir3pm'] = weather_df['WindDir3pm'].apply(lambda w: portolan.middle(str(w)) if str(w)!='nan' else w)
| WindGustDir | WindDir9am | WindDir3pm | |
|---|---|---|---|
| 0 | 270.0 | 270.0 | 292.5 |
weather_df.RainToday = weather_df.RainToday.map(dict(Yes=1, No=0)) weather_df.RainTomorrow = weather_df.RainTomorrow.map(dict(Yes=1, No=0))
In order to catch cyclic behaviors, we can feed the model with the day, month and year separately and allow it to perceive patterns related to seasons, for example.
weather_df['year'] = weather_df.Date.dt.year weather_df['month'] = weather_df.Date.dt.month weather_df['day'] = weather_df.Date.dt.day
The 'Location' column contains string values with the name of the location where the data was colected.
In order to convert the locations into numbers, we can use the coordinates for each one.
With this aproach, the column 'Location' becomes three new columns: latitude, longitude and altitude (all in decimal degrees).
Example: location Albury becomes latitude -36.0804766, longitude 146.9162795 and altitude 0.0.
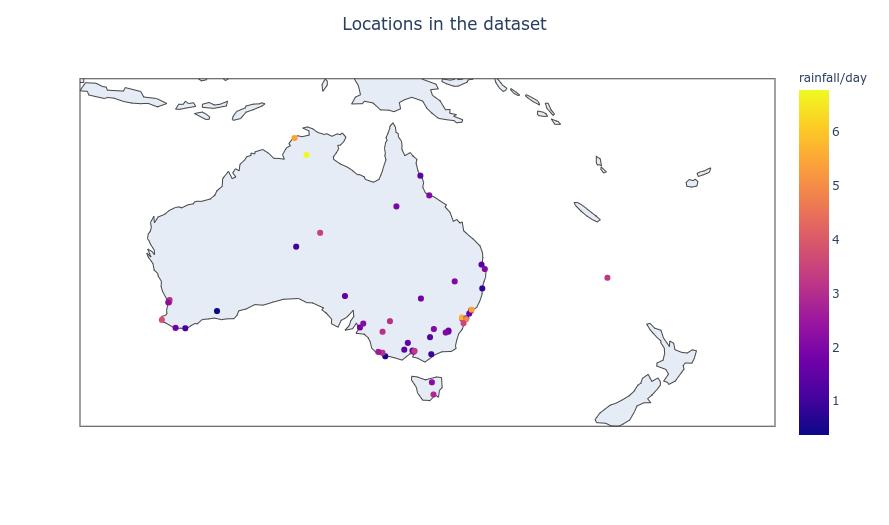
We could also plot the map of all the locations in the dataset, with its respective rainfall per day:
If there's no value in the target column, we cannot use it into our training or test set. So we can remove those rows from the dataset.
Before: Unique values in the RainTomorrow column: <IntegerArray> [0, 1, <NA>] Length: 3, dtype: Int64 Total number of rows: [ 145460 ] After: Unique values in the RainTomorrow column: <IntegerArray> [0, 1] Length: 2, dtype: Int64 Total number of rows: [ 142193 ] ( 3267 rows removed )
In this step, we use the 'mean' strategy to fill the missing values of the features.
imputer = SimpleImputer(missing_values=np.nan, strategy='mean') # transform the dataset weather_df_transformed = pd.DataFrame(imputer.fit_transform(weather_df)) weather_df_transformed.columns = weather_df.columns weather_df_transformed.index = weather_df.indexweather_df = weather_df_transformed
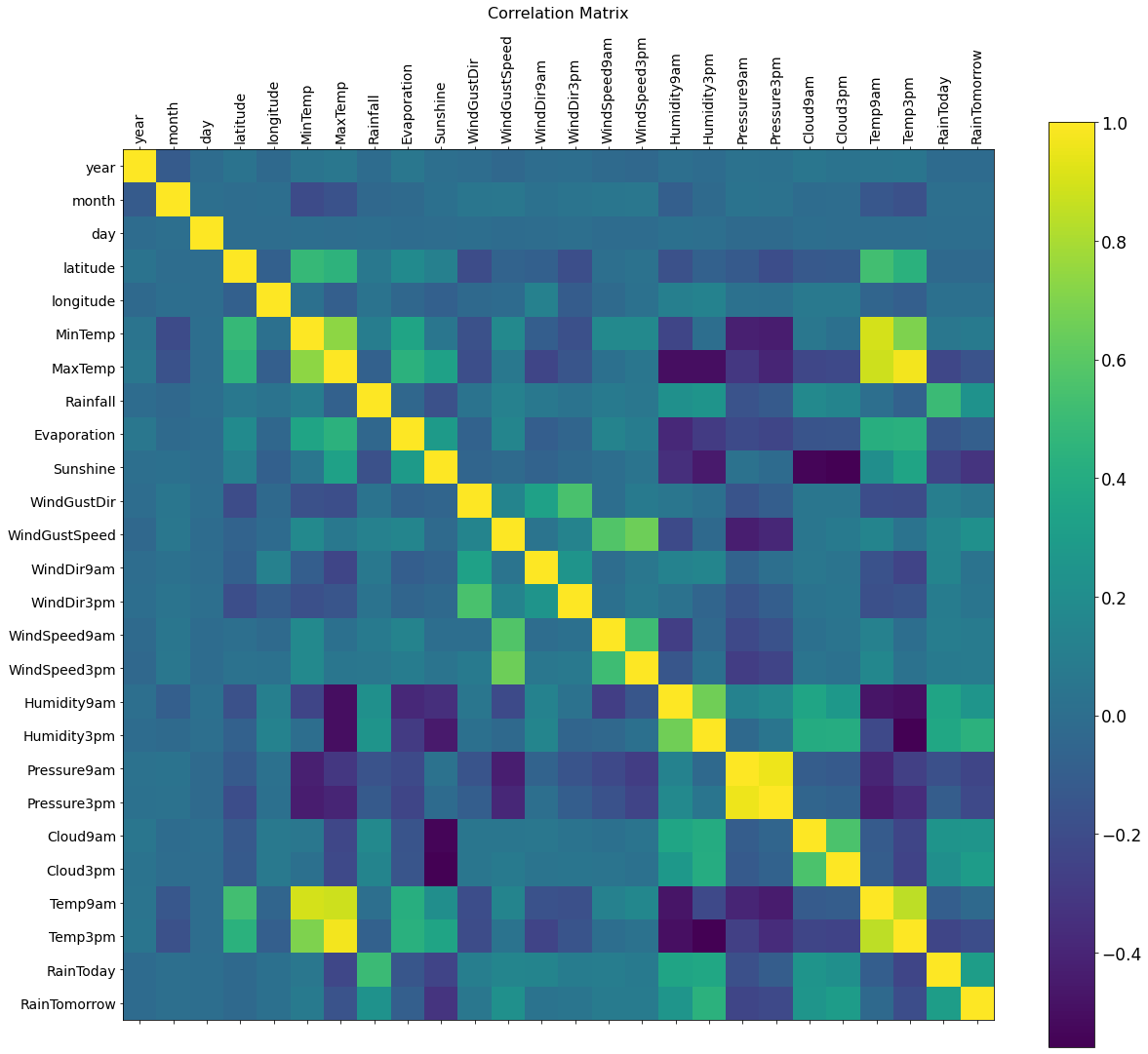
There are some correlation in the dataset. Enough to proceed with the work.
The MinMaxScaler puts the values between 0 and 1, which further improves the model performance.
scaler = MinMaxScaler(feature_range=(0, 1)) values = scaler.fit_transform(values)
X = features
Y = target
TARGET_NAME = 'RainTomorrow'
target_col_idx = weather_df.columns.get_loc(TARGET_NAME)X = values[:,0:target_col_idx].astype(float) Y = values[:,target_col_idx]
encoder = LabelEncoder() encoder.fit(Y) encoded_Y = encoder.transform(Y)
We want to predict a boolean value ('Yes' or 'No') for the target variable RainTomorrow. In this case, we need to use a classification model, istead of a regression model, which is used to predict real-world values (e.g. Rainfall).
def create_model(): model = Sequential(name='weather_guru') model.add(Dense(NEURONS_1, input_dim=NUM_FEATURES, activation='relu', name='dense_1')) model.add(Dense(NEURONS_2, activation='relu', name='dense_2')) model.add(Dense(1, activation='sigmoid', name='output')) adam_optmz = Adam(learning_rate=LEARNING_RATE) # Compile model model.compile(loss=LOSS_FUNCTION, optimizer=adam_optmz, metrics=['accuracy']) print(model.summary()) return modelestimators = [] estimators.append(('standardize', StandardScaler())) estimators.append(('mlp', KerasClassifier(build_fn = create_model, epochs = EPOCHS, batch_size = BATCH_SIZE, verbose = 1))) pipeline = Pipeline(estimators)
The number of epochs is the number of complete passes through the training dataset. The number 100 is arbitrary, chosen to improve the model accuracy and training time.
The size of a batch must be more than or equal to one and less than or equal to the number of samples in the training dataset. The number 1023 is also arbitrary, chosen to improve the model accuracy and training time.
The number of iterations used in the cross validation. The number 5 is arbitrary, chosen to reduce the time the validation takes.
Binary cross entropy compares each of the predicted probabilities to actual class output which can be either 0 or 1. The loss function 'binary_crossentropy' was chosen since the target variable is binary.
Learning rate used in the Adam optimizer. The value of 0.001 is arbitrary, chosen by trial and error, evaluating the model's improvements.
The number of neurons in the first hidden layer. The values 27 is arbitrary, chosen by trial and error, evaluating the model's improvements.
The number of neurons in the first hidden layer. The values 7 was chosen to 'force' the model to choose the most relevant features
We use the cross validation score to measure the accuracy of our model.
kfold = StratifiedKFold(n_splits=K_FOLD_SPLITS, shuffle=True)
%%time results = cross_val_score(pipeline, X, encoded_Y, cv=kfold)
See details of the training in the notebook:
'Accuracy: 85.73% (0.12%)'
This is the final result of model accuracy, after cross-validation scoring.
If necessary, we can change the topology or model settings to try to achieve better accuracy values.