envector

The envector library is a suite of tools written in Python to solve geographical position calculations. This is an open-source fork of the original nvector Python package based on the MATLAB n-vector toolbox.

Explanation of Intent

This is a Python package that will assist you in calculating the distance between two points anywhere on, above, or below the Earth's surface. This can also be between two, three, or many points. This is quite useful in many areas from logistics, tracking, navigation, data analytics, data science, and research. The calculations are simple and non-singular. Full accuracy is achieved for any global position (and for any distance).

Use Cases

A use case in logistics is when you need to recommend to your customers the closest facilities or store locations given an address or GPS coordinates. Your customers usually provide an address and you can convert that to GPS coordinates, or geographic location in latitude and longitude. Given this information, you need to recommend the closest locations and approximate distance in kilometers (km) or miles. You can implement the Haversine formula, which is a reasonable estimate if you are concerned with relatively short distances less than 100 km. However, you might meed to be aware of the difference in altitudes between two locations. On top of all that, the Haversine formula is not accurate for longer distances as the Earth is not exactly a sphere. You can properly account for all these issues using our envector package.

Another use case is for navigation and tracking. Imagine that you have a vehicle like a ship, airplane, or off-road vehicle on a fixed course. The vehicle has an unreliable and inaccurate GPS unit, and it is your job to ensure that the vehicle stays on course. This makes your job much harder if you want to minimize the trip duration and vehicle fuel to maximize the number of trips possible for the day. Fortunately, the envector package can help you 1) aggregate measurements to estimate the mean position, 2) interpolate the next expected position in a fixed time interval, and 3) determine if the vehicle is veering off-course by measuring the cross-track distance from the intended path.

These use cases and more are well supported by the envector package. We encourage you to check out the examples below to help you maximize the utility of envector.

Questions and Answers

If you are coming from the nvector package, these Q-and-A can quickly explain this package.

1. What is the difference between this package and nvector?

   • Virtually none! The envector package is a fork of nvector with mostly aesthetic changes.
   • No methods and functions have been removed, but documented deprecated methods in nvector will be removed.
   • If your Python software worked with nvector, then there is a good chance envector will also work. The caveats are that this package abandons Python2 and extends to Python3.9+ support.

2. Why did you call this package "envector"?

   • The name honors the original nvector Python package and the progenitor MATLAB n-vector toolbox. There are adaptations in other languages as noted in the nvector downloads page.
   • The names nvector and envector are homophones (pronounced the same), so the name invokes the original n-vector origin.

3. Why did you fork nvector?

   • Primarily because the nvector Python package is broken with NumPy version 2.
   • There is no indication that the situation will change.

4. What changes are there with from nvector?

   • The major difference is the namespace. Any place where your project have statements like:

     import nvector as nv
     from nvector import GeoPoint

     You would replace them:

     import envector as nv
     from envector import GeoPoint

   • The envector package is a Python3-only package as it embraces static typing in most cases.

   • Documentation is expanded in some cases.

   • The docstrings have been refactored to utilize the Napoleon docstring style.

5. When is the appropriate to switch to envector?

   • If your Python software must support NumPy version 2,
   • If your Python software also stops supporting Python versions after its end-of-life cycle.

6. How do I make the switch to envector?

   • If your project utilizes CPython3.9 through 3.12, inclusive, then you can simply change your requirements.txt, environment.yml, pyproject.toml, or setup.py file to specify envector.

     # requirements.txt format
     envector>=0
     

     # environment.yml format
     - pip:
       - envector>=0

     # pyproject.toml format
     # PEP 508 compliant
     [project]
     dependencies = [
         "envector>=0"
     ]
     
     # Poetry (not PEP 508 compliant)
     [tool.poetry.dependencies]
     envector = ">=0"

     # setup.py format
     install_requires=['envector>=0',
                       ...
                       ]

     • Your Python code will now need to import envector

   • If your project uses anything less than CPython3.9, then it depends on how your project is specified. If you are using pyproject.toml or setup.py, then the changes are relatively simple as shown below. The other common Anaconda environment.yml and requirements.txt formats require you to pick one depending on the Python version. For Python2 to 3.8, you cannot use envector.

     # pyproject.toml format
     # PEP 508 compliant
     [project]
     dependencies = [
         "envector>=0; python_version >= '3.9'",
         "nvector>=0; python_version < '3.9'",
     ]
     
     # Poetry (not PEP 508 compliant)
     [tool.poetry.dependencies]
     envector = { version = ">=0", python = ">=3.9" }
     nvector = { version = ">=0", python = "<3.9" }

     # setup.py format
     install_requires=['envector>=0; python_version >= "3.9"',
                       'nvector>=0; python_version < "3.9"',
                       ...
                       ]

     • Your Python code will now need to try and import envector or nvector in a try-except block.

           # Code block to import either nvector or envector
           try:
               import nvector as nv
           except (ImportError,):
               import envector as nv

Technical Description

In this library, we represent position with an "n-vector", which is the normal vector to the Earth model (the same reference ellipsoid that is used for latitude and longitude). When using n-vector, all Earth-positions are treated equally, and there is no need to worry about singularities or discontinuities. An additional benefit with using n-vector is that many position calculations can be solved with simple vector algebra (e.g. dot product and cross product).

Converting between n-vector and latitude/longitude is unambiguous and easy using the provided functions.

n_E is n-vector in the program code, while in documents we use nE. E denotes an Earth-fixed coordinate frame, and it indicates that the three components of n-vector are along the three axes of E. More details about the notation and reference frames can be found in the documentation.

Documentation and code

Official documentation:

http://www.navlab.net/nvector/

http://envector.readthedocs.io/en/latest/

Kenneth Gade (2010):

A Nonsingular Horizontal Position Representation, The Journal of Navigation, Volume 63, Issue 03, pp 395-417, July 2010.

Bleeding edge: https://github.com/mhogan-nwra/envector.

Official releases available at: http://pypi.python.org/pypi/envector.

Original/precursor package nvector at: http://pypi.python.org/pypi/nvector.

Install envector

If you have pip installed and are online, then simply type:

$ pip install envector

to get the latest stable version. Using pip also has the advantage that all requirements are automatically installed.

You can download nvector and all dependencies to a folder "pkg", by the following:

$ pip install --download=pkg envector

To install the downloaded envector, just type:

$ pip install --no-index --find-links=pkg envector

Verifying installation

To verify that envector can be seen by Python, type python from your shell. Then at the Python prompt, try to import envector:

>>> import envector as nv
>>> print(nv.__version__)
0.3.1

To test if the toolbox is working correctly paste the following in an interactive python session:

import envector as nv
nv.test('--doctest-modules')

Getting Started with Examples

Below the object-oriented solution to some common geodesic problems are given. In the first example the functional solution is also given. The functional solutions to the remaining problems can be found in the functional examples section of the tutorial.

Example 1: "A and B to delta"

Given two positions, A and B as latitudes, longitudes and depths relative to Earth, E.

Find the exact vector between the two positions, given in meters north, east, and down, and find the direction (azimuth) to B, relative to north. Assume WGS-84 ellipsoid. The given depths are from the ellipsoid surface. Use position A to define north, east, and down directions. (Due to the curvature of Earth and different directions to the North Pole, the north, east, and down directions will change (relative to Earth) for different places. Position A must be outside the poles for the north and east directions to be defined.)

Solution:

>>> import numpy as np
>>> import envector as nv
>>> wgs84 = nv.FrameE(name='WGS84')
>>> pointA = wgs84.GeoPoint(latitude=1, longitude=2, z=3, degrees=True)
>>> pointB = wgs84.GeoPoint(latitude=4, longitude=5, z=6, degrees=True)

Step1: Find p_AB_N (delta decomposed in N).

>>> p_AB_N = pointA.delta_to(pointB)
>>> x, y, z = p_AB_N.pvector.ravel()
>>> 'Ex1: delta north, east, down = {0:8.2f}, {1:8.2f}, {2:8.2f}'.format(x, y, z)
'Ex1: delta north, east, down = 331730.23, 332997.87, 17404.27'

Step2: Also find the direction (azimuth) to B, relative to north:

>>> 'azimuth = {0:4.2f} deg'.format(p_AB_N.azimuth_deg)
'azimuth = 45.11 deg'
>>> 'elevation = {0:4.2f} deg'.format(p_AB_N.elevation_deg)
'elevation = 2.12 deg'
>>> 'distance = {0:4.2f} m'.format(p_AB_N.length)
'distance = 470356.72 m'

Functional Solution:

>>> import numpy as np
>>> import envector as nv
>>> from envector import rad, deg

>>> lat_EA, lon_EA, z_EA = rad(1), rad(2), 3
>>> lat_EB, lon_EB, z_EB = rad(4), rad(5), 6

Step1: Convert to n-vectors:

>>> n_EA_E = nv.lat_lon2n_E(lat_EA, lon_EA)
>>> n_EB_E = nv.lat_lon2n_E(lat_EB, lon_EB)

Step2: Find p_AB_E (delta decomposed in E).WGS-84 ellipsoid is default:

>>> p_AB_E = nv.n_EA_E_and_n_EB_E2p_AB_E(n_EA_E, n_EB_E, z_EA, z_EB)

Step3: Find R_EN for position A:

>>> R_EN = nv.n_E2R_EN(n_EA_E)

Step4: Find p_AB_N (delta decomposed in N).

>>> p_AB_N = np.dot(R_EN.T, p_AB_E).ravel()
>>> x, y, z = p_AB_N
>>> 'Ex1: delta north, east, down = {0:8.2f}, {1:8.2f}, {2:8.2f}'.format(x, y, z)
'Ex1: delta north, east, down = 331730.23, 332997.87, 17404.27'

Step5: Also find the direction (azimuth) to B, relative to north:

>>> azimuth = np.arctan2(y, x)
>>> 'azimuth = {0:4.2f} deg'.format(deg(azimuth))
'azimuth = 45.11 deg'

>>> distance = np.linalg.norm(p_AB_N)
>>> elevation = np.arcsin(z / distance)
>>> 'elevation = {0:4.2f} deg'.format(deg(elevation))
'elevation = 2.12 deg'

>>> 'distance = {0:4.2f} m'.format(distance)
'distance = 470356.72 m'

See also

Example 1 at www.navlab.net

Example 2: "B and delta to C"

A radar or sonar attached to a vehicle B (Body coordinate frame) measures the distance and direction to an object C. We assume that the distance and two angles (typically bearing and elevation relative to B) are already combined to the vector p_BC_B (i.e. the vector from B to C, decomposed in B). The position of B is given as n_EB_E and z_EB, and the orientation (attitude) of B is given as R_NB (this rotation matrix can be found from roll/pitch/yaw by using zyx2R).

Find the exact position of object C as n-vector and depth ( n_EC_E and z_EC ), assuming Earth ellipsoid with semi-major axis a and flattening f. For WGS-72, use a = 6 378 135 m and f = 1/298.26.

Solution:

>>> import numpy as np
>>> import envector as nv
>>> wgs72 = nv.FrameE(name='WGS72')
>>> wgs72 = nv.FrameE(a=6378135, f=1.0/298.26)

Step 1: Position and orientation of B is given 400m above E:

>>> n_EB_E = wgs72.Nvector(nv.unit([[1], [2], [3]]), z=-400)
>>> frame_B = nv.FrameB(n_EB_E, yaw=10, pitch=20, roll=30, degrees=True)

Step 2: Delta BC decomposed in B

>>> p_BC_B = frame_B.Pvector(np.r_[3000, 2000, 100].reshape((-1, 1)))

Step 3: Decompose delta BC in E

>>> p_BC_E = p_BC_B.to_ecef_vector()

Step 4: Find point C by adding delta BC to EB

>>> p_EB_E = n_EB_E.to_ecef_vector()
>>> p_EC_E = p_EB_E + p_BC_E
>>> pointC = p_EC_E.to_geo_point()

>>> lat, lon, z = pointC.latlon_deg
>>> msg = 'Ex2: PosC: lat, lon = {:4.4f}, {:4.4f} deg,  height = {:4.2f} m'
>>> msg.format(lat, lon, -z)
'Ex2: PosC: lat, lon = 53.3264, 63.4681 deg,  height = 406.01 m'

See also

Example 2 at www.navlab.net

Example 3: "ECEF-vector to geodetic latitude"

Position B is given as an "ECEF-vector" p_EB_E (i.e. a vector from E, the center of the Earth, to B, decomposed in E). Find the geodetic latitude, longitude and height (latEB, lonEB and hEB), assuming WGS-84 ellipsoid.

Solution:

>>> import numpy as np
>>> import envector as nv
>>> wgs84 = nv.FrameE(name='WGS84')
>>> position_B = 6371e3 * np.vstack((0.9, -1, 1.1))  # m
>>> p_EB_E = wgs84.ECEFvector(position_B)
>>> pointB = p_EB_E.to_geo_point()

>>> lat, lon, z = pointB.latlon_deg
>>> 'Ex3: Pos B: lat, lon = {:4.4f}, {:4.4f} deg, height = {:9.3f} m'.format(lat, lon, -z)
'Ex3: Pos B: lat, lon = 39.3787, -48.0128 deg, height = 4702059.834 m'

See also

Example 3 at www.navlab.net

Example 4: "Geodetic latitude to ECEF-vector"

Geodetic latitude, longitude and height are given for position B as latEB, lonEB and hEB, find the ECEF-vector for this position, p_EB_E.

Solution:

>>> import envector as nv
>>> wgs84 = nv.FrameE(name='WGS84')
>>> pointB = wgs84.GeoPoint(latitude=1, longitude=2, z=-3, degrees=True)
>>> p_EB_E = pointB.to_ecef_vector()

>>> 'Ex4: p_EB_E = {} m'.format(p_EB_E.pvector.ravel().tolist())
'Ex4: p_EB_E = [6373290.277218279, 222560.20067473652, 110568.82718178593] m'

See also

Example 4 at www.navlab.net

Example 5: "Surface distance"

Find the surface distance sAB (i.e. great circle distance) between two positions A and B. The heights of A and B are ignored, i.e. if they don't have zero height, we seek the distance between the points that are at the surface of the Earth, directly above/below A and B. The Euclidean distance (chord length) dAB should also be found. Use Earth radius 6371e3 m. Compare the results with exact calculations for the WGS-84 ellipsoid.

Solution for a sphere:

>>> import numpy as np
>>> import envector as nv
>>> frame_E = nv.FrameE(a=6371e3, f=0)
>>> positionA = frame_E.GeoPoint(latitude=88, longitude=0, degrees=True)
>>> positionB = frame_E.GeoPoint(latitude=89, longitude=-170, degrees=True)

>>> s_AB, azia, azib = positionA.distance_and_azimuth(positionB)
>>> p_AB_E = positionB.to_ecef_vector() - positionA.to_ecef_vector()
>>> d_AB = p_AB_E.length

>>> msg = 'Ex5: Great circle and Euclidean distance = {}'
>>> msg = msg.format('{:5.2f} km, {:5.2f} km')
>>> msg.format(s_AB / 1000, d_AB / 1000)
'Ex5: Great circle and Euclidean distance = 332.46 km, 332.42 km'

Alternative sphere solution:

>>> path = nv.GeoPath(positionA, positionB)
>>> s_AB2 = path.track_distance(method='greatcircle')
>>> d_AB2 = path.track_distance(method='euclidean')
>>> msg.format(s_AB2 / 1000, d_AB2 / 1000)
'Ex5: Great circle and Euclidean distance = 332.46 km, 332.42 km'

Exact solution for the WGS84 ellipsoid:

>>> wgs84 = nv.FrameE(name='WGS84')
>>> point1 = wgs84.GeoPoint(latitude=88, longitude=0, degrees=True)
>>> point2 = wgs84.GeoPoint(latitude=89, longitude=-170, degrees=True)
>>> s_12, azi1, azi2 = point1.distance_and_azimuth(point2)

>>> p_12_E = point2.to_ecef_vector() - point1.to_ecef_vector()
>>> d_12 = p_12_E.length
>>> msg = 'Ellipsoidal and Euclidean distance = {:5.2f} km, {:5.2f} km'
>>> msg.format(s_12 / 1000, d_12 / 1000)
'Ellipsoidal and Euclidean distance = 333.95 km, 333.91 km'

See also

Example 5 at www.navlab.net

Example 6 "Interpolated position"

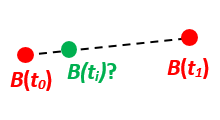
Given the position of B at time t0 and t1, n_EB_E(t0) and n_EB_E(t1).

Find an interpolated position at time ti, n_EB_E(ti). All positions are given as n-vectors.

Solution:

>>> import envector as nv
>>> wgs84 = nv.FrameE(name='WGS84')
>>> n_EB_E_t0 = wgs84.GeoPoint(89, 0, degrees=True).to_nvector()
>>> n_EB_E_t1 = wgs84.GeoPoint(89, 180, degrees=True).to_nvector()
>>> path = nv.GeoPath(n_EB_E_t0, n_EB_E_t1)

>>> t0 = 10.
>>> t1 = 20.
>>> ti = 16.  # time of interpolation
>>> ti_n = (ti - t0) / (t1 - t0) # normalized time of interpolation

>>> g_EB_E_ti = path.interpolate(ti_n).to_geo_point()

>>> lat_ti, lon_ti, z_ti = g_EB_E_ti.latlon_deg
>>> msg = 'Ex6, Interpolated position: lat, lon = {:2.1f} deg, {:2.1f} deg'
>>> msg.format(lat_ti, lon_ti)
'Ex6, Interpolated position: lat, lon = 89.8 deg, 180.0 deg'

Vectorized solution:

>>> t = np.array([10, 20])
>>> nvectors = wgs84.GeoPoint([89, 89], [0, 180], degrees=True).to_nvector()
>>> nvectors_i = nvectors.interpolate(ti, t, kind='linear')
>>> lati, loni, zi = nvectors_i.to_geo_point().latlon_deg
>>> msg.format(lat_ti, lon_ti)
'Ex6, Interpolated position: lat, lon = 89.8 deg, 180.0 deg'

See also

Example 6 at www.navlab.net

Example 7: "Mean position"

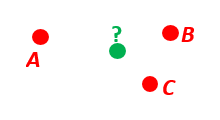
Three positions A, B, and C are given as n-vectors n_EA_E, n_EB_E, and n_EC_E. Find the mean position, M, given as n_EM_E. Note that the calculation is independent of the depths of the positions.

Solution:

>>> import envector as nv
>>> points = nv.GeoPoint(latitude=[90, 60, 50],
...                      longitude=[0, 10, -20], degrees=True)
>>> nvectors = points.to_nvector()
>>> n_EM_E = nvectors.mean()
>>> g_EM_E = n_EM_E.to_geo_point()
>>> lat, lon = g_EM_E.latitude_deg, g_EM_E.longitude_deg
>>> msg = 'Ex7: Pos M: lat, lon = {:4.4f}, {:4.4f} deg'
>>> msg.format(lat, lon)
'Ex7: Pos M: lat, lon = 67.2362, -6.9175 deg'

See also

Example 7 at www.navlab.net

Example 8: "A and azimuth/distance to B"

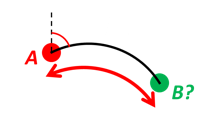
We have an initial position A, direction of travel given as an azimuth (bearing) relative to north (clockwise), and finally the distance to travel along a great circle given as sAB. Use Earth radius 6371e3 m to find the destination point B.

In geodesy this is known as "The first geodetic problem" or "The direct geodetic problem" for a sphere, and we see that this is similar to Example 2, but now the delta is given as an azimuth and a great circle distance. ("The second/inverse geodetic problem" for a sphere is already solved in Examples 1 and 5.)

Exact solution:

>>> import numpy as np
>>> import envector as nv
>>> frame = nv.FrameE(a=6371e3, f=0)
>>> pointA = frame.GeoPoint(latitude=80, longitude=-90, degrees=True)
>>> pointB, azimuthb = pointA.displace(distance=1000, azimuth=200, degrees=True)
>>> lat, lon = pointB.latitude_deg, pointB.longitude_deg

>>> msg = 'Ex8, Destination: lat, lon = {:4.4f} deg, {:4.4f} deg'
>>> msg.format(lat, lon)
'Ex8, Destination: lat, lon = 79.9915 deg, -90.0177 deg'

>>> np.allclose(azimuthb, -160.01742926820506)
True

Greatcircle solution:

>>> pointB2, azimuthb = pointA.displace(distance=1000,
...                                     azimuth=200,
...                                     degrees=True,
...                                     method='greatcircle')
>>> lat2, lon2 = pointB2.latitude_deg, pointB.longitude_deg
>>> msg.format(lat2, lon2)
'Ex8, Destination: lat, lon = 79.9915 deg, -90.0177 deg'

>>> np.allclose(azimuthb, -160.0174292682187)
True

See also

Example 8 at www.navlab.net

Example 9: "Intersection of two paths"

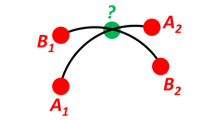
Define a path from two given positions (at the surface of a spherical Earth), as the great circle that goes through the two points.

Path A is given by A1 and A2, while path B is given by B1 and B2.

Find the position C where the two great circles intersect.

Solution:

>>> import envector as nv
>>> pointA1 = nv.GeoPoint(10, 20, degrees=True)
>>> pointA2 = nv.GeoPoint(30, 40, degrees=True)
>>> pointB1 = nv.GeoPoint(50, 60, degrees=True)
>>> pointB2 = nv.GeoPoint(70, 80, degrees=True)
>>> pathA = nv.GeoPath(pointA1, pointA2)
>>> pathB = nv.GeoPath(pointB1, pointB2)

>>> pointC = pathA.intersect(pathB)
>>> pointC = pointC.to_geo_point()
>>> lat, lon = pointC.latitude_deg, pointC.longitude_deg
>>> msg = 'Ex9, Intersection: lat, lon = {:4.4f}, {:4.4f} deg'
>>> msg.format(lat, lon)
'Ex9, Intersection: lat, lon = 40.3186, 55.9019 deg'

Check that PointC is not between A1 and A2 or B1 and B2:

>>> pathA.on_path(pointC)
False
>>> pathB.on_path(pointC)
False

Check that PointC is on the great circle going through path A and path B:

>>> pathA.on_great_circle(pointC)
True
>>> pathB.on_great_circle(pointC)
True

See also

Example 9 at www.navlab.net

Example 10: "Cross track distance"

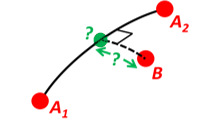
Path A is given by the two positions A1 and A2 (similar to the previous example).

Find the cross track distance sxt between the path A (i.e. the great circle through A1 and A2) and the position B (i.e. the shortest distance at the surface, between the great circle and B).

Also find the Euclidean distance dxt between B and the plane defined by the great circle. Use Earth radius 6371e3.

Finally, find the intersection point on the great circle and determine if it is between position A1 and A2.

Solution:

>>> import numpy as np
>>> import envector as nv
>>> frame = nv.FrameE(a=6371e3, f=0)
>>> pointA1 = frame.GeoPoint(0, 0, degrees=True)
>>> pointA2 = frame.GeoPoint(10, 0, degrees=True)
>>> pointB = frame.GeoPoint(1, 0.1, degrees=True)
>>> pathA = nv.GeoPath(pointA1, pointA2)

>>> s_xt = pathA.cross_track_distance(pointB, method='greatcircle')
>>> d_xt = pathA.cross_track_distance(pointB, method='euclidean')

>>> val_txt = '{:4.2f} km, {:4.2f} km'.format(s_xt/1000, d_xt/1000)
>>> 'Ex10: Cross track distance: s_xt, d_xt = {}'.format(val_txt)
'Ex10: Cross track distance: s_xt, d_xt = 11.12 km, 11.12 km'

>>> pointC = pathA.closest_point_on_great_circle(pointB)
>>> np.allclose(pathA.on_path(pointC), True)
True

See also

Example 10 at www.navlab.net

Acknowledgements

The nvector package for Python was written by Per A. Brodtkorb at FFI (The Norwegian Defence Research Establishment) based on the nvector toolbox for Matlab written by the navigation group at FFI. The nvector.core and nvector.rotation module is a vectorized reimplementation of the matlab nvector toolbox while the nvector.objects module is a new easy to use object oriented user interface to the nvector core functionality documented in [GB20].

Most of the content is based on the article by K. Gade [Gad10].

Thus this article should be cited in publications using this page or downloaded program code.

However, if you use any of the FrameE.direct, FrameE.inverse, GeoPoint.distance_and_azimuth or GeoPoint.displace methods you should also cite the article by Karney [Kar13] because these methods call Karney's geographiclib library to do the calculations.

References

[Gad10]

K. Gade, A Nonsingular Horizontal Position Representation, J. Navigation, 63(3):395-417, 2010.

[Kar13]

C.F.F. Karney. Algorithms for geodesics. J. Geodesy, 87(1):43-55, 2013.

[GB20]

K. Gade and P.A. Brodtkorb, Nvector Documentation for Python, 2020.