Example codes for my blog post: Understanding the EM Algorithm.
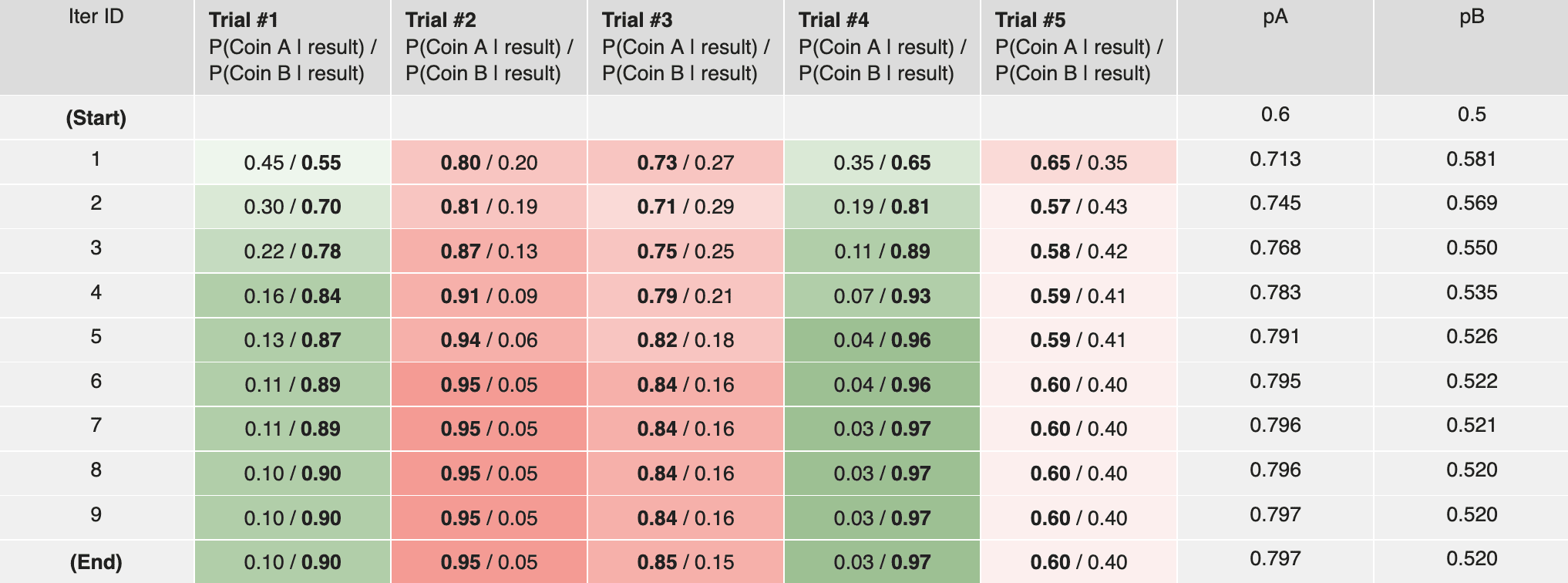
Find the probabilities of two coins A and B, given 5 coin tossing trials with missing information:
| Trial ID | Coin | Result | #heads / #tails |
|---|---|---|---|
| #1 | Unknown | HTTTHHTHTH | 5/5 |
| #2 | Unknown | HHHHTHHHHH | 9/1 |
| #3 | Unknown | HTHHHHHTHH | 8/2 |
| #4 | Unknown | HTHTTTHHTT | 4/6 |
| #5 | Unknown | THHHTHHHTH | 7/3 |
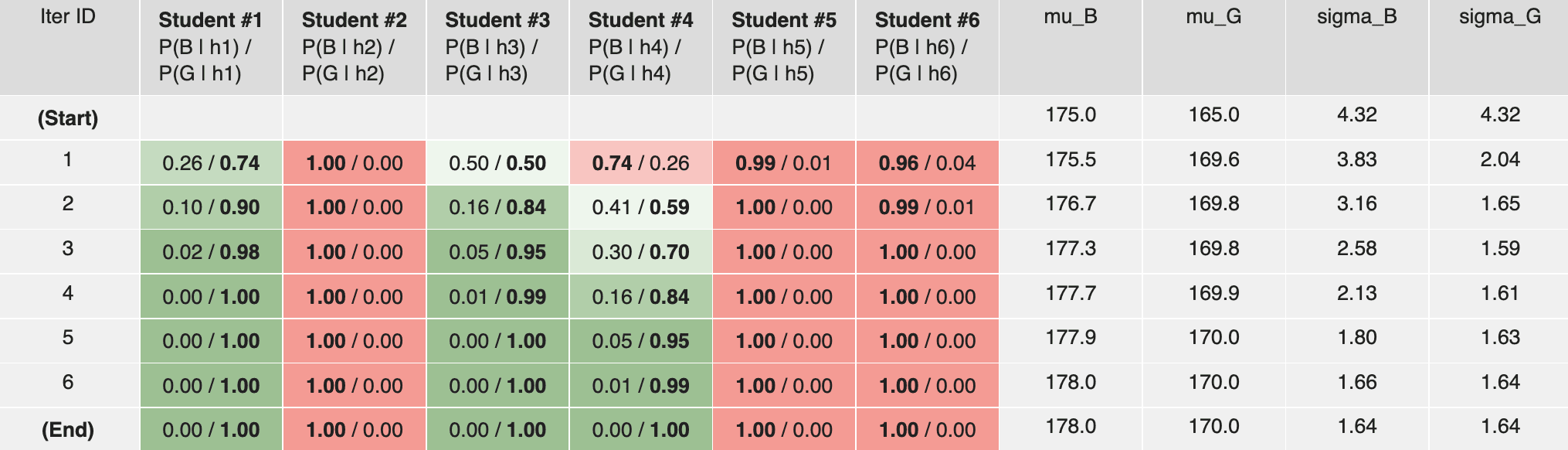
Infer the gender of 6 students given their heights (Note: in real life, inferring one's gender based on their height might be a bad idea. This example is for educational purposes only):
| Student ID | Gender | Height (cm) |
|---|---|---|
| #1 | Unknown | 168 |
| #2 | Unknown | 180 |
| #3 | Unknown | 170 |
| #4 | Unknown | 172 |
| #5 | Unknown | 178 |
| #6 | Unknown | 176 |
Distributed under the MIT License. See LICENSE for more information.
@mistylight - mistylight.cs@gmail.com
[1] What is the expectation maximization algorithm? Chuong B Do, Serafim Batzoglou. Nature, 2008. [paper]
[2] Expectation Maximization. Benjamin Bray. UMich EECS 545: Machine Learning course notes, 2016. [course notes]
[3] The EM algorithm. Tengyu Ma, Andrew Ng. Stanford CS 229: Machine Learning course notes, 2019. [course notes]
[4] Bayesian networks: EM algorithm. Stanford CS 221: Artificial Intelligence: Principles and Techniques slides, 2021. [slides]
[5] 如何感性地理解EM算法?工程师milter. 简书, 2017. [blog post]
[6] Coin Flipping and EM. Karl Rosaen, chansoo. UMich EECS 545: Machine Learning Materials. [Jupyter Notebook]