All the pain you feel it during and self developing he will go way one day after you see the result for your hard work. you have to know how much you will face obstacles, ups and downs during your journy is reflect to how much you learn new thing and your skills developed.
on other hand suffring is stand for pain wothout goals,dreams,no aspiration

- O(1)"Constant algorithm" O(1) describes an algorithm that will always execute in the same time (or space) regardless of the size of the input data set.
bool IsFirstElementNull(IList<String> elements)
{
return elements[0] == null;
}
- O(N) "linear algorithm" O(N) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set.also big O notation will always assume the upper limit where the algorithm will perform the maximum number of iterations.
bool ContainsValue(IEnumerable<string> elements, string value)
{
foreach (var element in elements)
{
if (element == value) return true;
}
return false;
}
- O(N²) "Polynmical Algorithm" O(N²) represents an algorithm whose performance is directly proportional to the square of the size of the input data set.
bool ContainsDuplicates(IList<string> elements)
{
for (var outer = 0; outer < elements.Count; outer++)
{
for (var inner = 0; inner < elements.Count; inner++)
{
// Don't compare with self
if (outer == inner) continue;
if (elements[outer] == elements[inner]) return true;
}
}
return false;
}
- O(2^N) "exponential Algorithm" O(2^N) denotes an algorithm whose growth doubles with each addition to the input data set. The growth curve of an O(2^N) function is exponential — starting off very shallow, then rising meteorically.
int Fibonacci(int number)
{
if (number <= 1) return number;
return Fibonacci(number - 2) + Fibonacci(number - 1);
}
🎉 100% fact in python 🎉
- names refer to values:
makes the name refer to that value so for instance when we execute
x=23 #23 is an integer. print (x) #23 - many names can refer to one value:
x=23
y=x
print (y,x) #23
- Names are reassigned independently:
x=23
y=x
print (x) #23
x=12
print (y,x) #y=23 , x=12
- Values live until no references:
Python memory is managed dynamically which means that values exist until there are no more references
x="hello"
print (x) #hello
x="world"
print (x) #world now hello not references to x any more
- Assignment never copies:
nums=[1,2,3] #nums referring to a list [1,2,3]
other=nums #other referring to the same list
- Changes are visible through all names Mutable aliasing:
- Amutable value
- more than one name
- the value changes
- all names see the changes
nums=[1,2,3]
other=nums
nums.append(4)
print (other) #[1,2,3,4] !!!
- Immutable values cant alias Immutable type:ints,floats,strings,tuples
x="hello"
y=x #y= hello
x=x+"there" #x= hello there
- "Changine" is unclear
changing an int:rebinding
x=x+1
changing a list:mutating
nums.append(7)
can also rebind lists:
nums=nums+[7]
pov:can't mutate an int: ints are immutable
- Mutable and immutable are assigned the same
Assigned is the same for all values Aliasing can make it seem differences
- Assigment variants
x+=y
x=x+y #conceptually
x=x._iadd_(y) #actually
#pseudo-code!
class list:
def iadd(self,other):
self.extend(other)
return self
#there are the same:
num_list +=[4,5]
num_list.extend([4,5]):num_list=num_list
- references can be more than just names
list elements are references
nums=[1,2,3]
#imagine the list nums West as a row of boxes with numbers in them but really each of those boxes is itself a reference to a value and the integers
x=nums[1]
*Lots of different things are references
Object attributes List element Dict values(and keys!) Anything on the left side of an assigment
my_obj.attr=23
my_dict[key]=24
my_list[index]=25
my_obj.attr[key][index].attr="etc,etc"
- lots of things are assignments All of these assign to X
x=...
for x in ...
class x(...):
def x(...):
def fn(x):
import x
from ...import x
except ..as x:
with ...as x:
- For loops
for x in sequence:
something(x)
whats really happend is
for x in sequence[0] #is X is assigned the first element in the sequence
something(x)
for x in sequence[1] #is X is assigned the second element in the sequence
something(x)
... # and its the same for rest of the element
- Function arguments are assignments: The following code show that function call is that the actual arguments are assigned to the formal parameters
def func(x): #x=num
print(x)
return
num=17
func (num) #x=num
print(num)
the following code show that we can append avlaue twice:
def append_twice(a_list,val):
a_list.append(val)
a_list.append(val)
return
nums=[1,2,3]
append_twice(nums,7)
print(nums) #[1,2,3,7,7]
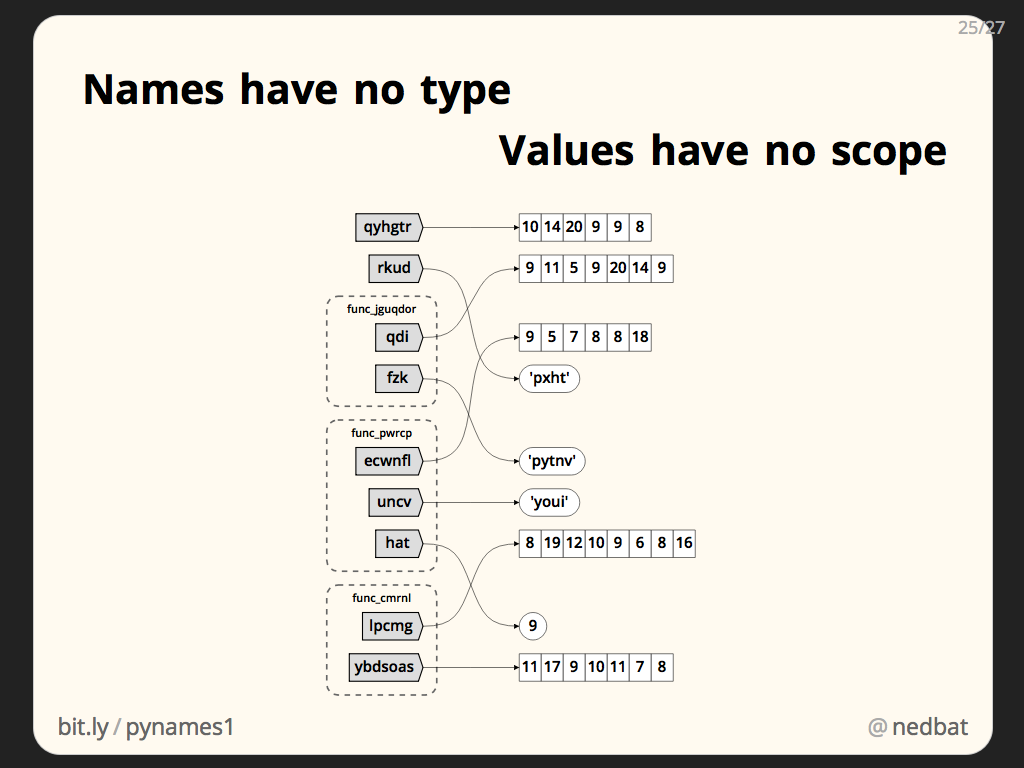
- Any name-> any value @any time: Dynamic typing, names have no types associated with them
x=12
x="hello"
x=[1,2,3]
x[1]="two"
- name have no type value have no scope python: