00_math_new_learend.md

다시 이해하게 된 것들

1. 고유분해 eigen-decomposition 중에서

분산행렬 X@X.T의 특징

• 어떠한 형태의 행렬이라도 분산행렬로 만들면 정방-대칭행렬이 된다.
  • (3x2) @ (2x3) = (3x3)
• 대칭행렬의 이차형식으로 부호를 판단하면 역행렬이 존재하는지, 풀랭크인지, 열벡터들이 선형독립인지 판단할 수 있다.
• 즉 풀랭크인 데이터 행렬일 수록 좋은 데이터라고 할때, 데이터의 좋고 나쁨을 판단하는 기준이 될 수 있다.

<어떤 행렬 X 가 풀랭크이면 이 행렬의 분산행렬의 역행렬은 항상 존재한다.>

행렬 X 가 풀랭크이면 분산행렬이 양의 정부호가 된다. 
분산행렬은 대칭행렬이므로 대칭행렬이 양의 정부호이면 고윳값이 모두 양수이다. 0은 존재하지 않는다.
이 대칭행렬이 행렬식은 모든 고윳값의 곱이므로 0이 아니다.
행렬식이 0이 아니므로 대칭행렬의 역행렬이 항상 존재한다.

<역행렬이 존재하는 대칭행렬은 항상 양의 정부호가 아니다.>

역행렬의 존재조건인 행렬식이 양수 또는 음수가 될 수 있다.
행렬식이 음수이면, 고윳값중에 한 개 이상이 음수이어야 한다.
대칭행렬과 고윳값의 부호정리에 의해서, 고윳값 중에 음수가 있다면 대칭행렬은 양의 정부호가 아니다.
그러므로 역행렬이 존재한다고 해서 항상 양의 정부호라고 할 수 없다.

고유분해의 성질 요약

• 데이터 분석에서 자주 사용됨

* 행렬 A는 N개의 고윳값-고유벡터를 가진다. (복소수인 경우와 중복인 경우를 포함)
* 행렬의 대각합은 모든 고윳값의 합과 같다.
* 행렬의 행렬식은 모든 고윳값의 곱과 같다.
* 행렬 A가 대칭행렬이면 실수 고윳값 N개를 가지며 고유벡터들이 서로 직교이다.
* 행렬 A가 대칭행렬이고 고윳값이 모두 양수이면 양의 정부호이고 역행렬이 존재한다. 역도 성립한다.
* 행렬 A가 어떤 행렬 X의 분산행렬이면 0 또는 양의 고윳값을 가진다.
* 행렬 X가 풀랭크이면 분산행렬은 역행렬이 존재한다.

2. 근사문제

• 임의의 벡터들과 거리가 가장 가까운 직선이나, 벡터공간을 찾는 문제

조건

• N개의 M차원 벡터 a1, a2, ..., aN 과 거리가 가장 가까운 직선의 단위벡터 w를 찾는다.
• 또는 서로 직교하는 K개의 벡터 w1, w2, ..., wK가 기저벡터인 벡터공간 V에 N개의 M차원 벡터를 투영시켰을때 가장 유사한 투영벡터들을 만드는 w1, w2, ...,wk를 찾는다.

접근법

• 벡터 ai와 직선 w와의 거리를 작게하는 조건을 만들고 이 조건을 만족하는 값을 찾는방법
  • 1차원 근사문제, 일반적 근사문제, k차원 근사문제
• 벡터 ai를 직선 w나 벡터공간의 기저벡터들에 각각 투영해서 만든 투영벡터가 기존의 벡터들을 행벡터로 갖는 행렬 A와 가장 비슷한 행렬 A'를 찾는방법
  • 랭크-1 근사문제, 랭크-K 근사문제

요약

• 근사문제의 핵심은 임의의 벡터들과 가장 유사한 직선이나, 벡터공간을 찾는 것이다.
• 이를 위해서 임의의 벡터들을 행렬로 만들고 벡터의 기하학적 표현원리들을 사용하여 직선이나 벡터공간과의 거리를 수식화 한다.
• 선형대수의 법칙들을 사용하여 임의의 벡터들과 직선 또는 벡터공간과의 거리를 최소화하거나, 투영벡터가 원래의 벡터와 가장 유사하게 만든다.
• 이러한 과정에 의해 임의의 벡터들을 행벡터로 갖는 행렬 A의 특이분해에 의해 생성된 가장 큰 K개의 특잇값과 이에 대응하는 오르쪽 특이벡터 K가 값이 된다는 것을 알 수 있다.
• 근사문제의 원리를 사용하여 PCA(주성분 분석) 분석을 할 수 있다.
  • 주성분 분석을 통하여 붓꽃의 크기, 주식 가격 변화, 집 값 변화, 선수 연봉변화 등의 여러가지 선형적 데이터의 변화 규칙을 찾아 예측할 수 있게 된다.

3. 추천시스템에 사용되는 특이분해의 원리

• 추천시스템에서 두개의 행렬로 나눌때 특이분해의 축소형 모델이 사용됨
• 
• 왼쪽특이벡터행렬, 특잇값 행렬, 오른쪽특이벡터행렬

4. 그레디언트벡터, 자코비안행렬, 헤시안행렬

그레디언트벡터

• 벡터를 출력하는 함수를 스칼라 입력변수로 행렬미분해서 얻은 벡터
• 기울기(1차 도함수)로 이루어진 벡터
• 벡터의 길이는 입력변수의 수와 같다.

그레디언트벡터 특징

• contour 플롯(등고선)에 quiver 플롯(화살표)으로 그려서 나타낼 수 있다.
• 즉 그레디언트 벡터는 경사의 급한 정도와 경사가 급한 방향을 가리키는 화살표와 같다.
• 화살표의 길이는 경사의 크기, 길이가 길면 경사가 큼, 길이가 짧으면 경사가 작음
• 화살표의 방향은 단위길이당 함수값의 변화가 큰 방향
• 등고선과 그레디언트 벡터의 방향은 직교한다. : 테일러전개로 증명이 된다.

자코비안행렬

• 벡터를 출력하는 함수를 벡터 입력변수로 행렬미분해서 얻은 행렬
• 벡터함수를 벡터로 미분해서 얻은 행렬의 전치행렬이 자코비안 행렬과 같다.
• 기울기(1차 도함수)로 이루어진 행렬

헤시안행렬

• 2차 도함수로 이루어진 행렬
• 그레디언트벡터를 다시 벡터로 미분해서 얻은 행렬
• 그레디언트벡터의 자코비안행렬의 전치행렬과 같다.
  • 자코비안행렬 : 벡터를 벡터로 미분해서 얻은 행렬
• 구하는 방법
  • 주어진 함수의 그레디언트벡터를 구한다. (벡터를 스칼라로 미분한다)
  • 그레디언트벡터의 자코비안행렬을 구한다. (벡터를 벡터로 미분한다. 전치 한번한다)
  • 구한 행렬을 전치연산한다.
• 함수가 연속이고, 미분가능하다면 헤시안행렬은 대칭행렬이 된다. (정방행렬이다, 고유분해를 할 수 있다, 고유분해의 특징을 따른다)

5. 최적화와 최적제어

최적화 optimization

• 최적화 : 목적함수 f 의 값을 최대 또는 최소가 되도록 하는 독립변수 x 를 찾는 방법
  • 최적화의 대상은 목적함수
  • 목적함수 :
    • 성능함수 performance function (모수의 변화에 함수의 성능을 측정함, 클 수록 좋음)
    • 손실함수 loss function (모수의 변화에 따라 달라지는 출력값의 오차를 측정, 작을 수록 좋음), 비용함수, 오차함수라고도 함
• 최적화를 위한 필요조건 : 최적의 독립변수 x*을 입력했을 때 함수의 도함수 값이 0이 되어야한다.
  • 1차 도함수의 값이 0 인 지점이 최대 또는 최소값 지점이다.
  • 2차 도함수의 값이 - 이면 최대값, + 이면 최소값이다. (간단한 그래프로 확인가능 3차함수-2차함수-1차함수)

최적제어 optimal control

• 최적제어 : 범함수 F 의 값을 최대 또는 최소가 되도록 하는 독립함수 y(x) 를 찾는 방법

• 최적제어의 필요조건 : 최적의 함수 y*(x) 을 입력했을 때 범함수의 도함수 값이 0이 되어야 한다.

• 딥러닝의 GAN 모형 : 현실 데이터와 닮은 데이터를 재현하는데 사용하는 방법으로 다음 범함수의 값을 최대화하는 확률분포함수 p(x) 를 구해준다.

• 

• 이 범함수의 도함수

• 위의 식에서 로그미분과 결합법칙을 사용하여 정리하면

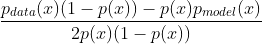
• 이 도함수의 값을 0으로 만드는 최적 확률분포함수 p(x) 는

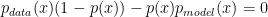
• 수식을 정리하면,

6. 확률변수의 확률분포함수를 설명하는 대표값

• 현실 데이터와 확률변수의 관계에서 발생하는 기술통계값의 의미
  • $\text{E}[X], \text{E}[\bar{X}], \text{Var}[X], \text{Var}[\bar{X}], S^{2}, \text{E}[S^2]$
• 확률분포함수의 모양을 설명하는 기댓값과 분산을 계산하기 위한 과정의 의미

확률변수의 확률분포의 의미

• 1. 현실의 데이터는 모두 확률변수에서 생성된 데이터 집합이다.
  • 데이터셋에서 각각의 독립변수는 각각의 확률변수로 부터 생성
• 2. 확률변수의 확률분포함수를 알면 데이터 분석의 필요한 값들을 계산할 수 있다.
  • 확률분포함수는 확률질량함수(pmf), 누적분포함수(cdf), 확률밀도함수(pdf) 등이 있다.
  • 데이터셋은 불완전하므로 확률변수를 통해서 정확한 값들을 알아 낼 수 있다.
• 3. 하지만 확률변수를 알기 위해서 데이터셋으로부터 역설계하여 유추해야 한다.
• 4. 확률변수의 확률분포함수를 알기 위해서는 분포의 모양을 표현하는 대표값들이 필요하다.
  • 기댓값(평균) : 분포의 위치
  • 분산 : 분포의 폭, 신뢰도
• 5. 대표값들을 계산하여 확률분포를 알게 되면 데이터셋의 특징을 수치화할 수 있게된다.
• 6. 데이터셋으로부터 확률변수를 유추하는 과정에서 여러가지 오차들이 발생하게 된다.
  • 이 오차들을 보완하는 과정에서 선형대수의 기술통계값들에 대해서 이해할 수 있게 된다.

확률분포의 기댓값

• 1. $\text{E}[X]$ : 기댓값은 범함수이다. 범함수는 함수를 입력받는 함수이다.
  • 실수를 입력받는 함수는 일반적인 함수이다.
• 2. 확률분포의 모양을 설명하는 대표값으로 기댓값은 확률분포의 위치를 나타낸다.
  • 즉 확률분포가 어떤 구간(지점)에서 확률이 높은지를 알 수 있으므로 기댓값은 가장 확률이 높은 구간(지점)을 의미한다.
• 3. 그런데 확률변수 X의 기댓값은 구하기 어렵다. 따라서 표본평균을 구하여 기댓값을 알 수 있다.
  • 확률변수를 데이터셋으로부터 유추해야 하므로 알지 못한다.
  • 표본평균 즉 데이터셋의 평균도 표본평균확률변수로 부터 나왔다고 할 수 있다.
• 4. 표본평균 확률변수 $\bar{X}$는 확률변수 X의 복사본인 X1-Xn의 확률변수의 평균을 모아놓은 것과 같다.
  • 표본평균 확률변수의 기댓값은 원래 확률변수의 기댓값과 같다.
  • $\text{E}[\bar{x}] = \text{E}[X]$
• 5. 즉 데이터셋의 표본평균은 표본평균 확률변수에서 나온 것이고 이 값의 기댓값이 원래 확률변수 X의 기댓값과 같다.
• 6. 표본평균 확률변수의 분산을 구하여 신뢰도를 알 수 있다.
  • 얼마나 정확한 값인지 신뢰도를 분산을 통해 알 수 있다.
• 7. 표본평균 확률변수의 분산은 원래 확률변수의 분산보다 1/N 만큼 작다.
  • 분산이 작다는 것은 신뢰도가 높다는 것을 의미한다.
  • 어떤 분포의 분산이 작을 수록 한 곳으로 몰리기 때문
  • $\text{Var}[\bar{X}] = \dfrac{1}{N} \text{Var}[X]$
• 8. 데이터의 갯수(N)가 무한대로 커질 수록 표본평균 확률변수의 분산은 0에 가까워지고 기댓값은 결정론적 값이 된다.
  • 표본평균 확률변수의 값이 고정된다는 의미
• 9. 따라서 데이터셋의 평균을 표본평균 확률변수의 기댓값과 같고, 표본평균 $\bar{x}$는 확률변수 X의 기댓값과 거의 같아진다.
  • 데이터가 무한하게 많지 않으므로 표본평균은 기댓값의 근처에서 나오게 된다.

확률분포의 분산

• 1. 데이터셋은 불완전하므로 분포가 한쪽으로 쏠리게 된다.
• 2. 따라서 표본평균이 편향된 데이터 쪽으로 치우치게 된다.
  • 편향의 정도가 크진 않고 확률변수의 기댓값 근처이다.
• 3. 표본평균이 편향되면 그 만큼 표본분산이 작아진다.
  • 표본분산은 데이터와 평균의 거리이므로 이 거리가 작아진다.
  • 표본평균과 마찬가지로 표본분산도 편향된다.
• 4. 이론적인 분산인 $\sigma^2 = \text{Var}[X]$은 기댓값이 정확하므로 이 값과 같은 비편향 표본분산을 구한다.
  • $\sigma^2 = \text{E}[(X-\mu)^2]$
• 5. 비편향 표본분산은 표본분산의 기댓값으로부터 구할 수 있다.
  • $\text{E}[S^2] = \dfrac{N-1}{N} \sigma^2$
  • 이론적인 분산보다 작아지게 된다.
• 6. 이 식으로부터 비편향 표본분산이 유도 된다.
  • $\sigma^2 = \dfrac{N}{N-1} \text{E}[S^2]$
• 7. 즉 이론적 분산과 같은 표본분산은 비편향 표본분산이고 표본분산을 N/N-1 만큼 확대한 값과 같다.
  • 데이터가 10개이면 10/9 즉 1.1배 표본분산을 확대해야 이론적 분산과 같아진다는 의미이다.

7. 모수추정 방법

• 모수추정 방법
  • 모멘트 방법 : 이론적 모멘트값과 표본의 모멘트값이 같다고 가정
  • 최대가능도 추정 방법 : 가능도 함수값을 최대로 만드는 변수 모수값을 추정하는 방법
  • 베이즈 추정 방법 :

7-1. 모수추정의 의미

• 데이터 분석의 기본은 현실 데이터가 어떤 확률변수로부터 재현된(샘플링 된) 표본의 집합이라고 가정
• 이러한 확률변수의 확률분포를 알면 이 확률분포에서 나올 수 있는 데이터는 모두 일관된 기술통계값을 갖는다.
  • 즉 이 확률분포에서 반복하여 데이터를 샘플링해도 항상 같다.
• 확률변수의 확률분포를 아는 것은 확률분포의 특징을 아는 것과 같다.
  • 확률분포의 모멘트 : 기댓값, 분산, 비대칭도, 첨도
  • 이러한 특징을 알 수 있으면 어떤 확률분포인지 알 수 있고, 어떤 확률변수에서 표본 데이터가 만들어지는지 알 수 있기때문이다.
• 확률분포는 이 모멘트들을 모수로 표현할 수 있으므로, 모수들을 알면 확률분포를 정의 할 수 있다.
• 그러나 현실 데이터만으로 확률분포의 모멘트(모수)를 아는 것은 어렵다.
• 따라서 모수를 추정해야하는데 모수 추정을 위한 3가지 방법이 사용된다.
  • 1. 모멘트 방법
  • 2. 최대가능도 방법
  • 3. 베이즈 추정 방법
• 이러한 방법들로 확률분포의 모수를 추정할 수 있으며 추정에 대해 어느정도 신뢰할 수 있는지 판단과정을 거쳐 확률분포를 정의할 수 있다.
• 예를들어 어떤 예측문제를 풀기위한 예측모형을 만들고, 이로부터 반환 된 N개의 예측값들이 있다면, 이 값들도 확률변수의 표본으로 보고 이 확률변수의 확률분포를 안다면 많은 예측값들 중에서 가장 신뢰도가 높은 값을 선택할 수 있게 되는 것이다.

7-2. 확률분포의 추정

• 기본적으로 현실 데이터의 분포 특성을 통해서 어느정도 확률분포를 유추할 수 있다.
  • 데이터의 유형, 데이터의 분포도, 데이터의 특징들을 통해서 확률분포를 유추할 수 있다.
  • 정확하게 맞는 것은 아니지만 대략적으로 이런 확률분포를 따를 것이라는 것을 알 수 있다.
• 데이터의 히스토그램에 따른 확률분포 추정
  • 데이터가 0또는 1인 경우 : 베르누이 분포
  • 데이터가 카테고리 값인 경우 : 카테고리 분포
  • 데이터가 0과 1사이의 실수값인 경우 : 베타분포
  • 데이터가 0 또는 양수인 경우 : 로그정규분포, 감마분포, F분포, 카이제곱분포, 지수분포, 하프코시분포 등등
  • 데이터의 크기 제한이 없는 경우 : 정규분포, 스튜던트t분포, 코시분포, 라플라스 분포 등등
  • 데이터의 상황에 따라서 달라질 수 있다.

데이터의 종류 확인

• 실수형, 이진, 카테고리
• df["x1"].describe()
  • min, max, mean, std 값 확인 하여 실수형인지 카테고리인지 판단가능
• df["x1"].unique()
  • 카테고리 데이터인 경우 어떤 데이터들이 있는지 판단가능
• count, term = sp.histogram(df["x1"], bins=100)
  • 독립변수를 bins 구간으로 나누고 구간별 데이터의 갯수를 반환해준다.
  • count : 구간별 데이터의 갯수
  • term : bins로 나눈 구간
  • term[np.argmax(count)] : 데이터가 많은 갯수의 인덱스를 사용하여 구간을 인덱싱한다. 즉 가장 데이터가 많은 구간을 반환한다.

데이터의 분포 확인

• 실수형 데이터 :
  • sns.distplot(df["x1"], bins=100, kde=False, rug=False, norm_hist=False, fit=sp.stats.norm)
    • bins : 나누는 구간의 갯수
    • kde : 확률분포 그래프
    • rug : 구간별 데이터의 갯수 표시
    • norm_hist : True 이면 확률밀도함수의 값이 y축에 표시된다. False이면 갯수.
    • fit : 독립변수의 모수추정을 통한 확률분포 그래프를 그려준다.
  • 분포의 종류 : scipy api에서 distribution 검색
    • 베르누이분포 : sp.stats.bernoulli
    • 이항분포 : sp.stats.binom
    • 베타분포 : sp.stats.beta
    • 베타프라임분포 : sp.stats.betaprime
    • 코시분포 : sp.stats.cauchy
    • 하프코시분포 : sp.stats.halfcauchy
    • 카이제곱분포 : sp.stats.chi2
    • 카이분포 : sp.stats.chi
    • 지수분포 : sp.stats.expon
    • 감마분포 : sp.stats.gamma
    • 라플라스분포 : sp.stats.laplace
    • 정규분포 : sp.stats.norm
    • F분포(Fratio) : sp.stats.f
    • 스튜던트t분포 : sp.stats.t
  • df["x1"].hist(bins)
    • 구간별 데이터의 갯수를 나타내준다.
• 카테고리형 데이터 : sns.countplot()

7-3. 모멘트 방법

• 모멘트 방법은 현실 데이터의 모멘트값과 추정하고자 하는 확률변수의 모멘트(이론적 모멘트)값이 같다고 가정하는 방법이다.
  • 데이터 분포가 정규분포인 경우 데이터의 표본평균값과 정규분포의 기댓값이 같다고 보는 것
• 간단하게 확률분포의 모수를 추정할 수 있는 방법이지만, 어느정도 신뢰할 수 있는 값인지 알 수 없다.

7-4. 최대가능도 추정 방법

• 추정된 확률분포로부터 확률밀도함수(또는 확률질량함수)를 구하고, 이를 가능도 함수로 나타낸다.
  • 가능도함수는 확률밀도함수의 상수값과 변수를 바꾼 것을 의미한다.
  • 가능도함수에서는 모수가 변수이고, 입력값(표본값)이 상수항과 같다.
  • 확률밀도함수에서는 반대이다.
• 가능도 함수를 사용하는 것은 현실의 표본값을 입력값으로 하여 모수값을 출력하는 것과 같다.
  • 가능도함수는 확률밀도함수의 변수만 바뀐 것이므로 입력값과 출력값의 관계는 확률밀도함수를 따른다.
• 입력값이 여러개 있는 경우, 각각의 표본은 서로 다른 확률변수에서 나온 것과 같으므로 서로 독립이다.
• 따라서 모수와 상수(입력값)항으로 이루어진 다변수 결합확률밀도함수를 구하는 것과 같다.
  • 확률변수가 독립인 경우 결합확률밀도값은 주변확률밀도값의 곱과 같다.
  • 즉 표본이 N개인 가능도함수는 개별 표본의 주변확률밀도의 곱이다.
• 가능도함수는 각각의 표본에 대한 주변확률밀도값의 곱으로 계산된다.
• 주변확률밀도함수의 곱을 정리하면 어떤 함수의 형태가 된다.
• 이 함수의 최대값을 만드는 모수를 찾기 위해 미분을 한다.
  • 모수로 미분을 하고, 도함수값이 0이 되는 모수의 값을 찾는다.
  • 이 정리과정에서 여러개의 곱의 형태를 쉽게 계산하기 위해서 로그변환을 한다.
  • 로그변환한 가능도함수를 로그가능도함수라고 한다.
  • 이러한 방법을 최대가능도 추정 방법이라고 한다. (MLE : Maximum Likelihood Estimation)
• 즉 최적화에서 목적함수를 찾고 목적함수를 미분하여 최대값 혹은 최소값을 찾는 것과 같은 방식이다.
• 이렇게 추정한 모수값이 우리가 찾고자 하는 확률변수의 확률분포의 모수이고, 이 확률분포를 토대로 데이터 분석(회귀, 분류 등)의 결과값이 된다.

7-5. 베이즈 추정 방법

• 베이즈 추정방법(Bayesian estimation)은 모숫값이 가질 수 있는 모든 가능성이 있는 분포를 계산하는 작업이다.
  • 베이즈 정리를 사용하여 모수의 사후분포를 계산한다.
  • 모수의 사후분포 = 가능도 x 모수의 사전분포
  • 즉 조건부확률을 구하는 것과 같다.
• 모수의 사전분포는 베이지안 추정을 하기전에 알게된 모수 mu의 분포이다. 이 분포를 알지 못하는 경우 균일분포, 베타분포(Beta(1, 1)), 정규분포(N(0,sigma2)) 분포를 사용할 수 있다.
  • 이러한 분포를 무정보분포라고 한다.
• 모수의 사후분포는 N개의 표본이 주어졌을 때의 mu에 대한 조건부 확률분포이다. 베이즈 추정방법으로 구하고자 하는 분포이다.
• 가능도 분포는 mu가 어떤 값으로 주어졌을 때 N개의 표본이 나올 수 있는 확률값과 같다.
• 베이즈 추정법을 사용한 모수 추정 방법
  • 모수적 방법 : 모수의 분포를 다른 확률분포로 나타낸다. 이 확률분포의 모수를 하이퍼파라미터라고 한다. 모수적 방법은 하이퍼파라미터를 계산하는 작업.
  • 비모수적 방법 : 모수의 분포와 동일한 분포인 실제 표본 집합을 만들고 이 집합으로 분포를 표현한다. 몬테카를로 방법이 있다.
• 베이즈 추정방법은 구하고자하는 모수값의 신뢰도를 계산하는 것과 같다.
  • 베이즈 추정방법은 모수를 확률변수로 보기때문에 확률밀도함수를 갖는다.
  • 가능성이 높은 값을 찾는 방법이다.

베이즈 추정 방법의 장점

• 베이즈 추정 방법의 장점은 순차적이라는 점이다.
• 새로운 데이터가 추가된 경우 추가된 데이터에 대해서만 계산하면 된다.
  • 왜냐하면 하이퍼파라미터를 새로운 데이터가 추가 될때마다 누적하여 갱신하기 때문
  • 갱신된 하이퍼파라미터에 대한 pdf만 구하면 된다.
  • 즉 계산량이 증가하지 않는다.
• 최대가능도방법은 새로운 데이터가 추가 되면 기존의 데이터와 합한 전체 데이터에 대한 계산을 새로 해야한다.
  • 즉 데이터가 증가될 때마다 계산량도 늘어난다.

베이즈 추정 방법 계산과정

• 베이즈 정리식에 따라서 각 요소를 정의한다.
  • 가능도함수, 모수의 사전분포
  • 정규화 상수(분모)는 구하지 않아도 된다. 정규화된 값이므로 조건부확률에서는 크게 중요하지 않다.
• 모수의 사전분포 정의
  • $p(\mu)$ 이므로 함수의 변수가 u이다.
  • 예를들어 구하고자 하는 분포가 베르누이분포라면 베이즈 추정에 사용할 사전분포는 베타분포를 사용할 수 있다.
  • 베르누이 분포의 pdf에 베타분포의 모수 a, b를 넣는다.
  • 사전분포의 형태는 구하고자 하는 분포의 형태와 모수값만 다르고 같다.
• 가능도 함수 정의
  • $p(x_1, x_2, \cdots, x_N | \mu)$
  • 표본이 N개인 경우이므로 모든 표본이 독립관계이다. 따라서 가능도는 모든 표본의 주변확률밀도함수의 곱이다.
• 모수의 사후분포 정의
  • 사후분포 = 가능도 x 사전분포
  • $p(\mu | x_1,\cdots,x_N) = p(x_1,\cdots,x_N | \mu) \times p(\mu)$
  • 즉 연속된 곱으로 이루어진 가능도와 같은 pdf인 사전분포가 곱해지면서 지수값에 변화가 생긴다.
  • 이 지수를 정리하면, 사전분포의 모수에 가능도의 지수가 더해진다.
  • 즉 하이퍼파라미터가 갱신된다.
• 이 갱신된 하이퍼파라미터를 사용하여 확률분포를 나타내면 신뢰도가 높은 모수값을 추정할 수 있다.

8. 검정

• 귀무가설, 대립가설 정의하기
• 귀무가설의 모수를 적용한 확률분포 객체 생성하기
• 대립가설에 맞는 유의확률 계산 (t0는 검정통계량값, F(t0)는 누적분포함수)
  • 우측검정 유의확률 : Ha : x > x0 = p(t >= t0 | H0)
    • 연속확률변수 : 1 - F(t0)
  • 이산확률변수 : 1 - F(t0 - 1)
  • 좌측검정 유의확률 : Ha : x < x0 = p(t <= t0 | H0)
    • 연속, 이산확률 변수 : F(t0)
• 유의확률과 유의수준 비교
  • 유의확률 > 유의수준 : 귀무가설 채택, 대립가설 기각
  • 유의확률 < 유의수준 : 귀무가설 기각, 대립가설 채택
  • 유의수준 : 일반적으로 상황에따라서 1%, 5%, 10% 등 사용

검정 과정

• 상품 A의 상품평 총 20개, 좋아요 11개, 싫어요 9개 인 경우 이 상품은 정말 좋은 것인가?
  • 좋아요가 싫어요 보다 많으므로 좋은 상품이라고 할 수 있는가?
  • 좋아요가 나올 확률 11/20으로 이 상품이 좋다고 할 수 있는가?
• 표본이 0과 1인 베르누이 확률분포를 따른다.
  • 베르누이 분포의 모수는 1이 나올 확률이다.
• 검정을 위해서 검정통계량을 구한다.
  • 베르누이분포의 검정통계량은 표본의 합.
  • t0 = 좋아요의 갯수 = 11
• 검정통계량이 따르는 확률분포를 정의한다.
  • 이항분포
• 전체 데이터의 수 : N=20, 귀무가설 : H0 : mu = 0.5
  • 이항분포 객체 생성 : rv = sp.stats.binom(N, mu)
• 대립가설이 이 상품은 "좋다"라면 : Ha : mu > 0.5
• 우측검정 유의확률을 계산한다.
  • 이항분포가 이산확률변수의 표본에 해당하므로 : 1 - F(t0 - 1)
  • 1 - rv.cdf(t0 - 1)
• 유의확률이 41%이면 유의수준보다 크다.
  • 따라서 대립가설이 맞다고 볼 수 없다.
  • 상품 A는 좋다고 할 수 없다. 즉 안좋다.

검정 패키지

• 이항검정 : sp.stats.binom_test(x, n=None, p=0.5, alternative="two_sided")
  • 베르누이 분포의 N번 시행에서 모수값 검정
• 카이제곱 검정 : sp.stats.chisquare(f_obs, f_exp=None)
  • 카테고리 분포의 N번 시행에서 모수값 검정
• 카이제곱 독립검정 : sp.stats.chi2_contingency(f_obs)
  • 두 카테고리 독립변수의 독립, 상관관계 계산
  • 귀무가설은 두 독립변수는 같다이다.
• 단일표본 z검정 : z통계량 함수를 만들고 누적분포함수를 계산한다.
  • 분산 값을 정확하게 아는 정규분포의 모수값에 대한 검정
• 단일표본 t검정 : sp.stats.ttest_1samp(x1, popmean=0)
  • 분산 값을 정확하게 모르는 경우 정규분포의 모수값에 대한 검정
  • 통계량은 자유도가 N-1인 스튜던트t분포를 따른다.
• 독립표본 t검정 : sp.stats.ttest_ind(x1, x2, equal_var=True)
  • 두개의 정규분포에서 나온 N1, N2 개의 데이터 셋에서 기대값이 동일한지 검정
  • 두 분포의 분산값이 같은 경우와 다른 경우에 t통계량이 다름
    • 인수설정이 다름 : 잘 모르면 False
  • N1, N2는 다를 수 있다. N1, N2의 갯수가 작으면 2종오류 발생가능
• 대응표본 t검정 : sp.stats.ttest_rel(x1, x2)
  • 두개의 정규분포에서 나온 N1, N2 개의 데이터 셋에서 기대값이 동일한지 검정
  • 독립표본 t검정에서 두 집단의 표본이 1대1로 대응하는 경우에 대한 검정
  • N의 갯수가 작아도 오류가 발생하지 않는다.
• 등분산검정 :
  • 두 개의 정규분포에서 생성 된 데이터 집합의 분산이 같은지 검정
  • 각각의 검정 방법마다 유의확률이 다르게 나올 수 있다.
  • np.std(x1), np.std(x2)
  • sp.stats.bartlett(x1, x2)
  • sp.stats.fligner(x1, x2)
  • sp.stats.levene(x1, x2)
  • 등분산 검정을 해보고 독립표본 t검정에서 equal_var 인수에 사용할 수 있다.
• 정규성검정 :
  • 확률분포가 가우시안 정규분포를 따르는지 확인하는 검정
    • 독립변수가 가우시안 정규분포를 따른다는 확률론적 선형 회귀모형의 정의에 의해서 가중치값을 추정하고, 회귀계수의 표준오차를 계산하여 추정치의 신뢰구간을 구할 수 있다.
  • 회귀분석에서 중요하다.
  • 여러가지 검정 방법들이 있다.

9. 엔트로피

엔트로피

• 함수를 입력으로 받아 스칼라값을 출력하는 범함수에 해당한다.
  • functional
• 확률분포의 모양을 묘사한다.
• 확률분포가 갖는 정보량을 의미한다.
  • 엔트로피가 크면 정보량은 작아진다.
    • 베르누이 분포에서 0과 1의 확률이 0.5로 같은 경우
  • 엔트로피가 작을 수록 정보량은 커진다.
    • 베르누이 분포에서 0과 1중 한쪽에 확률이 몰려 있는 경우
• 엔트로피의 최대값은 클래스의 갯수에 따라사 달라질 수 있다.
• 엔트로피의 최소값은 0이다.
  • log2p(x)에 의해서 극한값을 사용한다.

python

• sp.stats.entropy(p1, base=2)

지니계수

• 엔트로피 공식과 달리 log2가 사용되지 않으므로 계산이 빠르다.
  • 의사결정나무에서 지니계수가 사용된다.

결합 엔트로피

• joint entropy
• 결합확률분포를 사용한 엔트로피
  • 특정한 값에 확률이 모여 있으면 엔트로피가 0에 가까워지고, 골고루 분포 되어 있으면 1에 가까워진다.

조건부 엔트로피

• conditional entropy
• 확률변수 X가 다른 확률변수 Y의 값을 예측하는데 도움이 되는지를 측정하는 방법
  • X의 값이 고정될때 Y의 값도 고정되면 예측에 도움이 된다.
  • X의 값이 고정될때 Y의 값이 여러개로 분포되어 있으면 예측에 도움이 되지 않는다.
  • 직관적으로 생각해도 이해할 수 있다.
• 이와 같은 조건부엔트로피의 특징을 분류문제에 적용하면 어떤 요소가 클래스에 미치는 영향을 계산할 수 있다.
• 스펨메일 분류문제의 경우 키워드 X1, X2, X3가 있는지 없는지에 따른 스펨, 정상 메일의 엔트로피를 구할 수 있다.
  • 조건부 엔트로피가 작을 수록 어떤 키워드가 스펨 메일이라고 판단하는데 도움을 주는지 구분할 수 있다.
• 붓꽃 분류문제의 경우 어떤 특징 벡터의 기준값에 따라서 클래스와 조건부 엔트로피 값의 변화를 확인 할 수 있다.
• 분류모형인 의사결정나무는 조건부 엔트로피 값을 사용한 모형이다.

교차 엔트로피

• cross entropy
• 교차 엔트로피는 확률분포를 입력으로 받는다.
  • 엔트로피, 결합 엔트로피, 조건부 엔트로피는 확률변수를 입력으로 받는다.
• 교차 엔트로피를 사용하여 분류모형의 성능을 측정할 수 있다.
  • 분류모형의 예측이 나쁠 수록 교차 엔트로피의 값이 커진다.
• p(yk)분포와 q(yk)분포의 차이를 의미한다.
  • p(yk) 분포 : X의 값이 고정 되었을때 갖는 y값의 분포
  • q(yk) 분포 : X의 값이 고정 되었을때 예측값이 갖는 분포

로그손실, 카테고리 로그손실

• log-loss
• 교차 엔트로피의 이러한 특징에 의해 예측의 틀리정도를 나타내는 오차함수로 사용할 수 있다.
  • 교차 엔트로피를 목적함수로 사용하면 최적화를 할 수 있다.
• 이진분류문제서 N개의 학습데이터 전체에 대한 교차엔트로피의 평균은 로그손실이 된다.
• categorical log-loss
• 다중분류문제의 교차엔트로피 손실함수는 카테고리 로그손실이라고 한다.

python

• from sklearn.metrics import log_loss
• log_loss(df["y"], df["y_hat"])

쿨벡-라이블러 발산

• kullback-leibler divergence
• 두 확률분포의 분포모양이 얼마나 다른지를 나타낸다.
  • 교차엔트로피 - 엔트로피 (H[p, q] - H[p])
• 두 분포가 완전히 같으면 log2 부분에서 1이 되어 엔트로피 값이 0이된다.
• 반대로 쿨벡값이 0이면 두 분포는 같다고 할 수 있다.
• 또한 쿨벡은 두 확률분포의 거리가 아니라 차이나는 정도를 나타내므로 확률분포의 위치가 달라지면 값도 달라질 수 있다.

상호정보량

• mutual information
• 쿨벡-라이블러 발산에 해당한다.
• 결합확률밀도함수 p(x, y)와 주변확률밀도함수 p(x), p(y)의 곱의 쿨벡-라이블러 발산이다.
  • MI[X, Y] = KL(p(x,y)||p(x)p(y))
• 상호정보량은 엔트로피와 조건부엔트로피의 차이와 같다.
  • MI[X, Y] = H[X] - H[X|Y]
  • MI[Y, X] = H[Y] - H[Y|X]
• 상호정보량은 두 확률변수의 독립, 상관 여부를 의미한다.
  • 두 확률변수가 독립이면 상호정보량이 0이된다.
  • 두 확률변수가 상관관계이면 상호정보량이 그 만큼의 값을 갖는다.

python

• from sklearn.metrics import mutual_info_score
• [mutual_info_score(X[:, i], y) for i in range(X.shape[0])]

최대정보 상관계수

• maximal information coefficient, MIC
• 연속확률변수에서 상호정보량(상관관계)를 측정하려면 확률변수의 분포를 알아야한다.
• 확률분포는 히스토그램을 사용하여 구간에 대한 값의 분포로 추정할 수 있다.
• 이때 구간의 갯수에 따라서 추정오차가 커질 수 있다.
• 구간을 나누는 방법을 다양하게 시도하여 여러 상호정보량을 계산하고 가장 큰 값을 정규화한 것을 의미한다.
• 특히 비선형 관계의 확률변수들은 피어슨상관계수가 0이지만, 최대정보 상관계수는 상관계수를 측정할 수 있다.

python

• from minepy import MINE
• mine = MINE()
• mine.compute_score(x1, y1)
• mine.mic() : 값 반환