MagnetiCalc

🍀 Always looking for beta testers!

What does MagnetiCalc do?

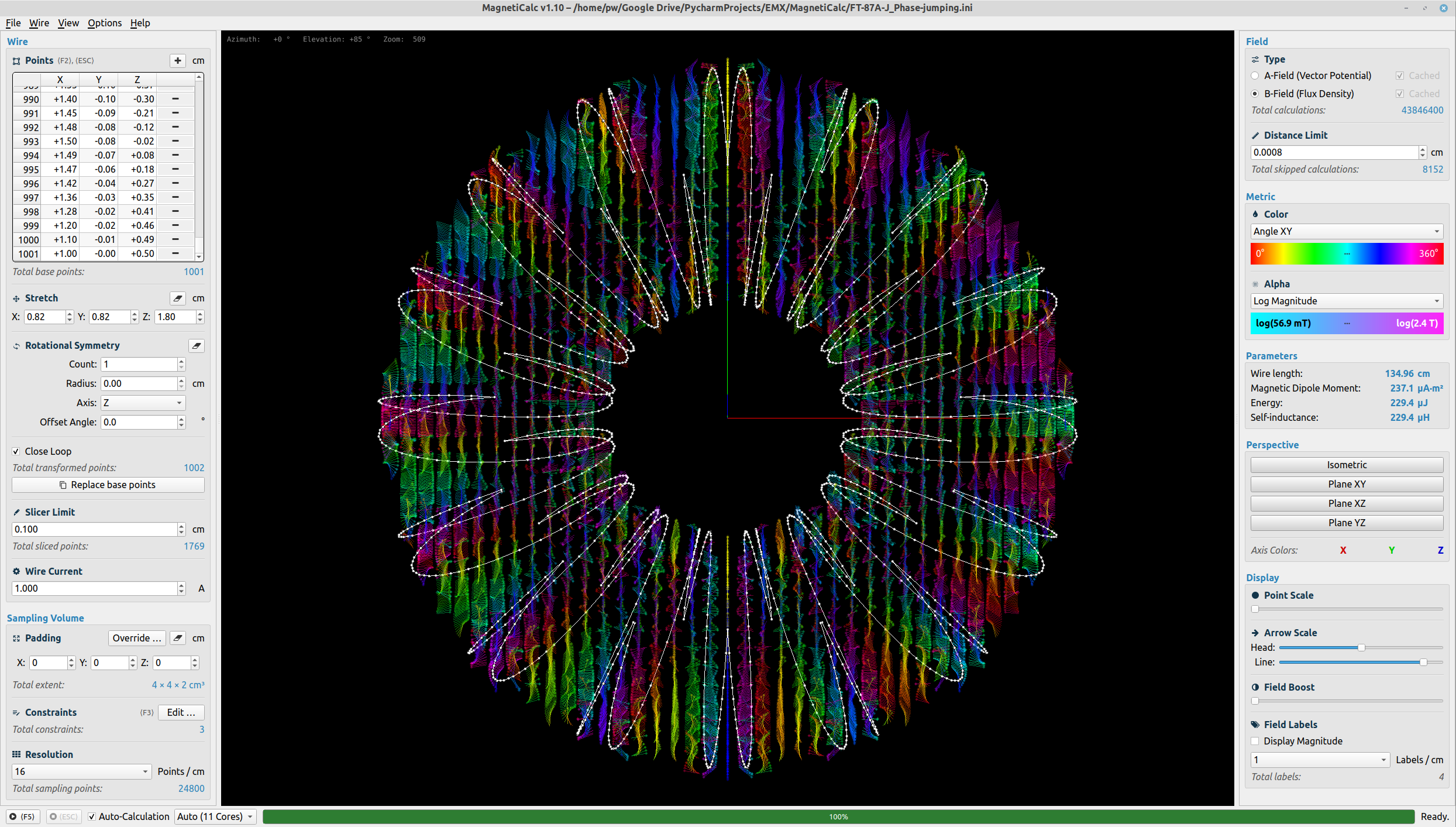
MagnetiCalc calculates the static magnetic flux density, vector potential, energy, self-inductance and magnetic dipole moment of arbitrary coils. Inside an OpenGL-accelerated GUI, the magnetic flux density ($\mathbf{B}$-field, in units of Tesla) or the magnetic vector potential ($\mathbf{A}$-field, in units of Tesla-meter) is displayed in interactive 3D, using multiple metrics for highlighting the field properties.

Experimental feature: To calculate the energy and self-inductance of permeable (i.e. ferrous) materials, different core media can be modeled as regions of variable relative permeability; however, core saturation is currently not modeled, resulting in excessive flux density values.

Who needs MagnetiCalc?

MagnetiCalc does its job for hobbyists, students, engineers and researchers of magnetic phenomena. I designed MagnetiCalc from scratch, because I didn't want to mess around with expensive and/or overly complex simulation software whenever I needed to solve a magnetostatic problem.

How does it work?

The $\mathbf{B}$-field calculation is implemented using the Biot-Savart law [1], employing multiprocessing techniques; MagnetiCalc uses just-in-time compilation (JIT) and, if available, GPU-acceleration (CUDA) to achieve high-performance calculations. Additionally, the use of easily constrainable "sampling volumes" allows for selective calculation over grids of arbitrary shape and arbitrary relative permeabilities $\mu_r(\mathbf{x})$ (experimental).

The shape of any wire is modeled as a 3D piecewise linear curve. Arbitrary loops of wire are sliced into differential current elements ($\mathbf{\ell}$), each of which contributes to the total resulting field ($\mathbf{A}$, $\mathbf{B}$) at some fixed 3D grid point ($\mathbf{x}$), summing over the positions of all current elements ($\mathbf{x^{'}}$):

$\mathbf{A}(\mathbf{x})=I \cdot \frac{\mu_0}{4 \pi} \cdot \displaystyle \sum_\mathbf{x^{'}} \mu_r(\mathbf{x}) \cdot \frac{\mathbf{\ell}(\mathbf{x^{'}})}{\mid \mathbf{x} - \mathbf{x^{'}} \mid}$

$\mathbf{B}(\mathbf{x})=I \cdot \frac{\mu_0}{4 \pi} \cdot \displaystyle \sum_\mathbf{x^{'}} \mu_r(\mathbf{x}) \cdot \frac{\mathbf{\ell}(\mathbf{x^{'}}) \times (\mathbf{x} - \mathbf{x^{'}})}{\mid \mathbf{x} - \mathbf{x^{'}} \mid}$

At each grid point, the field magnitude (or field angle in some plane) is displayed using colored arrows and/or dots; field color and alpha transparency are individually mapped using one of the various available metrics.

The coil's energy $E$ [2] and self-inductance $L$ [3] are calculated by summing the squared $\mathbf{B}$-field over the entire sampling volume; ensure that the sampling volume encloses a large, non-singular portion of the field:

$E=\frac{1}{\mu_0} \cdot \displaystyle \sum_\mathbf{x} \frac{\mathbf{B}(\mathbf{x}) \cdot \mathbf{B}(\mathbf{x})}{\mu_r(\mathbf{x})}$

$L=\frac{1}{I^{2}} \cdot E$

Additionally, the scalar magnetic dipole moment $m$ [4] is calculated by summing over all current elements:

$m=\Bigl| I \cdot \frac{1}{2} \cdot \displaystyle \sum_\mathbf{x^{'}} \mathbf{x^{'}} \times \mathbf{\ell}(\mathbf{x^{'}}) \Bigr|$

References

[1]: Jackson, Klassische Elektrodynamik, 5. Auflage, S. 204, (5.4).
[2]: Kraus, Electromagnetics, 4th Edition, p. 269, 6-9-1.
[3]: Jackson, Klassische Elektrodynamik, 5. Auflage, S. 252, (5.157).
[4]: Jackson, Klassische Elektrodynamik, 5. Auflage, S. 216, (5.54).

Screenshot

(Screenshot taken from the latest GitHub release.)

Examples

Some example projects can be found in the examples/ folder.

If you feel like your project should also be included as an example, you are welcome to file an issue!

Installation

If you have trouble installing MagnetiCalc, make sure to file an issue so I can help you get it up and running!

Requirements:

• Python 3.6+

Tested with:

• Python 3.7 in Linux Mint 19.3
• Python 3.8 in Ubuntu 20.04
• Python 3.8.2 in macOS 11.6 (M1)
• Python 3.8.10 in Windows 10 (21H2)
• Python 3.10.5 in Ubuntu 20.04
• Python 3.12.4 in Ubuntu 24.04

Prerequisites

On some systems, it may be necessary to upgrade pip first: python3 -m pip install pip --upgrade

Note: Windows users need to type python instead of python3

Linux

The following dependencies must be installed first (Ubuntu 20.04):

sudo apt install python3-dev
sudo apt install libxcb-xinerama0 --reinstall

Windows

It is recommended to install Python 3.8.10. Installation will currently fail for Python 3.9+ due to missing dependencies.

On some systems, it may be necessary to install the latest Microsoft Visual C++ Redistributable first.

macOS (M1)

On Apple Silicon, Open Using Rosetta must be enabled for the Terminal app before installing (upgrading) and starting MagnetiCalc.

Option A: Automatic install via pip

This will install (upgrade) MagnetiCalc (and its dependencies) to the user site-packages directory and start it.

Linux & macOS (Intel)

python3 -m pip install magneticalc --upgrade
python3 -m magneticalc

Windows

python -m pip install --upgrade magneticalc
python -m magneticalc

macOS (M1)

Note: On Apple Silicon, JIT may need to be disabled due to incomplete support, resulting in slow calculations.

python3 -m pip install magneticalc --upgrade
export NUMBA_DISABLE_JIT=1 && python3 -m magneticalc

Juptyer Notebook & Jupyter Lab

From within a Jupyter Notebook, MagnetiCalc can be installed (upgraded) and run like this:

import sys
!{sys.executable} -m pip install magneticalc --upgrade
!{sys.executable} -m magneticalc

Option B: Manual download

Note: Windows users need to type python instead of python3.

Install (upgrade) all dependencies to the user site-packages directory:

python3 -m pip install numpy numba scipy PyQt5 vispy qtawesome sty si-prefix h5py --upgrade

Use Git to clone the latest version of MagnetiCalc from GitHub:

git clone https://github.com/shredEngineer/MagnetiCalc

Enter the cloned directory and start MagnetiCalc:

cd MagnetiCalc
python3 -m magneticalc

Enabling CUDA Support

Tested in Ubuntu 20.04, using the NVIDIA CUDA 10.1 driver and NVIDIA GeForce GTX 1650 GPU.

Please refer to the Numba Installation Guide which includes the steps necessary to get CUDA up and running.

License

Copyright © 2020–2022, Paul Wilhelm, M. Sc. <anfrage@paulwilhelm.de>

ISC License

Permission to use, copy, modify, and/or distribute this software for any purpose with or without fee is hereby granted, provided that the above copyright notice and this permission notice appear in all copies.

THE SOFTWARE IS PROVIDED "AS IS" AND THE AUTHOR DISCLAIMS ALL WARRANTIES WITH REGARD TO THIS SOFTWARE INCLUDING ALL IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS. IN NO EVENT SHALL THE AUTHOR BE LIABLE FOR ANY SPECIAL, DIRECT, INDIRECT, OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN ACTION OF CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.

Contribute

You are invited to contribute to MagnetiCalc!

General feedback, Issues and Pull Requests are always welcome.

If this software has been helpful to you in some way or another, please let me and others know!

Documentation

The documentation for MagnetiCalc is auto-generated from docstrings in the Python code.

Debugging

If desired, MagnetiCalc can be quite verbose about everything it is doing in the terminal:

• Some modules are blacklisted in Debug.py, but this can easily be changed.
• Some modules also provide their own debug switches to increase the level of detail.

Data Import/Export and Python API

GUI

MagnetiCalc allows the following data to be imported/exported using the GUI:

• Import/export wire points from/to TXT file.
• Export $\mathbf{A}$-/$\mathbf{B}$-fields, wire points and wire current to an HDF5 container for use in post-processing.
  Note: You could use Panoply to open HDF5 files. (The "official" HDFView software didn't work for me.)

API

The API class (documentation) provides basic functions for importing/exporting data programmatically.

Example: Wire Export

Generate a wire shape using NumPy and export it to a TXT file:

from magneticalc import API
import numpy as np

wire = [
    (np.cos(a), np.sin(a), np.sin(16 * a) / 5)
    for a in np.linspace(0, 2 * np.pi, 200)
]

API.export_wire("Custom Wire.txt", wire)

Example: Field Import

Import an HDF5 file containing an $\mathbf{A}$-field and plot it using Matplotlib:

from magneticalc import API
import matplotlib.pyplot as plt

data = API.import_hdf5("examples/Custom Export.hdf5")
axes = data.get_axes()
a_field = data.get_a_field()

ax = plt.figure(figsize=(5, 5), dpi=150).add_subplot(projection="3d")
ax.quiver(*axes, *a_field, length=1e5, normalize=False, linewidth=.5)
plt.show()

The imported data is wrapped in a MagnetiCalc_Data object (documentation) which provides convenience functions for accessing, transforming and reshaping the data:

Method	Description
.get_wire_list()	Returns a list of all 3D points of the wire.
.get_wire()	Returns the raveled wire points as three arrays.
.get_current()	Returns the wire current.
.get_dimension()	Returns the sampling volume dimension as a 3-tuple.
.get_axes_list()	Returns a list of all 3D points of the sampling volume.
.get_axes()	Returns the raveled sampling volume coordinates as three arrays.
.get_axes(reduce=True)	Returns the axis ticks of the sampling volume.
.get_a_field_list() .get_b_field_list()	Returns a list of all 3D vectors of the $\mathbf{A}$- or $\mathbf{B}$-field.
.get_a_field() .get_b_field()	Returns the raveled $\mathbf{A}$- or $\mathbf{B}$-field coordinates as three arrays.
.get_a_field(as_3d=True) .get_b_field(as_3d=True)	Returns a 3D field for each component of the $\mathbf{A}$- or $\mathbf{B}$-field, indexed over the reduced axes.

ToDo

Functional

• Add a histogram for every metric.
• Add an overlay for vector metrics, like gradient or curvature (derived from the fundamental $\mathbf{A}$- and $\mathbf{B}$-fields).
• Add a list of objects, for wires and permeability groups (constraints), with a transformation pipeline for each object; move the Wire widget to a dedicated dialog window instead. (Add support for multiple wires, study mutual induction.)
• Interactively display superposition of fields with varying currents.
• Add (cross-)stress scalar metric: Ratio of absolute flux density contribution to actual flux density at every point.
• Highlight permeability groups with $\mu_r \neq 0$ in the 3D view.
• Add support for multiple current values and animate the resulting fields.
• Add support for modeling of core material saturation and hysteresis effects.
• Provide a means to emulate permanent magnets.

Usability

• Move variations of each wire preset (e.g. the number of turns) into an individual sub-menu; alternatively, provide a dialog for parametric generation.
• Add stationary coordinate system and ruler in the bottom left corner.
• Add support for selective display over a portion of the metric range, enabling a kind of iso-contour display.
• HDF5 container export from command line, without opening the GUI.

Known Bugs

• Fix issue where the points of a sampling volume with fractional resolution are not always spaced equidistantly for some sampling volume dimensions.
• Fix calculation of divergence right at the sampling volume boundary.
• Fix missing scaling of VisPy markers when zooming.
• Fix unnecessary shading of VisPy markers.

Performance

• Parallelize sampling volume calculation which is currently slow.

Code Quality

• Add unit tests.

Video

A very short demo of MagnetiCalc in action:

Links

There is also a short article about MagnetiCalc on my personal website: paulwilhelm.de/magneticalc

Appendix: Metrics

Metric	Symbol	Description
Magnitude	$\mid\vec{B}\mid$	Magnitude in space
Magnitude X	$\mid\vec{B}_{X}\mid$	Magnitude in X-direction
Magnitude Y	$\mid\vec{B}_{Y}\mid$	Magnitude in Y-direction
Magnitude Z	$\mid\vec{B}_{Z}\mid$	Magnitude in Z-direction
Magnitude XY	$\mid\vec{B}_{XY}\mid$	Magnitude in XY-plane
Magnitude XZ	$\mid\vec{B}_{XZ}\mid$	Magnitude in XZ-plane
Magnitude YZ	$\mid\vec{B}_{YZ}\mid$	Magnitude in YZ-plane
Divergence	$\nabla\cdot\vec{B}$	Divergence
Divergence +	$+{\nabla\cdot\vec{B}}_{>0}$	Positive Divergence
Divergence –	$-{\nabla\cdot\vec{B}}_{<0}$	Negative Divergence
Log Magnitude	$\log_{10} \mid\vec{B}\mid$	Logarithmic Magnitude in space
Log Magnitude X	$\log_{10} \mid\vec{B_X}\mid$	Logarithmic Magnitude in X-direction
Log Magnitude Y	$\log_{10} \mid\vec{B_Y}\mid$	Logarithmic Magnitude in Y-direction
Log Magnitude Z	$\log_{10} \mid\vec{B_Z}\mid$	Logarithmic Magnitude in Z-direction
Log Magnitude XY	$\log_{10} \mid\vec{B}_{XY}\mid$	Logarithmic Magnitude in XY-plane
Log Magnitude XZ	$\log_{10} \mid\vec{B}_{XZ}\mid$	Logarithmic Magnitude in XZ-plane
Log Magnitude YZ	$\log_{10} \mid\vec{B}_{YZ}\mid$	Logarithmic Magnitude in YZ-plane
Log Divergence	$\log_{10} \ \ \nabla\cdot\vec{B}$	Logarithmic Divergence
Log Divergence +	$\log_{10} \ +{\nabla\cdot\vec{B}}_{>0}$	Positive Logarithmic Divergence
Log Divergence –	$\log_{10} \ -{\nabla\cdot\vec{B}}_{<0}$	Negative Logarithmic Divergence
Angle XY	$\measuredangle\vec{B}_{XY}$	Field angle in XY-plane
Angle XZ	$\measuredangle\vec{B}_{XZ}$	Field angle in XZ-plane
Angle YZ	$\measuredangle\vec{B}_{YZ}$	Field angle in YZ-plane