scikit-learn-birch.md

# 用scikit-learn学习BIRCH聚类

---

在[BIRCH聚类算法原理](/ml/cluster/birch.md)中，我们对BIRCH聚类算法的原理做了总结，本文就对scikit-learn中BIRCH算法的使用做一个总结。

# 1. scikit-learn之BIRCH类

在scikit-learn中，BIRCH类实现了原理篇里讲到的基于特征树CF Tree的聚类。因此要使用BIRCH来聚类，关键是对CF Tree结构参数的处理。

在CF Tree中，几个关键的参数为内部节点的最大CF数B， 叶子节点的最大CF数L， 叶节点每个CF的最大样本半径阈值T。这三个参数定了，CF Tree的结构也基本确定了，最后的聚类效果也基本确定。可以说BIRCH的调参就是调试B,L和T。

至于类别数K，此时反而是可选的，不输入K，则BIRCH会对CF Tree里各叶子节点CF中样本的情况自己决定类别数K值，如果输入K值，则BIRCH会CF Tree里各叶子节点CF进行合并，直到类别数为K。

# 2. BIRCH类参数

在scikit-learn中，BIRCH类的重要参数不多，下面一并讲解。

1\)**threshold**:即叶节点每个CF的最大样本半径阈值T，它决定了每个CF里所有样本形成的超球体的半径阈值。一般来说threshold越小，则CF Tree的建立阶段的规模会越大，即BIRCH算法第一阶段所花的时间和内存会越多。但是选择多大以达到聚类效果则需要通过调参决定。默认值是0.5.如果样本的方差较大，则一般需要增大这个默认值。

2\)**branching\_factor**：即CF Tree内部节点的最大CF数B，以及叶子节点的最大CF数L。这里scikit-learn对这两个参数进行了统一取值。也就是说，branching\_factor决定了CF Tree里所有节点的最大CF数。默认是50。如果样本量非常大，比如大于10万，则一般需要增大这个默认值。选择多大的branching\_factor以达到聚类效果则需要通过和threshold一起调参决定

3）**n\_clusters**：即类别数K，在BIRCH算法是可选的，如果类别数非常多，我们也没有先验知识，则一般输入None，此时BIRCH算法第4阶段不会运行。但是如果我们有类别的先验知识，则推荐输入这个可选的类别值。默认是3，即最终聚为3类。

4）**compute\_labels**：布尔值，表示是否标示类别输出，默认是True。一般使用默认值挺好，这样可以看到聚类效果。

在评估各个参数组合的聚类效果时，还是推荐使用Calinski-Harabasz Index，Calinski-Harabasz Index在scikit-learn中对应的方法是metrics.calinski\_harabaz\_score.

# 3. BIRCH运用实例

这里我们用一个例子来学习BIRCH算法。

首先，我们载入一些随机数据，并看看数据的分布图：

```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.datasets.samples_generator import make_blobs
# X为样本特征，Y为样本簇类别， 共1000个样本，每个样本2个特征，共4个簇，簇中心在[-1,-1], [0,0],[1,1], [2,2]
X, y = make_blobs(n_samples=1000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.3, 0.4, 0.3], 
                  random_state =9)
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()
```

输出图如下：

![](http://images2015.cnblogs.com/blog/1042406/201612/1042406-20161219214121041-1585077696.png)

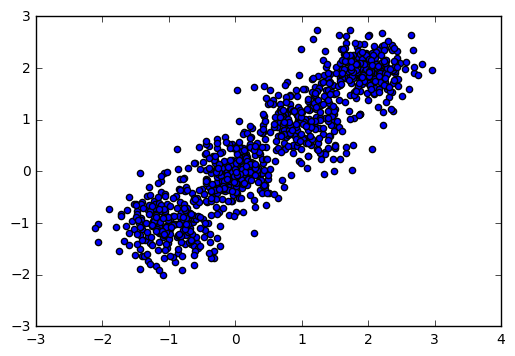
现在我们用BIRCH算法来聚类，首先我们选择不输入可选的类别数K，看看聚类效果和Calinski-Harabasz 分数。

```
from sklearn.cluster import Birch
y_pred = Birch(n_clusters = None).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
from sklearn import metrics
print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
```

输出图如下：

![](http://images2015.cnblogs.com/blog/1042406/201612/1042406-20161219214351932-806165378.png)

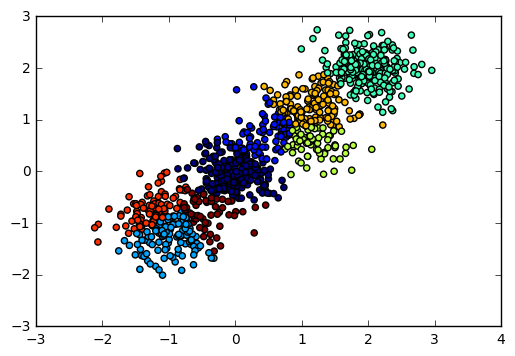
对应的Calinski-Harabasz 分数输出为：

Calinski-Harabasz Score 2220.95253905

由于我们知道数据是4个簇随机产生的，因此我们可以通过输入可选的类别数4来看看BIRCH聚类的输出。代码如下：

```
y_pred = Birch(n_clusters = 4).fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
```

输出图如下：

![](http://images2015.cnblogs.com/blog/1042406/201612/1042406-20161219214625994-33138599.png)

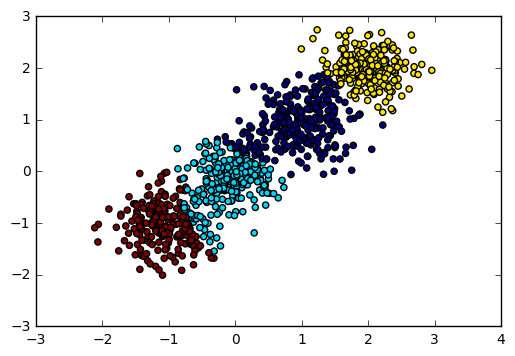
对应的Calinski-Harabasz 分数输出为：

```
Calinski-Harabasz Score 2816.40765268
```

可见如果我们不输入类别数的话，在某些时候BIRCH算法的聚类效果并不一定好，因此这个可选的类别数K一般还是需要调参的。

对于threshold和branching\_factor我们前面还没有去调参，使用了默认的threshold值0.5和默认的branching\_factor值50.

现在我们将threshold从0.5降低为0.3，让BIRCH算法第一阶段的CF Tree规模变大，并观察Calinski-Harabasz 分数。

```
y_pred = Birch(n_clusters = 4, threshold = 0.3).fit_predict(X)
print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
```

对应的Calinski-Harabasz 分数输出为：

Calinski-Harabasz Score 3295.63492273

可见此时的聚类效果有了进一步的提升，那么是不是threshold越小越好呢？我们看看threshold从0.3降低为0.1时的情况。

```
y_pred = Birch(n_clusters = 4, threshold = 0.1).fit_predict(X)
print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
```

对应的Calinski-Harabasz 分数输出为：

```
Calinski-Harabasz Score 2155.10021808
```

也就是说threshold不是越小聚类效果越好。

我们基于threshold为0.3的情况，调试下branching\_factor，将branching\_factor从50降低为20.让BIRCH算法第一阶段的CF Tree规模变大。

```
y_pred = Birch(n_clusters = 4, threshold = 0.3, branching_factor = 20).fit_predict(X)
print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
```

对应的Calinski-Harabasz 分数输出为：

```
Calinski-Harabasz Score 3301.80231064
```

可见调试branching\_factor也可以让聚类分数提高。那么和threshold类似，是不是branching\_factor越小越好呢？我们将branching\_factor从20降低为10，观察聚类分数：

```
y_pred = Birch(n_clusters = 4, threshold = 0.3, branching_factor = 10).fit_predict(X)
print "Calinski-Harabasz Score", metrics.calinski_harabaz_score(X, y_pred)
```

对应的Calinski-Harabasz 分数输出为：

```
Calinski-Harabasz Score 2800.87840962
```

也就是说和threshold类似，branching\_factor不是越小聚类效果越好，需要调参。