This was completed as a quarter long project for the CS 396: Introduction to the Data Science Pipeline course that I took in Summer Quarter 2021. As discussed in the following report, this project consists of a set self-defined of questions to analyze using the data science tools and concepts we covered in the class. All of the source code that was used to generate the results seen in the final report can be seen in the project.ipynb file in this GitHub repository. What follows is the final project report that was written at the end of the quarter as a summary of the full analysis that was made.
With the advent of the internet and its subsequent social media platforms, it has become easier than ever before for businesses to understand their public perception and gather feedback from their customers. Yelp, in particular, has been at the forefront of this movement since its inception. By combining information about the business itself, sourced from the owners and managers, with reviews and tips, sourced from customers, Yelp has become the consensus go-to platform for consumers and businesses alike for measuring public perception. As such, both consumers and business owners have begun to put increasing weight on the sentiments and overall evaluations provided on Yelp, going so far as to even have a measurable weight in business strategy decisions. Due to its growing role in the business world, it is incredibly important to understand any inherent trends or biases that arise within the platform. Yelp, like many other social media platforms, may be subject to behavior or traffic biases that can greatly influence the resulting sentiment on the website. This project aims to study these biases and otherwise trends in order to better understand Yelp as a platform and enable both businesses and consumers to analyze the information it provides more intelligently. In order to accomplish this goal, this project focuses on the four following questions:
- Do more active Yelp users behave differently than infrequent ones?
- Is there a relationship between a reveiw's length and its star rating?
- Do reviews made during business hours have different ratings than those made outside of business hours?
- Do businesses with more reviews have a different star rating distribution compared to those with few?
In order to investigate these proposed questions, I used the following files sourced from the Yelp Open Dataset:
- user.json
- review.json
- review.json, business.json
- business.json
The user.json file contains information about individual users' behavior, such as their number of friends, number of reviews, and average star rating on the reviews they make. By using this data I am able to investigate if there is a correlation between the other features of a user and their average star rating.
The review.json file contains information about individual reviews, such as their star rating, text, and associated business. I used the text and star rating infromation in order to investigate question 2 and used the associated business and star rating in investigating question 3.
The business.json file contains information about individual businesses, such as their star rating, hours, and number of reviews. The information about business hours was used in investigating question 3, while the review count and star rating were used in investigating question 4.
Aside from the data cleaning performed in the next section, I used all of the available data from these datasets in my analysis.
In order to better manage the large Yelp dataset, I transcoded all of the original JSON formatted files to the more efficient pickle format. By performing this initially time consuming process (>20 minutes processing), I was able to greatly decrease future load times to access the data and also moderately increase data density, saving roughly 1 GB of space overall. Doing this made future analysis much easier, as loading in the large datasets now only took a few seconds as opposed to several minutes, thus greatly increasing the speed and efficiency of the data exploration.
After transcoding the data, I then proceeded to clean the data for null values and outliers. Each dataset was cleaned using its own cleaning function, which was called every time the data was loaded in and produced a small report of any cleaning that was done.
For cleaning the user data, any row with a null entry in any column was removed from analysis. Additionally, any user with more than 10,000 reviews was dropped from the dataset, as the EDA indicated these individuals were extreme outliers. Lastly, the cleaning function also checks for any duplicate 'user_id's in the dataset, as the dataset is supposed to be a subset of unique Yelp users without duplicates. In analysis of this dataset, no duplicate IDs were found, so the cleaning function only alerts the user if a duplicate ID is found and does not coalesce the duplicate entries on its own.
For cleaning the business data, any row which had a null entry in the 'stars', 'review_count', 'is_open', or 'hours' columns had their entry removed from the data. In all, this resulted in roughly 17% of entries being removed for lack of an 'hours' field, which is needed for to investigate question 3. Though this cleaning did remove a significant portion of the business data, the remaining data still provided a sufficiently large sample of over 130,000 businesses for analysis.
For cleaning the review data, any row with a null entry in any column was dropped. Additionally, like with the user data, the function also checks for any errant 'business_id' duplicates and alerts the user if any are found. Again, like with the user data, no instances of duplicate IDs were found in this data.
The exploratory data analysis (EDA) was performed in four sections: Business Data, User Data, Review Data, and Combined Data. A breakdown of the EDA performed in each, along with select plots, is shown below.
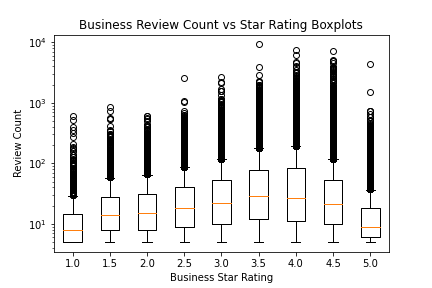
I began the EDA for the business section by plotting histograms of the star rating and review count distributions across businesses. From this, I found that the star rating distribution appears to be heavily left skewed, wtih 5 stars being the most common rating and prevalence decreasing with decreasing rating. I also found that the review count distribution appears to follow a power-law distribution, which is what we would expect given prior knowledge about what situations lead to such a distribution. The most relevant EDA performed in this section was the formation of discrete boxplots for a business' review count vs its star rating. When plotted on a logarithmic scale, as shown below, there is a clear correlation between the star rating and review count. This initial finding appears to indicate that the relationship of interest in question 4 may exist in the data.
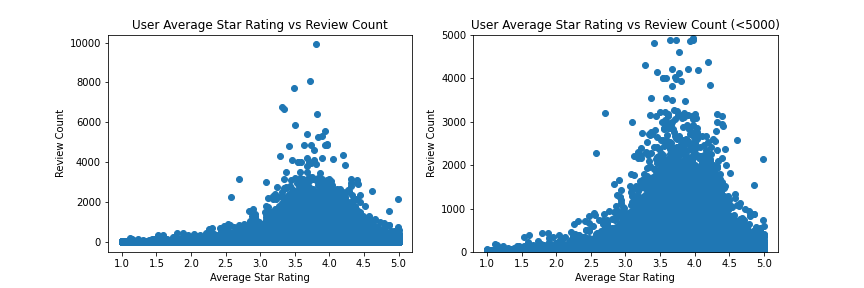
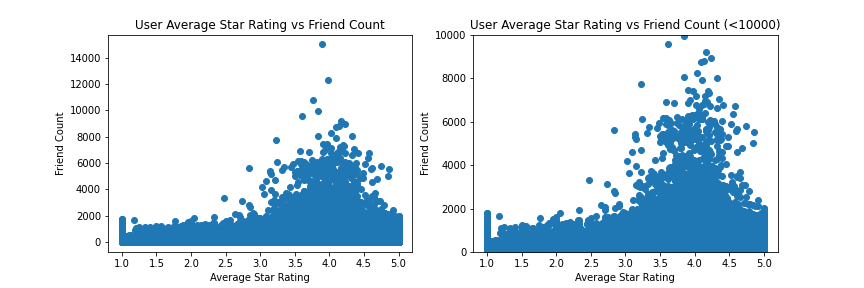
I began the EDA for the business section by analyzing the distribution of user review counts, since this could be used as a measure of activity for question 1. From this, I found that the user review count, much like the business review count, seems to follow a power-law distribution. Next, I analyzed the user friend count distribution, which could also be used as a measure of activity for question 1. In doing this, I found that the distribution was very severly right-skewed, but it does not appear to follow a power-law distribution, as it does not form a linear trend when plotted on a logarithmic scale. Following this, I moved into analyzing the distribution of user average star ratings and plotting it along with other possible factors. In doing this, I found that there seems to be some sort of relationship between average star count and both review count and friend count. This relationship appears to indicate that with increase activity (friends and reviews) a user's average review score gravitates towards around 3.5-4.0 stars.
I also plotted the relationship between user review count and friend count, which seemed to show a faint linear relatinship in logarithmic scale, seeming to indicate that these two features are correlated with another factor, such as time spent on the app or overall activity. The last EDA task performed in this section was the attempts to analyze and model the friend network within the dataset. Upon attempts to compute this network, however, it was shown that this problem was computationally infeasible with the hardware I have available to me.
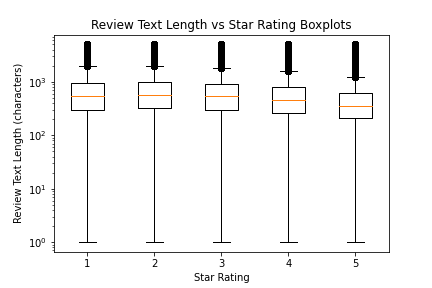
My first step in analzing the review dataset was to plot the distribution of star ratings in the reviews. As anyone familiar with Yelp or online ratings platforms in general may expect, we find this to have a bimodal distribution with peaks at 5 stars and 1 star. This suggests that these reviews are likely made by overly joyous (in the case of 5 star) or overly disdianful (in the case of 1 star) customers with little representation of customers with mixed feelings on the business. My next step in analyzing the review data was to analyze the distribution of reviews by each user and for each business in the dataset. As discussed in this project overview, this analsis led to the conclusion that there would be insufficient data in this dataset to analyze the true distribution of reviews by each user or for each business, as the median number of samples for each was just 1. Following this, I began analyzing the review text length distribution and its relationship to a review's actual rating. In doing this, I created the following boxplots of text length vs star rating. From these we can see that in the logarithmic scale there is a small relationship between text length and star rating.
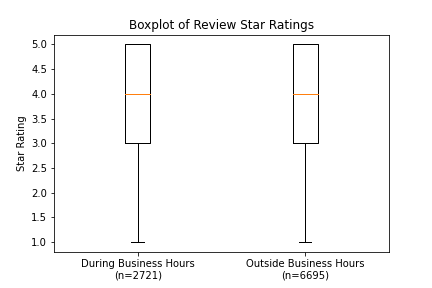
For the combined data section, I analyzed both the business and review dataset in order to answer question 3. In order to do this, I wrote a function that takes in a set of reviews and business data and determines whether the given review occurred during business hours. To decrease the initial computation overhead of doing this analysis, I only performed EDA on a random subset of 10,000 reviews from the full review dataset. From this analysis, I constructed the boxplots shown below. As is clearly seen, there appears to be no correlation between whether a review was written during or outside of business hours and its resulting star rating. One interesting finding from this analysis is that the majority of reviews (typically 60%-75%) come from outside of business hours. My initial thinking was that the majority of reviews would be made during business hours, as people review the business during or shortly after their visit. The data, however, seems to indicate that the opposite is true, and the majority of people write reviews well after their visit to a given business.
The data modeling consisted primarily of graphical representations of the relationships, with some statistical testing and regression analysis performed to verify the graphical observations. The results of this modeling analysis can be seen below categorized by the question it was seeking to investigate.
The first analysis that was performed was to calculate the Pearson and Spearman correlation coefficients for how star rating relates to either a user's friend count or review count. These calculations found that there was a statistically significant correlation in both tests for both relationships. This indicates that there is a relationship between a user's activity and their star rating. However, multiple regression attempts with different combinations and powers of parameters were unable to acheive an R2 greater than 0.1. This is likely the result of the large dispersion of the data, meaning that we are unlikely to be able to generate a predictive model with sufficient accuracy across all users.
In order to further investigate the correlations identified by the Pearson and Spearman, I plotted various features in 3D space color coded by their average star rating. The combination of friend count, review count, and useful votes sent provided the clearest illustration of separation between active and passive users, which can be seen in the plots below as well as in the user_activity_scatter.html and user_activity_medians.html files. In the scatterplot, the overall trend is less obvious, however by grouping the users by their star rating and then taking the median values of these groups, we can see a clear trend in the data. More active users, categorized by high friend count, review count, and useful vote count, tend to have an average review score of between 3.5 and 4.5, a general positive sentiment. In the less active users, we see much more polar star ratings. Infrequent users either leave one or two 5 star reviews and then seemingly never use the platform again, or, more commonly, infrequent users seem to only keep their Yelp accounts active in order to leave negative reviews about bad experiences. This seems to contradict the commonly-held stereotype that frequent Yelp users just "review bomb" business and overall contribute to the negativity on the platform. In fact, what we see here is that it is actually the infrequent users tend to be almost exclusively negative, whereas frequent users of the platform leave high star ratings, though not perfect 5 star ratings.
The first analysis performed on the review text was to calculate the Spearman and Pearson correlation coefficients between a review's text length and its star rating, which showed a statistically significant correlation measure for both coefficients. However, much like with the user features, regression analysis using text length was unable to acheive a high R2, likely because of the large spread of the data in this domain.
Next, I used the Python nltk SentimentIntensityAnalyzer class to obtain the positive, neutral, and negative sentiment scores for the review text. By including the positive and negative sentiment along with the text length in the regression analysis, I was able to generate models with a much higher R2 than was previously possible. In a standard Linear Regression, I consistently obtained R2 values of around 0.40, while using a Gradient Boosting Regressor consistently acheived R2 values above 0.50. Looking at the calculated feature importances for the Gradient Boosting Regressor, we can see that the text length has an exceedingly high feature importants of roughly 0.75, signifying that it is providing a large portion of our predictive power in this regression.
In order to visualize the relationships found during the regression analysis with sentiment included, I plotted reviews in a 3D space based on their postive sentiment, negative sentiment, and text length. These points were then color coded by their star rating in order to visualize their relationship, which can be seen in the plots below and in the sentiment_points.html and sentiment_medians.html files. When grouping these points by their star rating and take the median of these groups, as I did for the prior analysis, I found that there is a clear inverse relationship between text length and star rating. In general, reviews with a lower star rating tend to have a longer overall text length than those with higher star ratings. It seems that when people are dissatisfied with a business and write a negative review, they spend significant time writing out their complaints of the business, whereas positive reviewers tend to have less to comment about other than their overall pleasant experience. Interestingly, the review text length peaks for the 2 star rating group, which may be because reviews with this rating arise when the reviewer had a very bad experience, which they will thus speak at length about in their review, but still had some degree of positive experience, since they chose a 2 star rating over the lower 1 star, meaning they may also have some positive things to say as well. This duality of talking points may lead to a longer review overall, as the reviewer has more topics and sentiments that they wish to cover in their review text.
In analyzing the effect of business hours on review scoring, I had initially planned to perform testing on the samples to identify if they were derived from the same overall distribution. However, this analysis could not be conducted for several reasons. One of these reasons was that the distributions for the star ratings appears to be an inverse normal distribution, meaning I could not rely on using standard testing that utilized characteristics of a normal distribution or central limit theorem convergence to one. Additionally, the data was unable to satisfy the necessary requirements for other distribution tests, such as the Kolmogorov-Smirnov test. While the Kolmogorov-Smirnov 2 sample test would have been very useful, as its results do not rely on characteristics of the underlying distribution, I was unable to use it because the distribution did not meet the requirement of being fully defined. Since the business star ratings are discrete values, the distribution of them is not fully defined and thus means that the results of the Kolmogorov-Smirnov test are not accurate.
With the inability to perform statistical testing on the similarities on the distributions, I instead had to rely on the histograms and boxplots exclusively to determine the similarities between the distributions. As can be seen in the plots below, it is clear that there is no difference in the star rating distributions between reviews made during and outside of business hours. The histograms overlay nearly perfectly, as do the side-by-side boxplots. One interesting finding from this analysis was that only 30% of the reviews in this dataset were made during business hours, which is contrary to what I would have thought initially. Though it is important to note that this value may actually be incorrect, as I discuss later in the limitations of this analysis.
In order to analyze the relationship between a business' review count and its star rating, I first computed the Spearman and Pearson correlation coefficients between the log of the review count and the number of stars. I used the log for the review count for this analysis because, as identified in the EDA, the review count appears to follow a power law distribution. Thus by transforming it to a logarithmic scale I will be able to better model the relationship between it and the business' star rating. Like with the previous correlation coefficients, both coefficients were calculated to be statistically signficant, indicating that there is a relationship between these features.
Next, in order to model this relationship, I created several linear regressions that aimed to determine the logarithmic review count from the star rating. Through this analysis, it was found that a signficant increase in R2 occured between the standard linear model and a 2-degree polynomial model of stars. This R2 value further increased with the model of log(review_count) = a0 + a1*stars + a2*stars2 + a3*stars3. Though this R2 value is still relatively small (<0.10), this is again likely due to the large spread of the data causing a diminishment of the R2 value.
In order to better visualize the relationship between business review count and star rating, I created two 3D plots shown below and in the business_scatter.html and business_histograms.html plots. The first plot, shown on the left, is a 3D density plot with business review count and star rating on the horizontal axes, and the number of businesses in each category on the vertical axis. The second plot shown on the right represents the same information as the first, but now uses individual histograms for each of the star ratings to represent the overall distribution. In this we can see that the distributions for polar star ratings (5 and 1) are much narrower and concentrated at low review counts, whereas intermediate star ratings (3-4) have a much wider range of review counts, with the center being at a higher review count than the polar star ratings. When plotting the previously found regression on the horizontal plane, we can clearly see this observed trend where businesses with polar star ratings tend to have much fewer reviews than those with more neutral star ratings. This seems to indicate that, like with the user data, the business star rating tends to converge to between the 3.5-4.5 star range with extended activity.
In all, the investigation of my initial questions led to the following findings for each:
- Low activity users tend to have very polar review scores, either a few 5 star reviews or, more commonly, several low 1-2 star reviews, whereas high activity users tend to be relativey positive overall, with median star rating in the 3.5-4.5 range. This suggests that the users "review bombing" businesses are actually infrequent users that only maintain their Yelp accounts to complain about a bad experience, whereas frequent users provide overall positive feedback with a healthy amount of constructive criticism.
- Reviews with a lower star rating tend to have a longer text length, possibly due to the desire to vent about a poor experience at a business. The review text length peaks with 2 star reviews, likely because these reviews contain signficant discussion of negative experiences with the inclusion of some positive ones that merited the selection of a 2 star rating over the minimum 1 star.
- Whether a review was made during or outside of business hours appears to have no effect on the final star rating.
- Busissess with an overall polar star rating (1 or 5 stars) tend to have much lower total reviews than those with more modest overall star ratings. It appears that as a business acquires more user activity and input, their star rating converges to the central range of 3.5-4.5 stars.
The main implication from this analysis is that both users and businesses are now better equipped to understand the data that Yelp provides.
From the user's perspective, they should not rely soley on the star rating of the business in order to determine its merit, but also the cummulative number of reviews on it. A business that has a 5 star rating with only a few dozen reviews may not actually be better than one with a 4 star rating and several hundred reviews. It is likely that the 5 star business just has an inadequate sampling of reviews, and thus its review score is not truly representative of its experience. Similarly for negative sentiment, a business with a 1 star review after only a few reviews may not actually be as bad as it seems on initial glance, as the reviews available may only be from a small subset of infrequent users that bias towards negative sentiment.
From the business' perspective, they should put much more weight on reviews that come from high activity users regardless of their actual star rating. In general, these high activity users trend towards positive sentiment, so if they have chosen to leave a negative review it is likely a truly deserving one worthy of analysis. A review from an infrequent user, be it good or bad, should have less weight given to its rating, as these infrequent users tend to only use their accounts to leave reviews of polar sentiment, and thus may not truly be representative of the sentiment of the full customer base. Additionally, businesses do not have to segregate their review analysis based on whether the review was made during business hours or not, as this analysis has shown that the theory of impulsive review sentiment during business hours does not appear to have any numerical basis in the data.
There are also several improvements that could be made to this analysis in further investigation.
The largest point of further improvemnt is with regards to the Yelp data itself. In order for this analysis to be truly representative of Yelp as whole, the data that is analyzed needs to be a true random sample over the full population of Yelp's data. The data provided in this dataset, however, is clearly not a true random sample, as it is heavily concentrated in just a few states. By obtaining a true random sample of all of Yelp's data, the findings from this analysis would be much more credible and applicable. Additionally, there is potential error in the reported review time for the reviews in the dataset. Though Yelp claims that the review time is accurate to when the review is made, several other sources have quested the validity of this claim. They question that the review time may actually be innacurate, possibly as the result of inaccurate time-zone correction relative to the business or that the posted review time is actually the time when the review is fully processed by Yelp's servers, rather than when it was made by the user themselves. This may have contributed to my finding that the vast majority of reviews are made outside of business hours, and thus may have invalidated this portion of the analysis. For the purpose of the findings here, I take Yelp's claims of review time accuracy to be true, but it is important to note that this may not actually be the case.
An additional source of potential improvement could come from increasing processing power to generate more nuanced models. Because of the scale of the datasets and my limited computing resources, it was computationally infeasible for me to train many models that could have had high predictive power, such as through gradient boosting or a random forest. Further analysis with more processing power or the ability to train models continually over an extended period could lead to much more nuanced and precise numerical models than could be developed in this analysis.