Skip to content

Latest commit

 

History

History
 
 

Heap_Sort

README.md

Heap Sort

Heap Sort is a comparison-based sorting technique performed on a Heap data structure (almost complete binary tree).

EXAMPLE

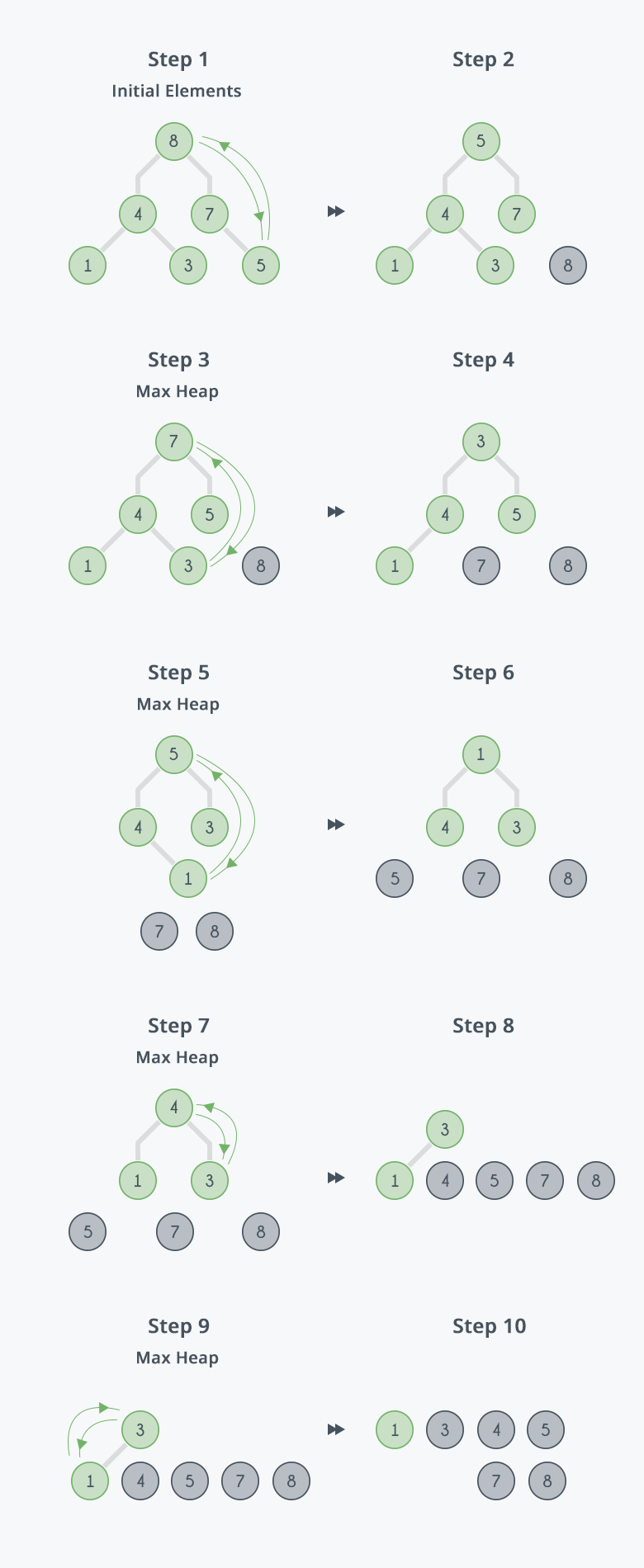
Suppose we have an unsorted array of elements as given below, and it is to be sorted in an ascending order.

Step 1

  • Create a Heap (Min heap for Descending order, Max heap for ascending order)
  • Creation of Heap can be done either by Up Adjustment or by Down Adjustment

Heap Sort

After creation of heap, the array will have elements in the following order :

Heap Sort

Step 2

  • This involves deleting single element from the heap (element at the root) and replacing it with the element at leaf node
  • The deleted element will be stored at the last position in the Sorted Array
  • Since the property of the Heap is now violated, perform Down Adjustment on the root to find correct postion of the element at the root in the new Heap
  • Repeat this step until all elements have been added to the sorted array

Heap Sort

The final Sorted Array looks like this -

Heap Sort

Courtesy: HackerEarth

PSEUDOCODE

Input - Unordered array arr with n elements
Output - Sorted Array
Max Heap is created out of the array arr and then Heap Sort is applied to it 
swap(a,b) swaps the values of a and b

heapSort(arr, n) {
     parent ← n ÷ 2 - 1,
     last ← n - 1
           
     //creation of heap from array arr
     while parent ≥ 0
         downadjustment(arr, parent, n)
         parent ← parent - 1

     //Heap Sort
     while last > 0
         swap(arr[last], arr[0])
         downadjustment(arr, 0, last)
         last ← last - 1
 }
 
 downadjustment(arr, parent, n) {
     
       //until it reaches the leaf node
       while parent * 2 + 1 < n {
       
         //find greatest child and swap with parent
         firstchild ← parent * 2 + 1
         
         if arr[firstchild] < arr[firstchild + 1]
             firstchild ← firstchild + 1
         if arr[parent] < arr[firstchild]
             swap(arr[parent], arr[firstchild])
             parent ← firstchild
         else
             return
     }
 }

COMPLEXITY

Time complexity - О(nlogn), where n is the number of elements in an array.

Space complexity - О(1), since heap is built and sorted in place.

See Also