算法性质
- 基于伯克利Sysadmin decal的linux笔记 + 基于伯克利ds100和cs231n的numpy笔记
@@ -442,12 +442,12 @@
- shell脚本
-Shell 脚本通常以 shebang 行开头:#!path/to/interpreter。
-#!是一个人类可读的 幻数表示 0x23 0x21它可以告诉 shell 将文件其余部分的执行传递给 指定翻译。 如果您的脚本作为可执行文件运行(例如 ./awesome_shell_script) 加上 shebang 行,那么 shell 将调用 可执行文件(通常是解释器)位于 path/to/interpreter运行你的 脚本。 如果您的脚本作为参数传递给解释器,例如 bash awesome_shell_script,那么 shebang 没有效果并且 bash会处理 脚本的执行。
+
Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组
@@ -478,7 +478,7 @@ shell脚本
-
+
@@ -496,7 +496,7 @@ shell脚本
- 基于伯克利ds100和cs231n的numpy笔记
+ 基于伯克利Sysadmin decal的linux笔记
@@ -557,12 +557,12 @@
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组
+
shell脚本
+Shell 脚本通常以 shebang 行开头:#!path/to/interpreter。
+#!是一个人类可读的 幻数表示 0x23 0x21它可以告诉 shell 将文件其余部分的执行传递给 指定翻译。 如果您的脚本作为可执行文件运行(例如 ./awesome_shell_script) 加上 shebang 行,那么 shell 将调用 可执行文件(通常是解释器)位于 path/to/interpreter运行你的 脚本。 如果您的脚本作为参数传递给解释器,例如 bash awesome_shell_script,那么 shebang 没有效果并且 bash会处理 脚本的执行。
@@ -936,7 +936,7 @@
-
+
@@ -954,7 +954,7 @@
- 游戏简评
+ 基于苏大ppt的计算机硬件笔记
@@ -1015,11 +1015,16 @@
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
+
`冯·诺依曼计算机特点
+– 计算机由五大部件组成
+• 输入数据和程序的“输入设备”
+• 记忆程序和数据的“存储器”
+• 完成数据加工处理的“运算器”
+• 控制程序执行的“控制器”
+• 输出处理结果的“输出设备”
@@ -1050,7 +1055,7 @@ 428被封锁的涩谷
-
+
@@ -1068,7 +1073,7 @@ 428被封锁的涩谷
- 爱丽丝的回忆
+ 游戏简评
@@ -1125,10 +1134,11 @@
- 心爱的少女,她诞生的时日是?
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
@@ -1159,7 +1169,7 @@
-
+
@@ -1177,7 +1187,7 @@
- 基于苏大ppt的计算机硬件笔记
+ 爱丽丝的回忆
@@ -1238,16 +1244,10 @@
- `冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
+ 心爱的少女,她诞生的时日是?
diff --git a/page/3/index.html b/page/3/index.html
index 468f5fda7..459c042c9 100644
--- a/page/3/index.html
+++ b/page/3/index.html
@@ -1140,7 +1140,7 @@ 函数
-
+
@@ -1158,7 +1158,7 @@ 函数
- blacksouls人物解析
+ blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
@@ -299,8 +299,8 @@ black souls
diff --git "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html" "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
index 81a37695e..69c513e0d 100644
--- "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
+++ "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
@@ -399,8 +399,8 @@ 游戏杂谈
@@ -419,8 +419,8 @@ 游戏杂谈
@@ -439,8 +439,8 @@ 游戏杂谈
shell脚本
-Shell 脚本通常以 shebang 行开头:#!path/to/interpreter。
-#!是一个人类可读的 幻数表示 0x23 0x21它可以告诉 shell 将文件其余部分的执行传递给 指定翻译。 如果您的脚本作为可执行文件运行(例如 ./awesome_shell_script) 加上 shebang 行,那么 shell 将调用 可执行文件(通常是解释器)位于 path/to/interpreter运行你的 脚本。 如果您的脚本作为参数传递给解释器,例如 bash awesome_shell_script,那么 shebang 没有效果并且 bash会处理 脚本的执行。
+
Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组
@@ -478,7 +478,7 @@shell脚本
shell脚本
- 基于伯克利ds100和cs231n的numpy笔记 + 基于伯克利Sysadmin decal的linux笔记
@@ -557,12 +557,12 @@
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组
+
shell脚本
+Shell 脚本通常以 shebang 行开头:#!path/to/interpreter。
+#!是一个人类可读的 幻数表示 0x23 0x21它可以告诉 shell 将文件其余部分的执行传递给 指定翻译。 如果您的脚本作为可执行文件运行(例如 ./awesome_shell_script) 加上 shebang 行,那么 shell 将调用 可执行文件(通常是解释器)位于 path/to/interpreter运行你的 脚本。 如果您的脚本作为参数传递给解释器,例如 bash awesome_shell_script,那么 shebang 没有效果并且 bash会处理 脚本的执行。
@@ -936,7 +936,7 @@
-
+
@@ -954,7 +954,7 @@
- 游戏简评
+ 基于苏大ppt的计算机硬件笔记
@@ -1015,11 +1015,16 @@
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
+
`冯·诺依曼计算机特点
+– 计算机由五大部件组成
+• 输入数据和程序的“输入设备”
+• 记忆程序和数据的“存储器”
+• 完成数据加工处理的“运算器”
+• 控制程序执行的“控制器”
+• 输出处理结果的“输出设备”
@@ -1050,7 +1055,7 @@ 428被封锁的涩谷
-
+
@@ -1068,7 +1073,7 @@ 428被封锁的涩谷
- 爱丽丝的回忆
+ 游戏简评
@@ -1125,10 +1134,11 @@
- 心爱的少女,她诞生的时日是?
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
@@ -1159,7 +1169,7 @@
-
+
@@ -1177,7 +1187,7 @@
- 基于苏大ppt的计算机硬件笔记
+ 爱丽丝的回忆
@@ -1238,16 +1244,10 @@
- `冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
+ 心爱的少女,她诞生的时日是?
diff --git a/page/3/index.html b/page/3/index.html
index 468f5fda7..459c042c9 100644
--- a/page/3/index.html
+++ b/page/3/index.html
@@ -1140,7 +1140,7 @@ 函数
-
+
@@ -1158,7 +1158,7 @@ 函数
- blacksouls人物解析
+ blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
@@ -299,8 +299,8 @@ black souls
diff --git "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html" "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
index 81a37695e..69c513e0d 100644
--- "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
+++ "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
@@ -399,8 +399,8 @@ 游戏杂谈
@@ -419,8 +419,8 @@ 游戏杂谈
@@ -439,8 +439,8 @@ 游戏杂谈
Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 +
shell脚本
+Shell 脚本通常以 shebang 行开头:#!path/to/interpreter。
+#!是一个人类可读的 幻数表示 0x23 0x21它可以告诉 shell 将文件其余部分的执行传递给 指定翻译。 如果您的脚本作为可执行文件运行(例如 ./awesome_shell_script) 加上 shebang 行,那么 shell 将调用 可执行文件(通常是解释器)位于 path/to/interpreter运行你的 脚本。 如果您的脚本作为参数传递给解释器,例如 bash awesome_shell_script,那么 shebang 没有效果并且 bash会处理 脚本的执行。
-
+
@@ -954,7 +954,7 @@
- 游戏简评
+ 基于苏大ppt的计算机硬件笔记
@@ -1015,11 +1015,16 @@
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
+
`冯·诺依曼计算机特点
+– 计算机由五大部件组成
+• 输入数据和程序的“输入设备”
+• 记忆程序和数据的“存储器”
+• 完成数据加工处理的“运算器”
+• 控制程序执行的“控制器”
+• 输出处理结果的“输出设备”
@@ -1050,7 +1055,7 @@ 428被封锁的涩谷
-
+
@@ -1068,7 +1073,7 @@ 428被封锁的涩谷
- 爱丽丝的回忆
+ 游戏简评
@@ -1125,10 +1134,11 @@
- 心爱的少女,她诞生的时日是?
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
@@ -1159,7 +1169,7 @@
-
+
@@ -1177,7 +1187,7 @@
- 基于苏大ppt的计算机硬件笔记
+ 爱丽丝的回忆
@@ -1238,16 +1244,10 @@
- `冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
+ 心爱的少女,她诞生的时日是?
diff --git a/page/3/index.html b/page/3/index.html
index 468f5fda7..459c042c9 100644
--- a/page/3/index.html
+++ b/page/3/index.html
@@ -1140,7 +1140,7 @@ 函数
-
+
@@ -1158,7 +1158,7 @@ 函数
- blacksouls人物解析
+ blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
@@ -299,8 +299,8 @@ black souls
diff --git "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html" "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
index 81a37695e..69c513e0d 100644
--- "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
+++ "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
@@ -399,8 +399,8 @@ 游戏杂谈
@@ -419,8 +419,8 @@ 游戏杂谈
- 游戏简评 + 基于苏大ppt的计算机硬件笔记
@@ -1015,11 +1015,16 @@
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
+
`冯·诺依曼计算机特点
+– 计算机由五大部件组成
+• 输入数据和程序的“输入设备”
+• 记忆程序和数据的“存储器”
+• 完成数据加工处理的“运算器”
+• 控制程序执行的“控制器”
+• 输出处理结果的“输出设备”
@@ -1050,7 +1055,7 @@ 428被封锁的涩谷
-
+
@@ -1068,7 +1073,7 @@ 428被封锁的涩谷
- 爱丽丝的回忆
+ 游戏简评
@@ -1125,10 +1134,11 @@
- 心爱的少女,她诞生的时日是?
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
@@ -1159,7 +1169,7 @@
-
+
@@ -1177,7 +1187,7 @@
- 基于苏大ppt的计算机硬件笔记
+ 爱丽丝的回忆
@@ -1238,16 +1244,10 @@
- `冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
+ 心爱的少女,她诞生的时日是?
diff --git a/page/3/index.html b/page/3/index.html
index 468f5fda7..459c042c9 100644
--- a/page/3/index.html
+++ b/page/3/index.html
@@ -1140,7 +1140,7 @@ 函数
-
+
@@ -1158,7 +1158,7 @@ 函数
- blacksouls人物解析
+ blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
@@ -299,8 +299,8 @@ black souls
diff --git "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html" "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
index 81a37695e..69c513e0d 100644
--- "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
+++ "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
@@ -399,8 +399,8 @@ 游戏杂谈
@@ -419,8 +419,8 @@ 游戏杂谈
428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 +
`冯·诺依曼计算机特点
+– 计算机由五大部件组成
+• 输入数据和程序的“输入设备”
+• 记忆程序和数据的“存储器”
+• 完成数据加工处理的“运算器”
+• 控制程序执行的“控制器”
+• 输出处理结果的“输出设备”
428被封锁的涩谷
428被封锁的涩谷
- 爱丽丝的回忆 + 游戏简评
@@ -1125,10 +1134,11 @@
- 心爱的少女,她诞生的时日是?
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
@@ -1159,7 +1169,7 @@
-
+
@@ -1177,7 +1187,7 @@
- 基于苏大ppt的计算机硬件笔记
+ 爱丽丝的回忆
@@ -1238,16 +1244,10 @@
- `冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
+ 心爱的少女,她诞生的时日是?
diff --git a/page/3/index.html b/page/3/index.html
index 468f5fda7..459c042c9 100644
--- a/page/3/index.html
+++ b/page/3/index.html
@@ -1140,7 +1140,7 @@ 函数
-
+
@@ -1158,7 +1158,7 @@ 函数
- blacksouls人物解析
+ blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
@@ -299,8 +299,8 @@ black souls
diff --git "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html" "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
index 81a37695e..69c513e0d 100644
--- "a/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
+++ "b/tags/\346\270\270\346\210\217\346\235\202\350\260\210/index.html"
@@ -399,8 +399,8 @@ 游戏杂谈
428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。
@@ -1159,7 +1169,7 @@
-
+
@@ -1177,7 +1187,7 @@
- 基于苏大ppt的计算机硬件笔记
+ 爱丽丝的回忆
@@ -1238,16 +1244,10 @@
- `冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
+ 心爱的少女,她诞生的时日是?
diff --git a/page/3/index.html b/page/3/index.html
index 468f5fda7..459c042c9 100644
--- a/page/3/index.html
+++ b/page/3/index.html
@@ -1140,7 +1140,7 @@ 函数
-
+
@@ -1158,7 +1158,7 @@ 函数
- blacksouls人物解析
+ blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
@@ -299,8 +299,8 @@ black souls
- 基于苏大ppt的计算机硬件笔记 + 爱丽丝的回忆
@@ -1238,16 +1244,10 @@
- `冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
+ 心爱的少女,她诞生的时日是?
diff --git a/page/3/index.html b/page/3/index.html
index 468f5fda7..459c042c9 100644
--- a/page/3/index.html
+++ b/page/3/index.html
@@ -1140,7 +1140,7 @@ 函数
-
+
@@ -1158,7 +1158,7 @@ 函数
- blacksouls人物解析
+ blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
@@ -299,8 +299,8 @@ black souls
`冯·诺依曼计算机特点
-– 计算机由五大部件组成
-• 输入数据和程序的“输入设备”
-• 记忆程序和数据的“存储器”
-• 完成数据加工处理的“运算器”
-• 控制程序执行的“控制器”
-• 输出处理结果的“输出设备”
函数
函数
- blacksouls人物解析 + blacksouls剧情解析
@@ -1219,12 +1219,11 @@
- 尸龙贾巴沃克
-1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
@@ -1255,7 +1254,7 @@ 尸龙贾巴沃克
-
+
@@ -1273,7 +1272,7 @@ 尸龙贾巴沃克
- blacksouls剧情解析
+ blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
@@ -279,8 +279,8 @@ black souls
尸龙贾巴沃克
-1 | 在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!! |
象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
+
冬之钟
+由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
尸龙贾巴沃克
尸龙贾巴沃克
- blacksouls剧情解析 + blacksouls原著梗解析
@@ -1334,11 +1333,11 @@
- 冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html
index 6c464719b..0f8e8dedb 100644
--- a/page/4/index.html
+++ b/page/4/index.html
@@ -239,7 +239,7 @@ thinklive
-
+
@@ -257,7 +257,7 @@ thinklive
- blacksouls原著梗解析
+ blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
+]]>
+
+ 秘密
+
+
+ 秘密
+
+
迪瑞克拉世界观设定集
/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
@@ -7446,24 +7446,6 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
数据结构与算法
-
- blacksouls人物解析
- /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
- 尸龙贾巴沃克
-在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
-象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
-玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
-]]>
-
- 游戏杂谈
- black souls
-
-
- 游戏杂谈
- black souls
-
-
blacksouls剧情解析
/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
@@ -7506,6 +7488,24 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]>
+
+ 游戏杂谈
+ black souls
+
+
+ 游戏杂谈
+ black souls
+
+
+
+ blacksouls人物解析
+ /2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ 尸龙贾巴沃克
+在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
+玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
]]>
游戏杂谈
diff --git a/sitemap.txt b/sitemap.txt
index f1d5d5aeb..16c5181da 100644
--- a/sitemap.txt
+++ b/sitemap.txt
@@ -9,14 +9,14 @@ https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89rpg%
https://thinklive1.github.io/2023/10/14/%E8%8B%8F%E5%A4%A7linux_ppt/
https://thinklive1.github.io/2023/10/14/mit6.006%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/17/thinklive%E7%9A%84%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E5%9B%BE%E4%B9%A6%E9%A6%86/
-https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/09/numpy/
+https://thinklive1.github.io/2023/10/12/sysadmin/
https://thinklive1.github.io/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%9D%80%E6%89%8B47/
https://thinklive1.github.io/2023/09/30/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
-https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E4%B8%96%E7%95%8C%E8%A7%82/
https://thinklive1.github.io/2023/09/29/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89%E8%BD%B6%E4%BA%8B%E9%9B%86/
https://thinklive1.github.io/2023/09/30/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
@@ -26,9 +26,9 @@ https://thinklive1.github.io/2023/10/05/%E5%BB%BA%E7%AB%99%E6%8C%87%E5%8C%97/
https://thinklive1.github.io/2023/09/30/%E5%BD%B1%E5%AD%90%E5%B7%A5%E5%8E%82/
https://thinklive1.github.io/2023/09/29/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/61a%E6%80%BB%E5%92%8C/
-https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
https://thinklive1.github.io/2023/10/05/cpp%20primer%20plus%E6%80%BB%E5%92%8C/
https://thinklive1.github.io/2023/09/29/cs106b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/2023/09/29/cs106l%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -57,8 +57,8 @@ https://thinklive1.github.io/tags/%E5%8C%97%E4%BA%AC%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/linux/
https://thinklive1.github.io/tags/%E7%BC%96%E7%A8%8B%E5%B7%A5%E5%85%B7/
https://thinklive1.github.io/tags/%E7%B3%BB%E7%BB%9F%E7%AE%A1%E7%90%86/
-https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/not-for-broadcast/
+https://thinklive1.github.io/tags/vim/
https://thinklive1.github.io/tags/%E5%B7%AB%E5%B8%88%E4%BA%8C/
https://thinklive1.github.io/tags/hexo/
https://thinklive1.github.io/tags/next/
@@ -69,11 +69,11 @@ https://thinklive1.github.io/tags/%E8%8B%8F%E5%B7%9E%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E6%93%8D%E4%BD%9C%E7%B3%BB%E7%BB%9F/
https://thinklive1.github.io/tags/hitman/
https://thinklive1.github.io/tags/%E6%AD%A5%E8%A1%8C%E6%A8%A1%E6%8B%9F%E5%99%A8/
+https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
https://thinklive1.github.io/tags/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
https://thinklive1.github.io/tags/%E9%BE%99%E8%85%BE%E4%B8%96%E7%BA%AA/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/
@@ -87,8 +87,8 @@ https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E7
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/wrpg/
https://thinklive1.github.io/categories/%E5%BB%BA%E7%AB%99%E7%BB%8F%E9%AA%8C/
https://thinklive1.github.io/categories/%E6%B8%B8%E6%88%8F%E6%9D%82%E8%B0%88/%E5%85%B6%E4%BB%96%E6%B8%B8%E6%88%8F/
+https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
-https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
https://thinklive1.github.io/categories/%E8%BF%AA%E7%91%9E%E5%85%8B%E6%8B%89/
diff --git a/sitemap.xml b/sitemap.xml
index 8a2566d2d..6f7e023ea 100644
--- a/sitemap.xml
+++ b/sitemap.xml
@@ -101,7 +101,7 @@
- https://thinklive1.github.io/2023/10/12/sysadmin/
+ https://thinklive1.github.io/2023/10/09/numpy/
2023-11-27
@@ -110,7 +110,7 @@
- https://thinklive1.github.io/2023/10/09/numpy/
+ https://thinklive1.github.io/2023/10/12/sysadmin/
2023-11-27
@@ -146,7 +146,7 @@
- https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
2023-11-27
@@ -155,7 +155,7 @@
- https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
+ https://thinklive1.github.io/2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
2023-11-27
@@ -164,7 +164,7 @@
- https://thinklive1.github.io/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/2023/09/28/%E7%A7%98%E5%AF%861/
2023-11-27
@@ -254,7 +254,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -263,7 +263,7 @@
- https://thinklive1.github.io/2023/09/29/black%20souls%E5%89%A7%E6%83%85%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -272,7 +272,7 @@
- https://thinklive1.github.io/2023/09/29/blacksouls%E5%8E%9F%E8%91%97%E6%A2%97%E8%A7%A3%E6%9E%90/
+ https://thinklive1.github.io/2023/09/29/black%20souls%E4%BA%BA%E7%89%A9%E8%A7%A3%E6%9E%90/
2023-11-27
@@ -499,14 +499,14 @@
- https://thinklive1.github.io/tags/vim/
+ https://thinklive1.github.io/tags/not-for-broadcast/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/not-for-broadcast/
+ https://thinklive1.github.io/tags/vim/
2023-12-05
weekly
0.2
@@ -583,35 +583,35 @@
- https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
+ https://thinklive1.github.io/tags/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E5%9B%BD%E7%A7%91%E5%AD%A6%E6%8A%80%E6%9C%AF%E5%A4%A7%E5%AD%A6/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/tags/%E4%B8%AD%E7%A7%91%E5%A4%A7/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BB%84%E6%88%90/
+ https://thinklive1.github.io/tags/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
@@ -711,28 +711,28 @@
- https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
+ https://thinklive1.github.io/categories/%E7%A7%98%E5%AF%86/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
+ https://thinklive1.github.io/categories/%E8%80%83%E7%A0%94%E7%AC%94%E8%AE%B0/
2023-12-05
weekly
0.2
- https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%BB%84/
+ https://thinklive1.github.io/categories/%E8%AF%BE%E7%A8%8B%E7%AC%94%E8%AE%B0/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%BD%91%E7%BB%9C/
2023-12-05
weekly
0.2
diff --git a/tags/black-souls/index.html b/tags/black-souls/index.html
index 9df78162f..f052f6e10 100644
--- a/tags/black-souls/index.html
+++ b/tags/black-souls/index.html
@@ -259,8 +259,8 @@ black souls
冬之钟
-由于black souls的故事远远没有完结,因此现阶段我们很难对红白女王与梅贝尔这些与格林牵扯极深的支配者们进行什么定论,只能就已有的剧情和文本进行一些归纳,本期视频我将就bs2比较难懂的一处地方,冬之钟的主线事件,进行一些个人向的分析。
+
01
+众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
diff --git a/page/4/index.html b/page/4/index.html index 6c464719b..0f8e8dedb 100644 --- a/page/4/index.html +++ b/page/4/index.html @@ -239,7 +239,7 @@thinklive
thinklive
- blacksouls原著梗解析 + blacksouls人物解析
@@ -318,11 +318,12 @@
- 01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。
+
尸龙贾巴沃克
+1
在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!!
+象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
diff --git a/search.xml b/search.xml
index 86cffb24f..92e2bbef7 100644
--- a/search.xml
+++ b/search.xml
@@ -4350,6 +4350,70 @@ x(i,j) =
麻省理工
+
+ 基于伯克利ds100和cs231n的numpy笔记
+ /2023/10/09/numpy/
+ Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
+数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
+官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
+>>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
+数组属性
+
+- dtype
+
+>>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
+数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
+切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
+可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
+整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
+可以用整数数组索引修改数组部分值
+import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
+数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
+import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
+转置矩阵, 只需使用 T数组对象的属性:
+import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
+广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
+Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
+import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
+线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
+一起广播两个数组遵循以下规则:
+
+- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
+- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
+- 如果数组在所有维度上都兼容,则可以一起广播。
+- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
+- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
+
+一些应用
+import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
+]]>
+
+ 课程笔记
+ 数据科学
+
+
+ 伯克利
+ 课程笔记
+ python
+ 数据科学
+ pandas
+
+
基于伯克利Sysadmin decal的linux笔记
/2023/10/12/sysadmin/
@@ -4949,70 +5013,6 @@ x(i,j) =
系统管理
-
- 基于伯克利ds100和cs231n的numpy笔记
- /2023/10/09/numpy/
- Numpy 是 Python 中科学计算的核心库。 它提供了高性能的多维数组对象以及使用这些对象的工具 数组。
-数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
-官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]])
array([[ 1., 2.],
[ 3., 4.]])
>>>np.array([x for x in range(5)])
array([0, 1, 2, 3, 4])
>>>np.array([["A", "matrix"], ["of", "words."]])
array([['A', 'matrix'],
['of', 'words.']],
dtype='<U6')
>>>np.ones([3,2])
array([[ 1., 1.],
[ 1., 1.],
[ 1., 1.]])
>>>np.random.randn(3,2)
array([[ 0.3601399 , 1.31206686],
[-0.95112397, 0.62475726],
[-1.24179768, 1.63392069]])
->>>c = np.full((2,2), 7) # Create a constant array
print(c) # Prints "[[ 7. 7.]
# [ 7. 7.]]"
>>>d = np.eye(2) # Create a 2x2 identity matrix
print(d) # Prints "[[ 1. 0.]
# [ 0. 1.]]"
-数组属性
-
-- dtype
-
->>>np.arange(1,5).dtype
dtype('int64')
>>>np.array(["Hello", "Worlddddd!"]).dtype
dtype('<U10')
/*
What does `<U6` mean?
- `<` Little Endian
- `U` Unicode
- `6` length of longest string
*/
>>> np.array([1,2,3]).astype(float)
array([ 1., 2., 3.])
-数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3)
array([[ 1, 2, 3],
[ 4, 5, 6],
[ 7, 8, 9],
[10, 11, 12]])
>>>A.flatten()
array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12])
-切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Use slicing to pull out the subarray consisting of the first 2 rows
# and columns 1 and 2; b is the following array of shape (2, 2):
# [[2 3]
# [6 7]]
b = a[:2, 1:3]
# A slice of an array is a view into the same data, so modifying it
# will modify the original array.
print(a[0, 1]) # Prints "2"
b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1]
print(a[0, 1]) # Prints "77"
-可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4)
# [[ 1 2 3 4]
# [ 5 6 7 8]
# [ 9 10 11 12]]
a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]])
# Two ways of accessing the data in the middle row of the array.
# Mixing integer indexing with slices yields an array of lower rank,
# while using only slices yields an array of the same rank as the
# original array:
row_r1 = a[1, :] # Rank 1 view of the second row of a
row_r2 = a[1:2, :] # Rank 2 view of the second row of a
print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)"
print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
# We can make the same distinction when accessing columns of an array:
col_r1 = a[:, 1]
col_r2 = a[:, 1:2]
print(col_r1, col_r1.shape) # Prints "[ 2 6 10] (3,)"
print(col_r2, col_r2.shape) # Prints "[[ 2]
# [ 6]
# [10]] (3, 1)"
-整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np
a = np.array([[1,2], [3, 4], [5, 6]])
# An example of integer array indexing.
# The returned array will have shape (3,) and
print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]"
# The above example of integer array indexing is equivalent to this:
print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
# When using integer array indexing, you can reuse the same
# element from the source array:
print(a[[0, 0], [1, 1]]) # Prints "[2 2]"
# Equivalent to the previous integer array indexing example
print(np.array([a[0, 1], a[0, 1]])) # Prints "[2 2]"
-可以用整数数组索引修改数组部分值
-import numpy as np
# Create a new array from which we will select elements
a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
print(a) # prints "array([[ 1, 2, 3],
# [ 4, 5, 6],
# [ 7, 8, 9],
# [10, 11, 12]])"
# Create an array of indices
b = np.array([0, 2, 0, 1])
# Select one element from each row of a using the indices in b
print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]"
# Mutate one element from each row of a using the indices in b
a[np.arange(4), b] += 10
print(a) # prints "array([[11, 2, 3],
# [ 4, 5, 16],
# [17, 8, 9],
# [10, 21, 12]])
-数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
-import numpy as np
x = np.array([[1,2],[3,4]])
print(np.sum(x)) # Compute sum of all elements; prints "10"
print(np.sum(x, axis=0)) # Compute sum of each column; prints "[4 6]"
print(np.sum(x, axis=1)) # Compute sum of each row; prints "[3 7]"
-转置矩阵, 只需使用 T数组对象的属性:
-import numpy as np
x = np.array([[1,2], [3,4]])
print(x) # Prints "[[1 2]
# [3 4]]"
print(x.T) # Prints "[[1 3]
# [2 4]]"
# Note that taking the transpose of a rank 1 array does nothing:
v = np.array([1,2,3])
print(v) # Prints "[1 2 3]"
print(v.T) # Prints "[1 2 3]"
-广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = np.empty_like(x) # Create an empty matrix with the same shape as x
# Add the vector v to each row of the matrix x with an explicit loop
for i in range(4):
y[i, :] = x[i, :] + v
# Now y is the following
# [[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]
print(y)
-Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
-import numpy as np
# We will add the vector v to each row of the matrix x,
# storing the result in the matrix y
x = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]])
v = np.array([1, 0, 1])
y = x + v # Add v to each row of x using broadcasting
print(y) # Prints "[[ 2 2 4]
# [ 5 5 7]
# [ 8 8 10]
# [11 11 13]]"
-线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
-一起广播两个数组遵循以下规则:
-
-- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。
-- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。
-- 如果数组在所有维度上都兼容,则可以一起广播。
-- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。
-- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的
-
-一些应用
-import numpy as np
# Compute outer product of vectors
v = np.array([1,2,3]) # v has shape (3,)
w = np.array([4,5]) # w has shape (2,)
# To compute an outer product, we first reshape v to be a column
# vector of shape (3, 1); we can then broadcast it against w to yield
# an output of shape (3, 2), which is the outer product of v and w:
# [[ 4 5]
# [ 8 10]
# [12 15]]
print(np.reshape(v, (3, 1)) * w)
# Add a vector to each row of a matrix
x = np.array([[1,2,3], [4,5,6]])
# x has shape (2, 3) and v has shape (3,) so they broadcast to (2, 3),
# giving the following matrix:
# [[2 4 6]
# [5 7 9]]
print(x + v)
# Add a vector to each column of a matrix
# x has shape (2, 3) and w has shape (2,).
# If we transpose x then it has shape (3, 2) and can be broadcast
# against w to yield a result of shape (3, 2); transposing this result
# yields the final result of shape (2, 3) which is the matrix x with
# the vector w added to each column. Gives the following matrix:
# [[ 5 6 7]
# [ 9 10 11]]
print((x.T + w).T)
# Another solution is to reshape w to be a column vector of shape (2, 1);
# we can then broadcast it directly against x to produce the same
# output.
print(x + np.reshape(w, (2, 1)))
# Multiply a matrix by a constant:
# x has shape (2, 3). Numpy treats scalars as arrays of shape ();
# these can be broadcast together to shape (2, 3), producing the
# following array:
# [[ 2 4 6]
# [ 8 10 12]]
print(x * 2)
-]]>
-
- 课程笔记
- 数据科学
-
-
- 伯克利
- 课程笔记
- python
- 数据科学
- pandas
-
-
基于伯克利cs61b的java数据结构笔记
/2023/10/06/61b%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -5414,45 +5414,6 @@ x(i,j) =
步行模拟器
-
- 游戏简评
- /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
- 428被封锁的涩谷
-希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>
-
- 游戏杂谈
- 其他游戏
-
-
- 游戏杂谈
-
-
-
- 爱丽丝的回忆
- /2023/09/28/%E7%A7%98%E5%AF%861/
-
-
-
-
-
-
-
-
-
-
-]]>
-
- 秘密
-
-
- 秘密
-
-
基于苏大ppt的计算机硬件笔记
/2023/09/29/%E7%A1%AC%E4%BB%B6%E6%80%BB%E5%92%8C%E7%AC%94%E8%AE%B0/
@@ -6264,6 +6225,45 @@ Inexpensive Disk)由美国加州大学伯克利分校提出。
计算机组成
+
+ 游戏简评
+ /2023/09/30/%E6%B8%B8%E6%88%8F%E7%AE%80%E8%AF%84/
+ 428被封锁的涩谷
+希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>
+
+ 游戏杂谈
+ 其他游戏
+
+
+ 游戏杂谈
+
+
+
+ 爱丽丝的回忆
+ /2023/09/28/%E7%A7%98%E5%AF%861/
+
+
+
+
+
+
+
+
+
+
01
-众所周知,black souls的原型,或者说最重要的灵感来源就是爱丽丝梦游仙境以及它衍生的爱丽丝镜中奇遇,我本人一直对游戏和原著的对应关系感到很好奇,但由于工作量很大,一直没下定决心做这件事,但最近突然想到,如果分期做一些整理会不会就没那么麻烦了呢,于是决定开启这个系列。 +
尸龙贾巴沃克
+1 | 在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!! |
象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析
数组
+numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
+创建数组的方法
+>>>np.array([[1.,2.], [3.,4.]]) |
>>>c = np.full((2,2), 7) # Create a constant array |
数组属性
+-
+
- dtype +
>>>np.arange(1,5).dtype |
数组的类型与其包含的数据类型相对应,可以用.astype改变类型
+数组编辑
+重组和展开
+>>>np.arange(1,13).reshape(4,3) |
切片索引和整数索引
+切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
+# Create the following rank 2 array with shape (3, 4) |
可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
+# Create the following rank 2 array with shape (3, 4) |
整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
+import numpy as np |
可以用整数数组索引修改数组部分值
+import numpy as np |
数组的数学运算
+numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
+Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
import numpy as np |
转置矩阵, 只需使用 T数组对象的属性:
import numpy as np |
广播
+我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
+例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
+import numpy as np |
Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
import numpy as np |
线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
一起广播两个数组遵循以下规则:
+-
+
- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。 +
- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。 +
- 如果数组在所有维度上都兼容,则可以一起广播。 +
- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。 +
- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的 +
一些应用
+import numpy as np |
数组
-numpy 数组是一个值网格,所有值都具有相同的类型,并由非负整数组成的元组索引。 它的维度就是数组的秩 ;它的shape就是每个维度的大小组成的元组 b = np.array([[1,2,3],[4,5,6]]) # Create a rank 2 array
print(b.shape) # Prints "(2, 3)"
print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4"
官方数组创建教程 ds100的numpy教程 cs231n的python numpy教程
-创建数组的方法
->>>np.array([[1.,2.], [3.,4.]]) |
>>>c = np.full((2,2), 7) # Create a constant array |
数组属性
--
-
- dtype -
>>>np.arange(1,5).dtype |
数组的类型与其包含的数据类型相对应,可以用.astype改变类型
-数组编辑
-重组和展开
->>>np.arange(1,13).reshape(4,3) |
切片索引和整数索引
-切片时,第一个参数是行,第二个是列,切片形成的是对原来数组的引用,修改子数组也会影响原数组
-# Create the following rank 2 array with shape (3, 4) |
可以混合整数索引和切片索引,这样做会产生一个比原始数组的秩更低的数组
-# Create the following rank 2 array with shape (3, 4) |
整数数组 索引允许你使用另一个数组的数据构造任意数组 大批。 这是一个例子:
-import numpy as np |
可以用整数数组索引修改数组部分值
-import numpy as np |
数组的数学运算
-numpy 提供的数学函数的完整列表 文档 Numpy 提供了更多用于操作数组的函数; 完整的列表 文档
-Numpy 提供了许多有用的函数来执行计算 数组; 最有用的之一是 sum:
import numpy as np |
转置矩阵, 只需使用 T数组对象的属性:
import numpy as np |
广播
-我们有一个较小的数组和一个 较大的数组,并且我们想多次使用较小的数组来执行某些操作 在更大的阵列上。
-例如,假设我们要向每个添加一个常数向量 矩阵的行。 我们可以这样做:
-import numpy as np |
Numpy 广播允许我们执行此计算,而无需实际执行 创建多个副本 v。 考虑这个版本,使用广播:
import numpy as np |
线路 y = x + v尽管有效 x有形状 (4, 3)和 v有形状 (3,)由于广播; 这条线的工作原理就像 v实际上有形状 (4, 3), 其中每一行都是一个副本 v,并且按元素求和。
一起广播两个数组遵循以下规则:
--
-
- 如果数组没有相同的秩,则在前面添加较低秩数组的形状 1s 直到两个形状具有相同的长度。 -
- 如果两个数组具有相同的维度,则称 兼容 它们在维度上 维度中的大小,或者如果其中一个数组在该维度中的大小为 1。 -
- 如果数组在所有维度上都兼容,则可以一起广播。 -
- 广播后,每个数组的行为就好像它的形状等于元素方向 两个输入数组的形状的最大值。 -
- 在一个数组的大小为 1 而另一个数组的大小大于 1 的任何维度中, 第一个数组的行为就好像它是沿着该维度复制的 -
一些应用
-import numpy as np |
希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
-]]>希腊神话将命运女神履行职能的过程写作织网,这无疑是一种极为贴切的比喻,对网状结构来说,在中心处的轻轻一拨,边缘处就是极大的震动,越是深入核心,就越是复杂,但所有分支无论看上去多么没有规律,最后都会收束到中心网点,我想这就是428的编剧想实现的叙事结构。 这样的结构需要极致的严谨和巨大的工作量,正如正统的本格派推理一样丝丝入扣,同时还要维持各个部分的信息量尽量均布,各个网点处都有关键悬念留待读者,但,他们做到了,7位主角的命运与城市里大大小小配角的命运,就这样纠缠在一起,并收束到了一个巨大的阴谋上,更令人称奇的是,尽管使用了这样的结构,制作组仍然做到了悬念的均布,几乎没有出现信息量失衡的情况。 于是,玩家得以在4月28日的涩谷当一天的命运女神,只要在一个个节点上轻轻拨正些许紊乱的蛛丝,蛛丝就会自然而然地化为网状,事实上没有我说的这么轻松,因为这些命运的线条起初似乎是绕成一团,理清它们的过程也少不了误解和错误。 为了确保这个过程的顺畅,85个bad end大部分都有提示,以每一小时为节点,只有理清一小时内的所有事件,命运才能向前推进,起初似乎是一些不成规律的线,但逐渐就开始交错,纠缠,而作为有着神力的玩家,只需要制造一些偶然,改变一两个小小的决定就能够造成一连串的蝴蝶效应。 对这种操控命运的讨论很容易回到一些宿命论的思潮上来,幸运的是428的编剧在这个方面却有着很积极的态度,于是在结局,命运的线条汇聚在一起,无数偶然交错下,产生的必然却孕育着希望,尽管多少有些日式的大团圆味道,但流露出的价值观确实积极的。 如果说这样精巧的叙事结构有没有问题,那么当然也是有的,叙事必须依靠逻辑的支撑,如此庞大的网状结构,逻辑当然不可能天衣无缝,事实上依然有很多巧合和偶然,为了配合结构的需要,甚至部分主角也免不了当工具人,但你很难对此苛责什么,通过有限的角色实现如此复杂的剧本,不免要让一些角色承担过多的推进剧情的作用,相对来说编剧已经做得很不错了。 此外的问题是大部分日式游戏难免的幼稚气,叙事结构是精巧且充满悬念的,但一些抒情节点,以及一些过度夸张以至于模板化的人物性格,依然为其减色不少。不过我也能理解编剧,毕竟这种精密的结构确实很难填补完全恰如其分的内容 总的来说428在叙事结构方面可以说是当今电子游戏的最高峰水平,尽管它的其他部分可能只是优秀或者不错的程度,依旧是一款剧情类的神作
+]]>在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!! |
象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
玛丽苏
-玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。
随后,爱丽丝遇到了前来将她军的红骑士,但埋伏在旁的白骑士反吃了红骑士,护送爱丽丝成王前的最后一段路,这段几乎没有在游戏里的直接对应,除了冬之钟小剧场he中卡罗尔让三姐妹为他挥手帕用了原台词,并且也有说法是白骑士是作者的投影。 但我个人对此有一些猜测,这段很可能对应整个冬之钟剧场,根据一些主流猜测,这段其实是梅贝尔和古兰合谋困住了追击的奈亚,如果我们认为红方是敌方,那么就对应奈亚,指引爱丽丝成王的红王后对应反水的红女王,红骑士表示前来追击的奈亚,白骑士就可能是白女王方的梅贝尔,那么这段剧情就成了,奈亚前来将住格林,梅贝尔前来解围,护送格林到了成王之路
终于,爱丽丝戴上了王冠,格林成了“王”,在此之后的剧情对应很少,青蛙佣人招待爱丽丝去了晚宴,对应游戏中去往古兰晚宴前向海因里希托付女儿,爱丽丝梦醒后红白王后成了黑白两只小猫,对应红女王的台词,可能会在续作有进一步的阐释
至此,对卡罗尔爱丽丝系列的作品就完全结束了,之后有机会可以说说贾巴沃克和猎蛇鲨记
+]]> +在天之繁星哟!命数已定之众哟!尽管去为爱所煎熬吧,为嫉妒之苦吧!呜呼!感激涕零吧!为这幸灾乐祸暗黑舞台点缀色彩就好!!! |
象征着腐败与神秘的紫黑色,遍布全身的缝合痕迹与绷带,恶魔一样的卷曲角,晦暗如死尸的肤色,以及左眼燃烧着的灵魂之火(致敬黑岩射手可能性微存),尸龙姐姐的人物形象无时无刻不在传达着神秘强大而阴暗的气氛,本视频将对尸龙的整个人物进行解析 尸龙在爱丽丝镜中奇遇的原型是一首小诗,这首诗的大意是勇者手提沃伯尔之剑斩杀邪龙贾巴沃克,游戏中也承袭了这一设定,贾巴沃克一直都以死尸的形象登场 要解析这一角色,我们首先从最直接的行为说起,按游戏的时间线,尸龙姐姐大概做了以下这些事 1把童话(具体哪本未知,根据混沌迷宫的狼外婆信息推测可能是小红帽)给了渴望母爱的玛丽.苏,从而激发了虫虫的创作能力,导致她创造出一代的箱庭。顺便一提,关于尸龙和玛丽苏的关系,游戏里没有直接证据支持姐妹说,混沌迷宫提到黑山羊有两个子嗣,米兰达认为尸龙有黑山羊的气息,且明显尸龙和玛丽苏有一定关系,这些是确定的,但并未明说姐妹,有人从克苏鲁的设定中寻找论据,但本人对克系了解不多在此不评价。 2红偶像约会中电影《三人的茶会》提及茶会时期的三人曾经打倒过贾巴沃奇,不知是否和尸龙有关,此外尸龙也曾被昔日的勇者,如今的猎头兔打倒,自称在之后洗心革面,但相关资料太少,我们不知道是不是她放水或另有隐情 3格林被引导进玛丽苏的箱庭开始一代的故事,此时尸龙(不知道玛丽苏是否知情)已经乱入到一代的不思议之国,为格林一行人提供帮助,通关d结局后找她对话,她会直接把二代给剧透了,不过由于时间线上d结局应该直接接上二代,所以“正史”上可能没有这件事,顺便一提,一代的不思议之国是爱丽丝的箱庭,或者说玛丽苏的仿造品,也没有定论,所以很难推测尸龙是入侵还是本来就在那里 4来到二代时间线,由于不思议之国是奈亚的箱庭,而黑山羊则是奈亚的“配偶”,所以尸龙出现在这倒是理所应当,此时的尸龙以四噩梦之一的身份登场,,但工作内容则是在卡罗尔川上堆雪人,以及在格林面前装出温柔大姐姐的形象,十足的关系户做派。 里路线中,格林和米兰达等人可以先后对战三噩梦,以及杀死其余两个噩梦后现出真身的尸龙,值得一提的是这似乎是她全系列中唯一一次全力出手,并且在此战中死亡,但考虑到支配者的特性,是否死透了依旧存疑 以上就是尸龙在系列中的行动,接下来我将对这些行动的目的与尸龙的性格进行归纳。 尸龙首先是一个安静的观察者,一代中她只是在一棵树下扮尸体,二代则在河边堆雪人,如果格林不找她,在里线之前不会和她有任何交集,然而,隐藏和善表面下的真相是尸龙其实是个性格扭曲唯恐天下不乱的乐子人,是她启发了玛丽苏创造自己的黑童话箱庭,间接引发之后所有的故事,而一开始的目的可能只是以玛丽苏面对求而不得的母爱痛苦挣扎的样子为乐,也是她诅咒了狩猎邪龙的英雄,使兔子一族成为贪食尸体的魔兽,其中被沃波尔斩下头颅可能是她行事风格的分界线,其自述死前曾是无恶不作的邪龙,在复活后变得收敛,但其实依旧不改邪龙本质,只是变得只在关键时刻推波助澜 而将这两种性格统一起来的则是她的创作欲,没错,和玛丽苏一样,尸龙对创作也有自己的执念,在玛丽苏涌现起黑暗的创作力之后,尸龙意识到,玛丽苏那邪恶的灵魂一定程度其实是自己的作品,如果说玛丽苏是支配者中第一个创造故事的人,尸龙就是第一个“创作者”,这激发出她内心最深层的欲望,那就是创作出足够黑暗污秽的灵魂,方法则是让一个灵魂在无尽的痛苦与求而不得中循环。 可以说在这点上尸龙和奈亚有一定的共同点,就是让格林经历无数次的痛苦循环,但二者还是有着分歧,奈亚想要的是格林求而不得的爱,尸龙则想要格林本就污秽的灵魂更加黑暗。 这时我们就可以理解尸龙的行为了,由于里线实际上也处于轮回之中,所以对尸龙来说,告诉格林一些真相只会让他的反抗更加激烈,也会在反抗之后更加绝望,这样才符合她的目的。 而以上依旧是贾巴沃克的表层性格,而她隐藏最深的性格则是扭曲的独占欲,在卡罗尔川的地牢中有个四个雪人,分别是玛丽苏,小红帽,爱丽丝和格林,此外,班达斯奈奇的住处也有着一个写着想将其变为收藏品的雪人(sen0才能看到真相),可见尸龙内心最深的欲望其实是独占欲,培育最污秽的灵魂,随后将其收藏起来,这才是尸龙的愿景,但她为何要隐藏这一欲望呢,在qf尸龙失败的逆监禁剧情里,由于尸龙发现格林的灵魂已经黑暗到想要独占自己,尸龙就会唯一一次直接暴露自己的独占欲来收割这个丰硕的成果,然而,奈亚或者其他支配者绝不会容忍这种行为,所以一旦尸龙试图独占格林就会立刻被排除出世界,这就是尸龙一直压抑着独占欲的原因。 此外,根据dlc3入口处的对话以及数量庞大的雪人,或许可以猜测尸龙曾经一边观察一边玩弄过很多灵魂,但这些灵魂最后都因为经历过多的痛苦和绝望后变得麻木,因此才会对有着无穷成长性的格林视若珍宝 一切温柔的言语都不过是为了将格林引导向更绝望的结局,独占污秽的黑之魂,玩到腻后就扔掉,对贾巴沃克之魂的描述为包藏在虚伪的母性之下的独占欲之影可谓恰如其分。 值得一提的是,独占欲这种感情不止在尸龙一人上出现,大部分支配者都有着这种感情,如白之女王诺登就承认自己多次有独占格林的想法,爱丽丝01也曾吐露自己害怕不可控制地想要独占格林,但她们与尸龙的区别则是,她们能够理解人类的爱,并为了人类的幸福选择放手,与红白女王的对比或许也是尸龙人物形象设计的一个目的 现在可以做一个总结了,尸龙姐姐是一个对格林有着强烈爱意的角色,她的母性是虚伪的,但这种爱意却不是,尽管她扭曲,残酷,自私,虚伪,但是她始终知道自己要做什么并理性地付出行动,即使失败了也不失风度从容自若,相较于虫虫几乎写在脸上的扭曲性格,直截了当的作恶行径,以及一有挫败就大呼小叫的行径,尸龙的感情更加内敛,行事也更加隐秘,但可谓是个很有恶人魅力的反派角色 同时,由于bs的碎片化叙事并且尚未完结,关于尸龙依旧有很多谜团,例如她和玛丽苏以及其他支配者的具体关系,里线中她是不是仍然在演戏,她究竟为何会给玛丽苏童话书,尸龙等三噩梦和三个爱丽丝的关系等等,就期待续作的解答了 大家都来和尸龙姐姐做朋友吧,尸门
玛丽苏
+玛丽苏,作为bs中自称的女主角,是bs唯二个三代都有出场(包括红森)的支配者,还有一个是贾巴沃克),在此过程中做过的好事可谓数不胜数,罄竹难书,我们来按着时间线整理一下 1一开始的玛丽苏是个渴望母爱的孩子,尽管我们不知道bs设定下一开始的支配者到底会不会有类似人类的亲情,她掌管自己的世界,倾听子民的祈祷,开始感到厌烦,这时贾巴沃克不知出于什么目的,送了她一本童话书,这本书,我们不知道是哪个童话,但本人猜测很可能这本书的作者是玛丽苏第一个抓住的,并在黑之魂的融合中有重要地位,根据青鸟的文本,卡罗尔并不是第一个抓住的素材,所以基本可以排除梦游仙境,结合男主角格林的名字和混沌迷宫的狼外婆,我个人猜测是小红帽,她开始渴望创作自己的故事来打动母亲,至少一开始是这样,她派遣属下四处收集童话作者的灵魂作为素材,同时肆意进行同人创作。 2玛丽苏的处女作是小红帽,也是她第二得意的作品,根据一些信息,小红帽的灵魂可能以现实世界的一个女学生为素材,在魔改剧情的同时,她还给了小红帽注定20岁早逝的设定,并可能赋予了小红帽通过镜子穿梭位面之类的特殊能力来担任女主角,但不知道为什么她又不满意,想做一个男主角出来,但她对小红帽的善后却颇有些问题,小红帽不仅杀穿了红森,而且还能意识到她这个黑幕的存在。 3缝合了众多童话作家灵魂的格林诞生了,并被赋予了给周围的女主角带来不幸的设定,格林污秽的黑之魂有成为支配者的潜质,玛丽苏甚至还大胆地保留了他的部分创作能力,因为最关键的改变权能在她手上,为什么叫做格林则未知,可能是最初的童话书就是格林童话的一本,这之后格林不知道为什么,以什么身份在一个叫不思议之国的地方和叫爱丽丝和祈祷主的存在开起了茶会,随后格林与爱丽丝01相恋,嫉妒的祈祷主呼唤了玛丽苏,导致格林被带走了,连同格林不知何时创造出的故事们也被篡改 4基于以上提到的各种童话故事素材,玛丽苏魔改出了失落帝国的箱庭,把格林放进去经历一次次绝望故事的轮回,自己则担任女主角欣赏故事,还设计把母亲叫了进来欣赏自己的大作。不知多少次循环后,这个大好局面被打破了,母亲黑山羊为了逃离这个世界和她战斗,连圣森都磨灭了,战胜母亲后,奈亚丽丝前来捡漏带走格林进行新一轮追寻爱的游戏,本来想顺带着把玛丽苏也灭了,但在诺登的劝阻以及可能的其他考量下放过了她 5奈亚,红女王,白女王中的某位或若干位剥夺了她的改变权能,把她囚禁在库因兰德,失去权能的她改名为玛丽安,但不知何时也不知何人前来探访了她,到格林试图从梦中醒来的里线,玛丽安乘乱逃出,由于正史上不太可能发生f结局,所以此时应该是g结局,也有可能正史上g结局有少许与游戏不同,不管怎么说此时的玛丽安应该被格林小红帽两人打败,但h结局中可以看到她没有死,而且不知道怎么逃了出来 可以说,bs中的一切悲剧,玛丽苏至少有五成功劳,接下来让我们来分析一下玛丽苏的角色特质。 首先,最直接的一点,玛丽苏是个典型的支配者,高高在上地支配着人类这样的低等种族,但玛丽苏特殊之处在于,她可能是最能理解人类感情的支配者之一,首先我们就可以看到她居然渴望所谓的母爱,而根据2代大部分支配者的表现,即使因融入皮套逐渐有了感情,也没有第二个有亲情这种非常类似人类感情的支配者,此外,她还以玩弄人类的灵魂为乐,当然有这种兴趣的支配者恐怕不少,但这股风气可以说是玛丽苏带起来的,也是她最先玩出各种花样。 因此可以引出玛丽苏的第二个特点了,她是很像人类的一个支配者,尽管理解非常片面,但她确实懂得并拥有不少人性,而她为什么这么喜欢玩弄人类呢?这也很容易理解,一般来说越通人性的动物越被人类亲近,逗猫逗狗远远比逗蚂蚁有意思,因为这些宠物的智力和人类更接近,人类可以很容易地理解它们在想什么,然后在逗弄它们的过程中获得一种智力上的优越感,以及一种“支配感”,这恐怕就是玛丽苏看到自己编排的好戏上演的感觉。 这点可以说是我们对玛丽苏进行解析的基石,毕竟任何角色首先都是人的投影,而人性越丰富,就有越多的性格侧面。 玛丽苏第三个特点就是由此衍生的纯粹性,当然,此处并不是说纯洁善良云云,而是某种意义上的纯粹之恶,很多支配者在扮演人类后都会被皮套影响而恐慌或纠结,但玛丽苏却没有这种烦恼,她以融入人类扮演人类为乐(小精灵也算类人种族),她作为支配者的漆黑本性和人性之恶完美地兼容了,不会有徘徊二者之间的身份认同问题,而她大部分所作所为也就是为了践行人性之恶,什么是恶呢,比较狭隘的解释就是为了为了自己的利益或者取乐而伤害他人,而玛丽苏的邪恶就很纯粹,就是为了取乐,甚至有损自己利益也要作恶,如果解救了被囚禁的玛丽苏,此时她会自认为东山再起,但她想的不是第一时间抹杀已经成长了的格林或者藏起来,而是想再让格林经历一次悲惨的故事,可以说她作恶的动机相当纯粹,也相当执着。 在此之上的第四个特点,就是她的创作者身份,很多支配者都会赞扬她的创作能力,连奈亚构建的不思议之国都有不少玛丽苏箱庭的影子,但这种创造力也只是对于支配者来说了,如果我们用人类的视角看如何呢?寿司在访谈时轻蔑地说到“她说到底也只是玛丽苏,也只能整点二次创作了”可以说道出了玛丽苏所谓创作的本质,说到底,玛丽苏就是那种典型的黑深残小鬼,把一个可能有很多种解释的作品曲解为单一的猎奇世界观,当然不是说这样不行,如果原创一个黑深残世界观自娱自乐当然是可以接受的,但玛丽苏的行为就是最恶劣的一种同人女行为,魔改原来的作品,把自己做成角色代入进去搞cp,还要把所有其他角色踩一遍,情节和人物关系只要对自己代入的角色有利就行,然后把这部除了自己看谁也不会喜欢的同人拿给原作者看,我就不详细说这种行为的恶劣程度了,但这种作品折射出来的创作观我必须要辩驳一下。 当然,本视频所有讨论只局限于二次元文化内, 荒木飞吕彦认为漫画有四要素,角色、剧情、世界观、主题,我们就用这四个维度来剖析玛丽苏的所谓创作。 首先是角色,直接创作一个鲜活的灵魂对强大的支配者来说也是一件难事,所以对于角色的选取,玛丽苏很可能都是使用现实存在的灵魂然后再魔改来适配进童话或者传说的人物,因此她笔下所谓角色虽然很多但其实并不是她自己的功劳,而她为了把这些灵魂塞进角色对设定随意删改,把小红帽的外婆和母亲缝成了一笔烂账,人物关系更是一团乱麻,怎么方便怎么来,角色设定连基本的自洽也做不到,水平着实不敢恭维 随后是世界观,失落帝国这个箱庭本质上来说就是个童话故事的缝合体,没有历史演化,没有详细设定,这并不是一个鲜活的世界观,只不过是一个临时搭建的舞台而已,当然,很多线性的故事并不需要一个多详尽的世界观,在这点上玛丽苏只能说无功无过 最后是剧情和主题,玛丽苏的主题是简单粗暴的黑深残,剧情则是当常规的rpg剧本演到最后的happy end时毫无铺垫伏笔地急转直下变成bad end,当然,能设置这么大规模的箱庭,还写了不少支线剧情,证明玛丽苏确实是有一些笔力的,但首先,她的角色基本靠抓人,故事则都有童话原型,故事演变她只需要把握大方向,其他可以让角色自己来,而最后没有任何铺垫的bad end依旧表明了她创作的失败,如果一个设定没有任何铺垫和暗示,直到使用时才抛出,那只能证明这部作品情节编排的失败,因为一部作品的生命周期不是作者创作出来就结束了的,而要等到读者看完理解了故事才会结束,这个过程作者读者应该处于相对公平的地位,根据故事的设定,人物有充分的理由这样行动,这样才能让读者认同这个故事,而玛丽苏却完全相反,滥用作者的权能让故事不仅没有逻辑,还自相矛盾,很明显,对玛丽苏来说她是作者也自认为是唯一的读者,那些被抓走被改造的灵魂不过是用完即扔的工具罢了,不需要自圆其说,只要自己看得高兴就行了,或许就支配者的立场来说她不过是自娱自乐罢了,但对人类(至少灵魂上是人类),以及同样作为创作者的格林来说,首先就绝不可能认同这种恶行,更不可能认同自己的作品被改成这样的烂作 说到这里,就可以讨论一下玛丽苏对于格林的看法了,直观地说,是玛丽苏创造了名为格林的污秽黑之魂,但其实在最初,是格林等童话作家激发了玛丽苏的创作欲,因此,事实上,两者是相互创造的关系,玛丽苏创造格林的目的,首先是为了成为她作品的男主角,让她能够代入女主角的位置欣赏这个故事,这样说来似乎格林除了男主角的身份和其他角色也没什么本质的不同。但格林还有一点对玛丽苏有着重大意义,就是他童话作家灵魂集合体的身份,即使自我中心如玛丽苏这种存在,也会有对别人欣赏自己作品的渴望,因此玛丽苏特地设置了一个c结局,用演戏的形式让格林得以了解她的整个创作生涯,至于目的,除了单纯的表现欲和欣赏格林的痛苦以外,恐怕也有一丝希望作为原作者的格林认同自己的心情,哪怕是厌恶,玛丽苏也想得到一些对创作的反馈,而格林是唯一能在创作这个领域和她有一些共鸣的人,作者,读者,男主角,格林三位一体的身份对玛丽苏来说,可以说是难得的知己,尽管这种关系非常扭曲,但不能否认,在这点上玛丽苏作为创作者的心情是有些真心的。而玛丽苏会渴望认同这点,一开始是希望得到母爱,但在得到格林这个玩具之后,玛丽苏就一点也不在意黑山羊的死活了,这也是佐证。 最后不得不提的是,玛丽苏的特殊性质,很大程度上她是寿司这个作者的投影,我个人觉得玛丽苏这个角色有不少表达寿司自己创作观的成分,这也解释了寿司为何这么偏爱她当然,一部好的作品,任何角色都是基于自己的设定和世界观行动,不可能因为是作者的投影就有特别待遇,所以可以说,玛丽苏虽然很大程度上是寿司的投影,但投影的目的其实是对比,玛丽苏的创作肤浅,笔下的故事只是无聊的黑深残,但寿司却喜欢在绝望时写一些希望,在希望中铺设绝望,最后的反转再怎么说都是有因可循,单论创作的层次来说就高出绿虫子太多了,当然,我也不是在吹寿司笔力多高,因为高出玛丽苏这个水平的创作者多如牛毛。 寿司设置玛丽苏这个角色,其实是使用了一种嵌套的结构来讲故事,首层是童话的原作,这些是毋庸置疑的好故事,随后是虫子和奈亚魔改出的箱庭,是烂故事的典型,最后一层寿司想讲的重点其实是格林怎么察觉真相,挣脱出烂故事的循环,书写自己的结局的故事,在这三层中,第一层玛丽苏是读者,格林等人是作者,只出现在设定层面,第二层玛丽苏是一半作者一半角色,格林是一半读者一半角色,体现在abc结局,最后一层中寿司是唯一的作者,玛丽苏和格林就都是角色了,体现在d结局以及之后的二代,这种层层演变虽然有些炫技,但确实非常有意思。 就玛丽苏这个角色而言,整个泛二次元文化里她这样的反派也不常见,究其原因,则是因为一个有能力玩弄主角取乐的boss必然会导致战力失衡,冲突不起来,让读者感到憋屈,因此想要打败这种boss要么机械降神唯心爆发,比如一代c结局(虽然是演的),要么引入新的boss和同伴体系取代她如d结局,也因此,虽然我个人很喜欢一代,但一代的真结局d结局远没有2代h结局震撼 来做个总结吧,玛丽苏无疑是个纯粹邪恶的支配者,一个烂到骨子里的创作者,她作为创作者无疑是失败的,但作为bs这个故事里的角色反而是很成功的,不仅纯粹有特点,还有很多角色侧面可以挖掘,寿司巧妙地利用她读者,创作者和角色的三重身份来塑造她的多面性,颇有荒木在漫画术中写的“在作恶道路上高歌猛进”的成功反派角色风格。

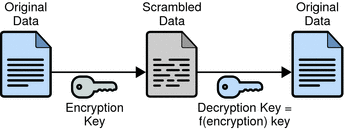 安全性是指在面对攻击时保持系统按预期运行 这可以采取多种形式:
安全性是指在面对攻击时保持系统按预期运行 这可以采取多种形式: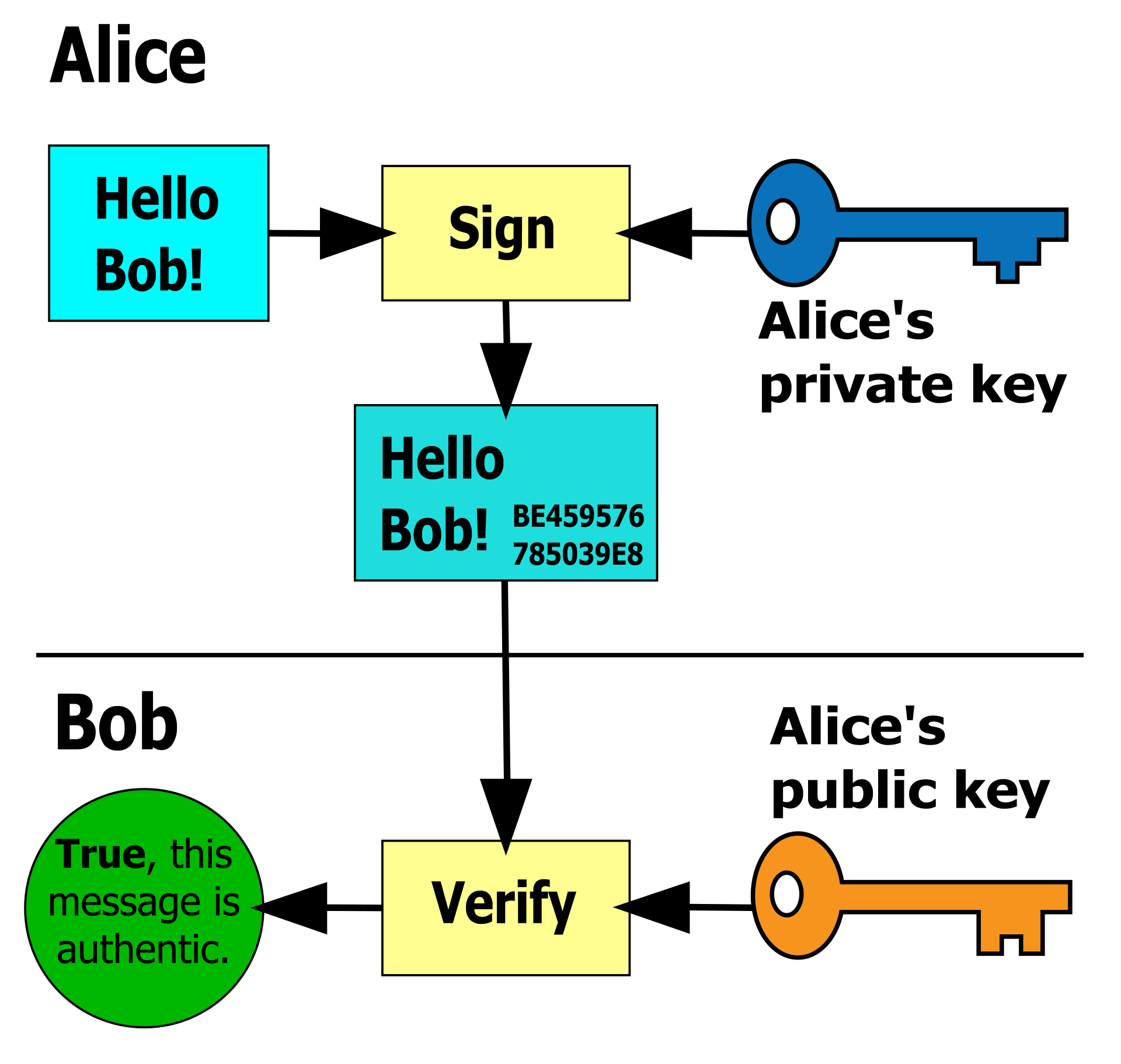
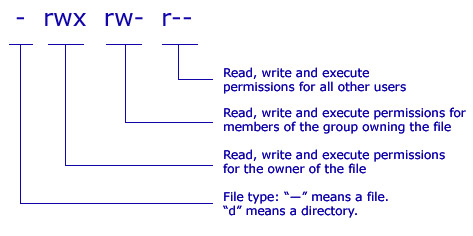


 CPU与外设之间的数据交换必须通过接口来完成,通常接口有
CPU与外设之间的数据交换必须通过接口来完成,通常接口有 机器数的表示形式:原码、反码、补码
机器数的表示形式:原码、反码、补码 – 4个通用寄存器(16位)
– 4个通用寄存器(16位) 为什么这种层次化结构是有效的?
为什么这种层次化结构是有效的?