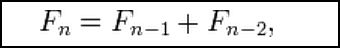Skip to content

Latest commit

 

History

History
176 lines (128 loc) · 4.36 KB

README.md

File metadata and controls

176 lines (128 loc) · 4.36 KB
Raw

Recursion Review

This repo is a work in progress with resources to learn recursion. Have questions or feedback? Get in touch with me on Twitter, @valeriecodes or via email at valerie.woolard@gmail.com

What is recursion?

Solving a problem by solving smaller versions of the same problem. A recursive function is one that calls itself.

One mathematical practice that mirrors the structure of a recursive function is an inductive proof. If you've used this, a lot of these concepts may be familiar to you.

In an inductive proof, you can prove that something is true for all natural numbers N by proving that:

  • It is true for the first natural number (0 or 1) (this is called the basis or base case)
  • It is true for arbitrary natural number n and n + 1 (this is called the inductive step)

By the same token, a recursive function has:

  • A base case. This is a defined solution that will not call the function again. (This is where the function stops.)
  • A reduction step. This relates the problem to a smaller subproblem of the same function. (Converges to the base case enventually)

Fun with recursion

Google easter egg: Recursion!

Let's think about writing a recursive program that performs a simple countdown.

What is the base case? What is the reduction step?

Method signature:

def countdown(n):
  # method body goes here

10 minutes for working. Want to use Python? Try http://www.skulpt.org/

Desired output

>>> countdown(10)
10
9
8
7
6
5
4
3
2
1
BLASTOFF!

Go over the solutions together.

Pitfalls

  • Make sure that you have a base case and that you will always hit it. Otherwise the program will loop infinitely.
    • What's wrong here?
      def countdown(n):
    if n == 0:
      print "BLASTOFF!"
    else:
      print n
      countdown(n-1)
  • Make sure that your problem is actually getting smaller each time.

Next problem: Factorial

Remember these? https://en.wikipedia.org/wiki/Factorial

3! = 3 * 2 * 1

5! = 5 * 4 * 3 * 2 * 1

And so on...

Let's write it. What is the base case? What is the reduction step?

###Method signature:

def factorial(n):
  # method body goes here

Let's spend 10 minutes on this. Let's not worry about negative numbers for now. Need that site again? It's http://www.skulpt.org/

Desired output

>>> factorial(5)
120

Next up: Fibonacci Sequence

Fibonacci Sequence formula

Write a function that returns the nth Fibonacci number. Base case? Reduction step?

Method signature:

def fibonacci(n):
  # method body goes here

Remember: fibonacci(0) is 0 and fibonacci(1) is 1

Let's spend 10 minutes on this.

Desired output

>>> fibonacci(6)
8

What about really big inputs?

Other pitfalls

  • Redundant calculations
  • Stack overflows

Binary search

Given a sorted array and a number, write a recursive function that returns true if the number is in the array and false if not.

Base case? Reduction step?

Method signature:

def search(arr, n):
  # method body goes here

15 minutes to work.

Desired output

>>> search([1, 2, 3], 3)
True
>>> search([1, 2, 3], 5)
False

Other things to know:

  • Iterative approaches
  • Memoization/dynamic programming

Iteration in mathematics may refer to the process of iterating a function i.e. applying a function repeatedly, using the output from one iteration as the input to the next.

Recursive functions are often easier to write with iteration. Simply put, an iteration is a for-loop.

Countdown program in iterative form

def countdown(n):
  for i in range(n, 0, -1):
    print i
  print 'BLASTOFF!'

Exercise if we have time: rewrite previous functions with iteration.

Resources:

http://introcs.cs.princeton.edu/java/23recursion/

https://en.wikipedia.org/wiki/Recursion_(computer_science)

https://www.khanacademy.org/computing/computer-science/algorithms/recursive-algorithms/a/recursion

https://en.wikipedia.org/wiki/Mathematical_induction