许多数据集从从本质上是嵌套结构的。考虑在 geographic entities 应用场景中,比如人口普查,人口结构以及国家和州;企业和政府的组织结构;文件系统和软件包。甚至非层级的数据也可以被组合成层级数据结构,比如 k-means clustering(k - means 聚类) or phylogenetic trees (生态系统树)。
这个模块实现了几种经典的对层次结构数据的可视化技术:
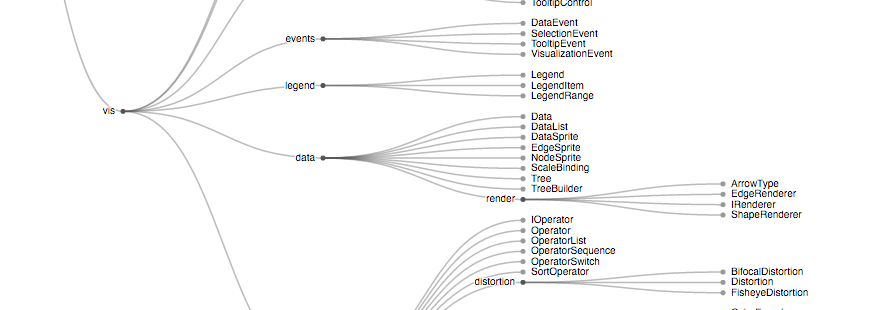
Node-link diagrams(节点-链接图) 对节点和边使用离散的标记来展示拓扑结构,比如节点展示为圆并且父子节点之间使用线连接。“tidy” tree 结构更紧密,而 dendrogram(系统树) 则将所有的叶节点放置在同一水平线上。(它们都有极坐标系和笛卡尔坐标系两种形式。) Indented trees(缩进树) 对交互式展示很有用。
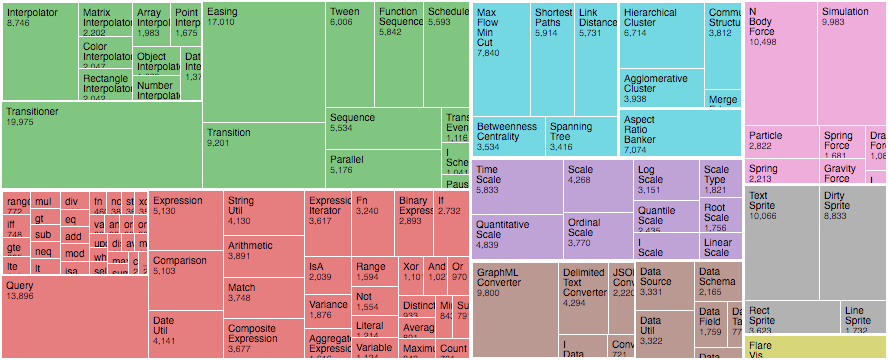
Adjacency diagrams(邻接图) 使用节点的相对位置展示拓扑结构。这种展示方式将每个节点编码为定量的区域,比如使用区域大小表示收入或文件大小。“icicle” diagram 使用矩形表示区域,而 “sunburst” 则使用分段环形图来表示。
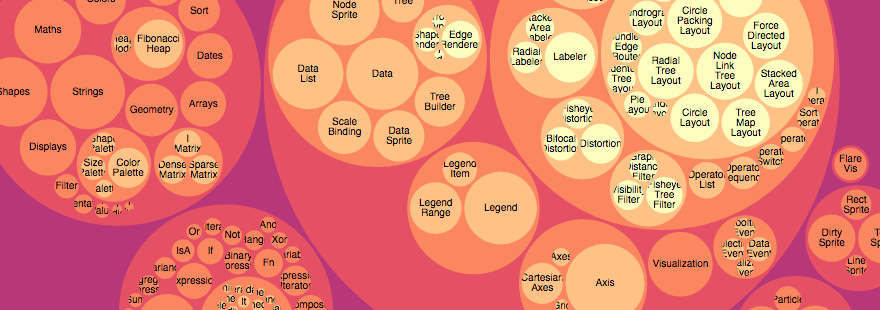
Enclosure diagrams(包裹图) 也是一种区域编码,但是通过相互包含的形式来展示拓扑结构。treemap 递归的将一个区域划分为更小的矩形区域。Circle-packing 则通过相互紧凑嵌套的圆来表示, 虽然空间利用率不高,但是能更明显的展示拓扑结构。
一个好的层次结构可视化能促进快速的促进多尺度推理: 对单个单元的微观观察和对整体的宏观观察.
NPM 安装:npm install d3-hierarchy. 此外还可以下载 latest release. 可以直接从 d3js.org 以 standalone library 或作为 D3 4.0 的一部分直接载入. 支持 AMD, CommonJS 和基础的标签引入形式,如果使用标签引入则会暴露 d3 全局变量:
<script src="https://d3js.org/d3-hierarchy.v1.min.js"></script>
<script>
var treemap = d3.treemap();
</script>在计算层次布局之前,你需要一个根节点。如果你的数据已经是层次结构,比如 JSON。你可以直接将其传递给 d3.hierarchy; 此外,你可以重新排列扁平数据,比如将 CSV 使用 d3.stratify 重组为层次结构数据。
# d3.hierarchy(data[, children]) <源码>
根据指定的层次结构数据构造一个根节点。指定的数据 data 必须为一个表示根节点的对象。比如:
{
"name": "Eve",
"children": [
{
"name": "Cain"
},
{
"name": "Seth",
"children": [
{
"name": "Enos"
},
{
"name": "Noam"
}
]
},
{
"name": "Abel"
},
{
"name": "Awan",
"children": [
{
"name": "Enoch"
}
]
},
{
"name": "Azura"
}
]
}指定的 children 访问器会为每个数据进行调用,从根 data 开始,并且必须返回一个数组用以表示当前数据的子节点,返回 null 表示当前数据没有子节点。如果没有指定 children 则默认为:
function children(d) {
return d.children;
}返回的节点和每一个后代会被附加如下属性:
- node.data - 关联的数据,由 constructor 指定.
- node.depth - 当前节点的深度, 根节点为
0. - node.height - 当前节点的高度, 叶节点为
0. - node.parent - 当前节点的父节点, 根节点为
null. - node.children - 当前节点的孩子节点(如果有的话); 叶节点为
undefined. - node.value - 当前节点以及 descendants(后代节点) 的总计值; 可以通过 node.sum 和 node.count 计算.
这个方法也可以用来测试一个节点是否是 instanceof d3.hierarchy 并且可以用来扩展节点原型链。
返回祖先节点数组,第一个节点为自身,然后依次为从自身到根节点的所有节点。
返回后代节点数组,第一个节点为自身,然后依次为所有子节点的拓扑排序。
返回叶节点数组,叶节点是没有孩子节点的节点。
返回从当前 node 到指定 target 节点的最短路径。路径从当前节点开始,遍历到当前 node 和 target 节点共同最近祖先,然后到 target 节点。这个方法对 hierarchical edge bundling(分层边捆绑) 很有用。
返回当前 node 的 links 数组, 其中每个 link 是一个定义了 source 和 target 属性的对象。每个 link 的 source 为父节点, target 为子节点。
从当前 node 开始以 post-order traversal 的次序为当前节点以及每个后代节点调用指定的 value 函数,并返回当前 node。这个过程会为每个节点附加 node.value 数值属性,属性值是当前节点的 value 值和所有后代的 value 的合计,函数的返回值必须为非负数值类型。value 访问器会为当前节点和每个后代节点进行评估,包括内部结点;如果你仅仅想让叶节点拥有内部值,则可以在遍历到叶节点时返回 0。例如 这个例子,使用如下设置等价于 node.count:
root.sum(function(d) { return d.value ? 1 : 0; });在进行层次布局之前必须调用 node.sum 或 node.count,因为布局需要 node.value 属性,比如 d3.treemap。API 支持方法的 method chaining (链式调用), 因此你可以在计算布局之前调用 node.sum 和 node.sort, 随后生成 descendant nodes 数组, 比如:
var treemap = d3.treemap()
.size([width, height])
.padding(2);
var nodes = treemap(root
.sum(function(d) { return d.value; })
.sort(function(a, b) { return b.height - a.height || b.value - a.value; }))
.descendants();这个例子假设 node 数据包含 value 字段.
计算当前 node 下所有叶节点的数量,并将其分配到 node.value 属性, 同时该节点的所有后代节点也会被自动计算其所属下的所有叶节点数量。如果 node 为叶节点则 count 为 1。该操作返回当前 node。对比 node.sum。
以 pre-order traversal 的次序对当前 node 以及其所有的后代节点的子节点进行排序,指定的 compare 函数以 a 和 b 两个节点为参数。返回当前 node。如果 a 在 b 前面则应该返回一个比 0 小的值,如果 b 应该在 a 前面则返回一个比 0 大的值,否则不改变 a 和 b 的相对位置。参考 array.sort 获取更多信息。
与 node.sum 不同,compare 函数传递两个 nodes 实例而不是两个节点的数据。例如,如果数据包含 value 属性,则根据节点以及此节点所有的后续节点的聚合值进行降序排序,就像 circle-packing 一样:
root
.sum(function(d) { return d.value; })
.sort(function(a, b) { return b.value - a.value; });类似的,按高度降序排列 (与任何后代的距离最远) 然后按值降序排列,是绘制 treemaps 和 icicles 的推荐排序方式:
root
.sum(function(d) { return d.value; })
.sort(function(a, b) { return b.height - a.height || b.value - a.value; });先对高度进行降序,然后按照 id 进行升序排列,是绘制 trees 和 dendrograms 的推荐排序方式:
root
.sum(function(d) { return d.value; })
.sort(function(a, b) { return b.height - a.height || a.id.localeCompare(b.id); });如果想在可视化布局中使用排序,则在调用层次布局之前,必须先调用 node.sort;参考 node.sum。
以 breadth-first order(广度优先) 的次序为每个 node 调用执行的 function, 一个给定的节点只有在比其深度更小或者在此节点之前的相同深度的节点都被访问过之后才会被访问。指定的函数会将当前 node 作为参数。
# node.eachAfter(function) <源码>
以 post-order traversal(后序遍历) 的次序为每个 node 调用执行的 function,当每个节点被访问前,其所有的后代节点都已经被访问过。指定的函数会将当前 node 作为参数。
# node.eachBefore(function) <源码>
以 pre-order traversal(前序遍历) 的次序为每个 node 调用执行的 function,当每个节点被访问前,其所有的祖先节点都已经被访问过。指定的函数会将当前 node 作为参数。
以当前节点 node 为根节点,返回子树的深拷贝副本。(但是副本与当前子树仍然共享同一份数据)。当前节点为返回子树的根节点,返回的节点的 parent 属性总是 null 并且 depth 总是 0.
考虑如下关系的列表:
| Name | Parent |
|---|---|
| Eve | |
| Cain | Eve |
| Seth | Eve |
| Enos | Seth |
| Noam | Seth |
| Abel | Eve |
| Awan | Eve |
| Enoch | Awan |
| Azura | Eve |
这些名称时独一无二的,因此我们可以将上述表示层级数据的列表表示为 CSV 文件:
name,parent
Eve,
Cain,Eve
Seth,Eve
Enos,Seth
Noam,Seth
Abel,Eve
Awan,Eve
Enoch,Awan
Azura,Eve
解析 CSV 使用 d3.csvParse:
var table = d3.csvParse(text);然后返回:
[
{"name": "Eve", "parent": ""},
{"name": "Cain", "parent": "Eve"},
{"name": "Seth", "parent": "Eve"},
{"name": "Enos", "parent": "Seth"},
{"name": "Noam", "parent": "Seth"},
{"name": "Abel", "parent": "Eve"},
{"name": "Awan", "parent": "Eve"},
{"name": "Enoch", "parent": "Awan"},
{"name": "Azura", "parent": "Eve"}
]转为层次结构数据:
var root = d3.stratify()
.id(function(d) { return d.name; })
.parentId(function(d) { return d.parent; })
(table);返回:
此时的层次数据才可以被传递给层次布局来可视化,比如 d3.tree.
使用默认的配置构造一个新的 stratify(分层) 操作。
根据执行的扁平 data 生成一个新的层次结构数据.
如果指定了 id, 则将 id 访问器设置为指定的函数并返回分层操作。否则返回当前的 id 访问器, 默认为:
function id(d) {
return d.id;
}id 访问器会为每个输入到 stratify operator 的数据元素进行调用,并传递当前数据 d 以及当前索引 i. 返回的字符串会被用来识别节点与 parent id(父节点 id) 之间的关系。对于叶节点,id 可能是 undefined; 此外 id 必须是唯一的。(Null 和空字符串等价于 undefined).
# stratify.parentId([parentId]) <源码>
如果指定了 parentId,则将当前父节点 id 访问器设置为给定的函数,并返回分层操作。否则返回当前父节点 id 访问器, 默认为:
function parentId(d) {
return d.parentId;
}父节点 id 访问器会为每个输入的元素进行调用,并传递当前元素 d 以及当前索引 i. 返回的字符串用来识别节点与 id 的关系。对于根节点, 其父节点 id 应该为 undefined。(Null 和空字符串等价于 undefined)。输入数据必须有一个根节点并且没有循环引用关系。
cluster layout 布局用来生成 dendrograms(系统树):节点-连接图中所有的叶节点都放在相同的深度上。Dendograms 通常不如 tidy trees 紧凑,但是当所有的叶子都在同一水平时是有用的,比如分层聚类或 phylogenetic tree diagrams(系统树图)。
使用默认的配置创建一个新的系统树布局.
对指定的 root hierarchy 进行布局,并为 root 以及它的每一个后代附加两个属性:
- node.x - 节点的 x- 坐标
- node.y - 节点的 y- 坐标
节点的 x 和 y 坐标可以是任意的坐标系统;例如你可以将 x 视为角度而将 y 视为半径来生成一个 radial layout(径向布局)。你也可以在布局之前使用 root.sort 进行排序操作。
如果指定了 size 则设置当前系统树布局的尺寸为一个指定的二元数值类型数组,表示 [width, height] 并返回当前系统树布局。如果 size 没有指定则返回当前系统树布局的尺寸,默认为 [1, 1]。如果返回的布局尺寸为 null 时则表示实际的尺寸根据 node size 确定。坐标 x 和 y 可以是任意的坐标系统;例如如果要生成一个 radial layout(径向布局) 则可以将其设置为 [360, radius] 用以表示角度范围为 360° 并且半径范围为 radius。
# cluster.nodeSize([size]) <源码>
如果指定了 size 则设置系统树布局的节点尺寸为指定的数值二元数组,表示为 [width, height] 并返回当前系统树布局。如果没有指定 size 则返回当前节点尺寸,默认为 null。如果返回的尺寸为 null 则表示使用 layout size 来自动计算节点大小。当指定了节点尺寸时,根节点的位置总是位于 ⟨0, 0⟩。
# cluster.separation([separation]) <源码>
如果指定了 seperation, 则设置间隔访问器为指定的函数并返回当前系统树布局。如果没有指定 seperation 则返回当前的间隔访问器,默认为:
function separation(a, b) {
return a.parent == b.parent ? 1 : 2;
}间隔访问器用来设置相邻的两个叶节点之间的间隔。指定的间隔访问器会传递两个叶节点 a 和 b,并且必须返回一个期望的间隔值。这些节点通常是兄弟节点,如果布局将两个节点放置到相邻的位置,则可以通过配置间隔访问器设置相邻节点之间的间隔控制其期望的距离。
tree 布局基于 Reingold–Tilford “tidy” algorithm 用来生成节点-链接树,由 Buchheim et al. 等人进行了时间上的优化,紧凑树布局比 dendograms 空间上看来更紧凑。
使用默认的设置创建一个新的树布局。
对指定的 root hierarchy 进行布局,并为 root 以及它的每一个后代附加两个属性:
- node.x - 节点的 x- 坐标
- node.y - 节点的 y- 坐标
节点的 x 和 y 坐标可以是任意的坐标系统;例如你可以将 x 视为角度而将 y 视为半径来生成一个 radial layout(径向布局)。你也可以在布局之前使用 root.sort 进行排序操作。
如果指定了 size 则设置当前系统树布局的尺寸为一个指定的二元数值类型数组,表示 [width, height] 并返回当前树布局。如果 size 没有指定则返回当前系统树布局的尺寸,默认为 [1, 1]。如果返回的布局尺寸为 null 时则表示实际的尺寸根据 node size 确定。坐标 x 和 y 可以是任意的坐标系统;例如如果要生成一个 radial layout(径向布局) 则可以将其设置为 [360, radius] 用以表示角度范围为 360° 并且半径范围为 radius。
如果指定了 size 则设置系统树布局的节点尺寸为指定的数值二元数组,表示为 [width, height] 并返回当前树布局。如果没有指定 size 则返回当前节点尺寸,默认为 null。如果返回的尺寸为 null 则表示使用 layout size 来自动计算节点大小。当指定了节点尺寸时,根节点的位置总是位于 ⟨0, 0⟩。
# tree.separation([separation]) <源码>
如果指定了 seperation, 则设置间隔访问器为指定的函数并返回当前树布局。如果没有指定 seperation 则返回当前的间隔访问器,默认为:
function separation(a, b) {
return a.parent == b.parent ? 1 : 2;
}一种更适合于径向布局的变体,可以按比例缩小半径差距:
function separation(a, b) {
return (a.parent == b.parent ? 1 : 2) / a.depth;
}间隔访问器用来设置相邻的两个节点之间的间隔。指定的间隔访问器会传递两个节点 a 和 b,并且必须返回一个期望的间隔值。这些节点通常是兄弟节点,如果布局将两个节点放置到相邻的位置,则可以通过配置间隔访问器设置相邻节点之间的间隔控制其期望的距离。
参考 1991年 Ben Shneiderman 的介绍,treemap 根据每个节点的值递归的将区域划分为矩形。D3 的 treemap 的实现支持可扩展的 tiling method(铺设方法):默认的 squarified 方法生成的矩形长宽比例遵从 golden(黄金比例);此外还提供了比 slice-and-dice 更具有可读性和尺寸估计的铺设方法,也就是只在水平或者垂直方向按照深度划分。
# d3.treemap()
使用默认的配置创建一个新的 treemap 布局。
对指定的 root hierarchy 进行布局,为 root 以及每个后代节点附加以下属性:
- node.x0 - 矩形的左边缘
- node.y0 - 矩形的上边缘
- node.x1 - 矩形的右边缘
- node.y1 - 矩形的下边缘
在将层次数据传递给 treemap 布局之前,必须调用 root.sum。在计算布局之前还可能需要调用 root.sort 对节点进行排序。
如果指定了 tile 则设置 tiling method 为指定的函数并返回当前 treemap 布局。如果没有指定 tile 则返回当前铺设方法,默认为 d3.treemapSquarify,也就是切分的矩形的长宽比遵循黄金比例。
如果指定了 size 则将当前的布局尺寸设置为指定的二元数值数组:[width, height],并返回当前 treemap 布局。如果没有指定 size 则返回当前尺寸,默认为 [1, 1]。
如果指定了 round 则根据指定的布尔类型值启用或禁用四舍五入,并返回当前 treemap 布局。如果 round 没有指定则返回当前 rounding 状态,默认为 false。
# treemap.padding([padding]) <源码>
如果指定了 padding 则同时设置 inner 和 outer 间隔为指定的数值或函数,并返回当前 treemap 布局。如果没有指定 padding 则返回当前的 inner 间隔函数。
# treemap.paddingInner([padding]) <源码>
如果指定了 padding 则将当前 inner 间隔设置为指定的数值或函数并返回当前的 treemap 布局。如果 padding 没有指定则返回当前 inner 间隔函数,默认为常数 0。如果 padding 为函数则会为每个包含子节点的节点调用并传递当前节点。inner 间隔用来设置节点相邻两个子节点之间的间隔。
# treemap.paddingOuter([padding]) <源码>
如果指定了 padding 则将 top, right, bottom 和 left 间隔设置为指定的数值或函数,并返回当前 treemap 布局,如果没有指定 padding 则返回当前 top 间隔函数。
# treemap.paddingTop([padding]) <源码>
如果指定了 padding 则将 top 间隔设置为指定的数值或函数并返回当前 treemap 布局。如果没有指定 padding 则返回当前 top 间隔函数,默认为常量 0。如果 padding 为会为每个包含子节点的节点调用并传递当前节点。top 间隔用来将节点的顶部边缘与其子节点分开。
# treemap.paddingRight([padding]) <源码>
如果指定了 padding 则将 right 间隔设置为指定的数值或函数并返回当前 treemap 布局。如果没有指定 padding 则返回当前 right 间隔函数,默认为常量 0。如果 padding 为会为每个包含子节点的节点调用并传递当前节点。right 间隔用来将节点的右侧边缘与其子节点分开。
# treemap.paddingBottom([padding]) <源码>
如果指定了 padding 则将 bottom 间隔设置为指定的数值或函数并返回当前 treemap 布局。如果没有指定 padding 则返回当前 bottom 间隔函数,默认为常量 0。如果 padding 为会为每个包含子节点的节点调用并传递当前节点。bottom 间隔用来将节点的下侧边缘与其子节点分开。
# treemap.paddingLeft([padding]) <源码>
如果指定了 padding 则将 left 间隔设置为指定的数值或函数并返回当前 treemap 布局。如果没有指定 padding 则返回当前 left 间隔函数,默认为常量 0。如果 padding 为会为每个包含子节点的节点调用并传递当前节点。left 间隔用来将节点的左侧边缘与其子节点分开。
几种内置的铺设方法,用来供 treemap.tile 使用。
# d3.treemapBinary(node, x0, y0, x1, y1) <源码>
递归地将指定的 nodes 划分为一个近似平衡的二叉树,宽矩形进行水平分割和高矩形进行垂直分割。
# d3.treemapDice(node, x0, y0, x1, y1) <源码>
将通过指定 x0, y0, x1, y1 所指定的矩形区域按指定节点的每个子节点的值水平分割. 子节点按顺序排列, 从给定矩形的左边缘 (x0) 开始. 如果子节点值的和小于指定节点值(比如指定的节点具有非零的内部值), 剩余的空白将定位在给定矩形的右边缘 (x1).
# d3.treemapSlice(node, x0, y0, x1, y1) <源码>
将通过指定 x0, y0, x1, y1 所指定的矩形区域按指定节点的每个子节点的值垂直分割. 子节点按顺序排列, 从给定矩形的上边缘 (y0) 开始. 如果子节点值的和小于指定节点值(比如指定的节点具有非零的内部值), 剩余的空白将定位在给定矩形的下边缘 (y1).
# d3.treemapSliceDice(node, x0, y0, x1, y1) <源码>
如果指定的节点深度为奇数, 则使用 treemapSlice 算法; 否则使用 treemapDice 算法.
# d3.treemapSquarify(node, x0, y0, x1, y1) <源码>
实现了由 Bruls et al. 等人提出的 squarified treemap,这种铺设方法会尽可能的使用指定的 aspect ratio(纵横比)) 来切分矩形。
# d3.treemapResquarify(node, x0, y0, x1, y1) <源码>
与 d3.treemapSquarify 类似, 除了保存 d3.treemapResquarify 计算的前一个布局的拓扑(节点邻接)外, 如果有拓扑则使用相同的 target aspect ratio. 这种平铺方法很适合对矩阵树图的更改进行动画处理, 因为它只更改节点大小, 而不更改它们的相对位置, 从而避免了分散注意力的移动和遮挡. 但是也有缺点, 后续的更新布局可能不够理想: 只有第一次布局使用 Bruls 等人的平方算法.
指定期望矩形的纵横比。ratio 必须为大于等于 1 的数值。请注意,生成的矩形(高或宽)的方向不是由比率所暗示的; 例如,比率为 2 时生成的矩形的长宽比为 1:2 或者为 2:1(但是,你可以通过在不同的维度上生成一个正方形 treemap 来实现这个结果,然后将 treemap stretching the treemap 到所需的纵横比)。此外指定的长宽比仅仅是一个期望值,实际计算不能保证。如果没有指定的话,默认的纵横比为黄金比例:φ = (1 + sqrt(5)) / 2。
partition layout 用来生成邻接图:一个节点链接树图的空间填充变体。与使用连线链接节点与父节点不同,在这个布局中节点会被绘制为一个区域(可以是弧也可以是矩形),并且其位置反应了其在层次结构中的相对位置。节点的尺寸被编码为一个可度量的维度,这个在节点-链接图中很难表示。
# d3.partition()
使用默认的设置创建一个分区图布局。
对指定的 root hierarchy 进行布局,root 节点以及每个后代节点会被附加以下属性:
- node.x0 - 矩形的左边缘
- node.y0 - 矩形的上边缘
- node.x1 - 矩形的右边缘
- node.y1 - 矩形的下边缘
在将层次数据传递给 treemap 布局之前,必须调用 root.sum。在计算布局之前还可能需要调用 root.sort 对节点进行排序。
如果指定了 size 则将当前的布局尺寸设置为指定的二元数值数组:[width, height],并返回当前 treemap 布局。如果没有指定 size 则返回当前尺寸,默认为 [1, 1]。
# partition.round([round]) <源码>
如果指定了 round 则根据指定的布尔类型值启用或禁用四舍五入,并返回当前 treemap 布局。如果 round 没有指定则返回当前 rounding 状态,默认为 false。
# partition.padding([padding]) <源码>
如果指定了 padding 则设将当前分区布局的间隔设置为指定的数值或函数,并返回当前 partition 布局。如果没有指定 padding 则返回当前的间隔,默认为 0。间隔用于分离节点的相邻子节点。
Enclosure(打包) 图使用嵌套来表示层次结构。最里层表示叶节点的圆的大小用来编码定量的维度值。每个圆都表示当前节点的近似累计大小,因为有空间浪费以及变形;仅仅只有叶节点可以准确的比较。尽管 circle packing 与 treemap 相比不能高效的利用空间,但是能更突出的表示层次结构。
# d3.pack()
使用默认的设置创建一个打包布局。
对 root hierarchy 进行布局,root 节点以及每个后代节点会被附加以下属性:
- node.x - 节点中心的 x- 坐标
- node.y - 节点中心的 y- 坐标
- node.r - 圆的半径
在传入布局之前必须调用 root.sum。可能还需要调用 root.sort 对节点进行排序。
如果指定了 radius 则将半径访问器设置为指定的函数并返回 pack 布局。如果没有指定 radius 则返回当前半径访问器,默认为 null, 表示叶节点的圆的半径由叶节点的 node.value(通过 node.sum 计算) 得到;然后按照比例缩放以适应 layout size。如果半径访问器不为 null 则叶节点的半径由函数精确指定。
如果指定了 size 则将当前 pack 布局的尺寸设置为指定的二元数值类型数组: [width, height] 并返回当前 pack 布局。如果没有指定 size 则返回当前的尺寸,默认为 [1, 1]。
# pack.padding([padding]) <源码>
如果指定了 padding 则设置布局的间隔访问器为指定的数值或函数并返回 pack 布局。如果没有指定 padding 则返回当前的间隔访问器,默认为常量 0。当兄弟节点被打包时,节点之间的间隔会被设置为指定的间隔;外层包裹圆与字节点之间的间隔也会被设置为指定的间隔。如果没有指定 explicit radius(明确的半径),则间隔是近似的,因为需要一个双通道算法来适应 layout size:这些圆首先没有间隙;一个用于计算间隔的比例因子会被计算;最后,这些圆被填充了。
# d3.packSiblings(circles) <源码>
打包指定的一组 circles,每个圆必须包含 circle.r 属性用来表示圆的半径。每个圆会被附加以下属性:
- circle.x - 圆中心的 x- 坐标
- circle.y - 圆中心的 y- 坐标
这些圆是根据 Wang et al. 等人的算法来定位。
# d3.packEnclose(circles) <源码>
计算能包裹一组 circles 的 smallest circle(最小圆),每个圆必须包含 circle.r 属性表示半径,以及 circle.x 以及 circle.y 属性表示圆的中心,最小包裹圆的实现基于 Matoušek-Sharir-Welzl algorithm。(也可以参考 Apollonius’ Problem)