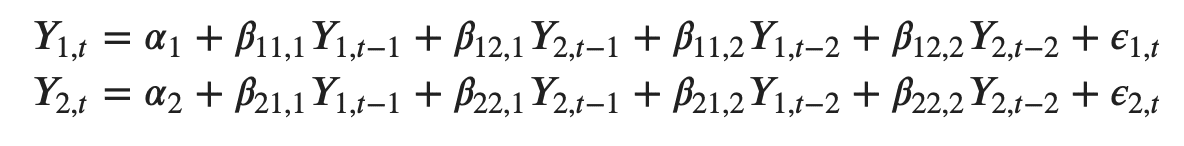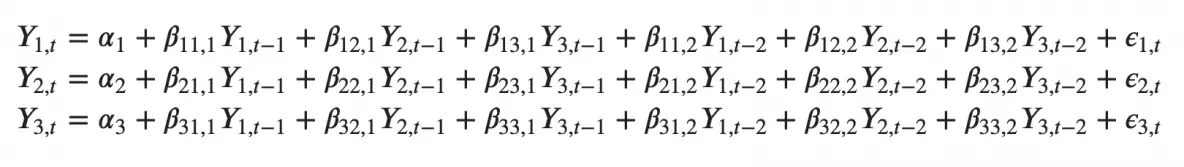Vector Autoregression (VAR) is a multivariate forecasting algorithm that is used when two or more time series influence each other. That means, the basic requirements in order to use VAR are:
You need at least two time series (variables) The time series should influence each other. Alright. So why is it called ‘Autoregressive’?
It is considered as an Autoregressive model because, each variable (Time Series) is modeled as a function of the past values, that is the predictors are nothing but the lags (time delayed value) of the series.
Ok, so how is VAR different from other Autoregressive models like AR, ARMA or ARIMA?
The primary difference is those models are uni-directional, where, the predictors influence the Y and not vice-versa. Whereas, Vector Auto Regression (VAR) is bi-directional. That is, the variables influence each other.
If you remember in Autoregression models, the time series is modeled as a linear combination of it’s own lags. That is, the past values of the series are used to forecast the current and future.
A typical AR(p) model equation looks something like this:
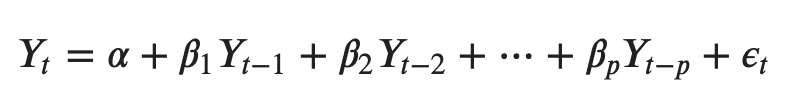
Order ‘p’ means, up to p-lags of Y is used and they are the predictors in the equation. The ε_{t} is the error, which is considered as white noise.
Alright. So, how does a VAR model’s formula look like?
In the VAR model, each variable is modeled as a linear combination of past values of itself and the past values of other variables in the system. Since you have multiple time series that influence each other, it is modeled as a system of equations with one equation per variable (time series). That is, if you have 5 time series that influence each other, we will have a system of 5 equations.
Well, how is the equation exactly framed?
Let’s suppose, you have two variables (Time series) Y1 and Y2, and you need to forecast the values of these variables at time (t).
To calculate Y1(t), VAR will use the past values of both Y1 as well as Y2. Likewise, to compute Y2(t), the past values of both Y1 and Y2 be used.
For example, the system of equations for a VAR(1) model with two time series (variables Y1 and Y2) is as follows:
Where, Y{1,t-1} and Y{2,t-1} are the first lag of time series Y1 and Y2 respectively.
The above equation is referred to as a VAR(1) model, because, each equation is of order 1, that is, it contains up to one lag of each of the predictors (Y1 and Y2).
Since the Y terms in the equations are interrelated, the Y’s are considered as endogenous variables, rather than as exogenous predictors.
Likewise, the second order VAR(2) model for two variables would include up to two lags for each variable (Y1 and Y2):
Can you imagine what a second order VAR(2) model with three variables (Y1, Y2 and Y3) would look like?
As you increase the number of time series (variables) in the model the system of equations become larger.
Analyze the time series characteristics
Test for causation amongst the time series
Test for stationarity
Transform the series to make it stationary, if needed
Find optimal order (p)
Prepare training and test datasets
Train the model
Roll back the transformations, if any.
Evaluate the model using test set
Forecast to future