Uses Python's Pandas library and scikit-learn to predict the rating of a Board game using a dataset of board game statistics
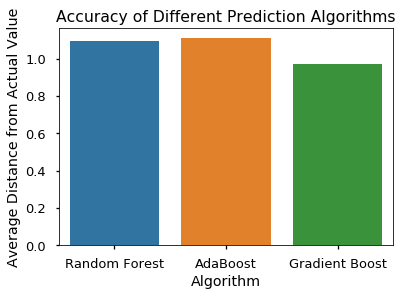
I decided to try 3 different algorithms to predict the data: Random Forest, AdaBoost, and Boosted Gradient Descent. I used cross-validation to check the errors of each algorithm and plotted the results below.
The plot represents how far off the predicted value was from the actual value on average. Boosted Gradient Descent was the best predictor, but was still had a large amount of error.
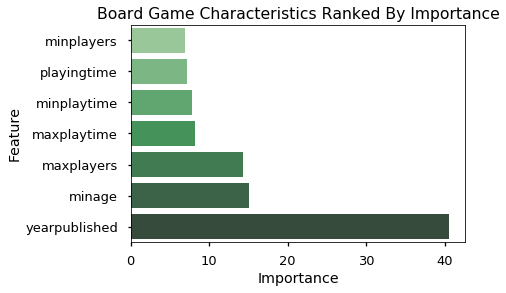
In order to find out why my predictions had so much error, I plotted the importance of each characteristic using the feature importances of the Random Forest I created earlier.
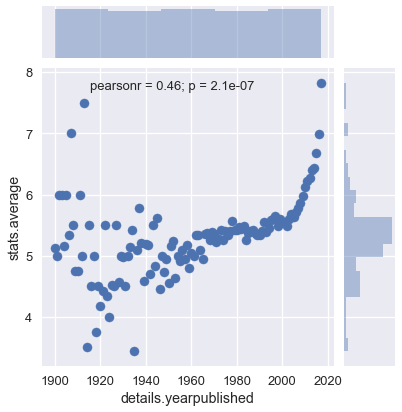
We can easily see that the year a game was published is vastly more important than any of the other characteristics. In order to get a better idea of how exactly publication date and rating were correlated, I plotted them.
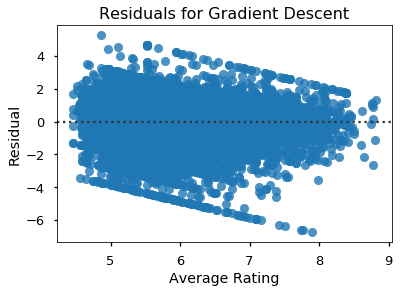
Finally, I wanted to see if there were any ways to improve my Gradient Descent algorithm, so I created a residual plot.
There is a slight negative correlation between the residual and the predicted value, which indicates that there is room for improvement in the algorithm. By varying the hyper-parameters, I should be able to improve the predictions.
The most obvious thing about this plot at first glance is the difference in how the data is distributed. The earlier the year published, the more spread out the data is. This may be due to bias in the data, but without another dataset to check this against, I can't verify that. There seems to be a general trend for the ratings of games to increase starting in the year 2000. It grows extremely quickly, with the average rating jumping from about 5.5 to nearly 8 from 2000 to 2017. From this, I can conclude that people tend to prefer newer games over older ones.
There seems to be very little correlation between the quantifiable characteristics of a board game and its overall rating. The only exception to this rule is the year the game was published, as people prefer more recent games over older ones. Because of this, any prediction algorithms will have limited success. All 3 of the prediction algorithms I tried had similar results, but none of them were very accurate.